





 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|
 |
 |
 |
|---|---|---|
Tbe best way to deflect an asteroid is with a hydrogen bomb. No other device comes close in terms of energy per mass. To defend against asteroids we should have a rocket with a hydrogen bomb in Earth orbit ready to go if an asteroid is found. We also need wide-angle telescopes for detecting asteroids, such as the Pan-STARRS and LSST telescopes.
 |
 |
 |
|---|---|---|
The goal is to maximize the momentum delivered to the asteroid by the bomb, which is equivalent to ejecting as much mass as possible from the asteroid.
A bomb delivers a recoil momentum to an asteroid equal to:
Bomb energy = E Mass ejected by the bomb = M Momentum given to the asteroid = Q = (2 M E)½
At fixed energy, you want to eject as much mass as possible. If you have enough time to land on the asteroid then you should bury the bomb as deep as possible. If you don't, then you have to settle for putting the bomb on a glancing collision course with the asteroid and detonate it just before it hits. The mass ejected can be increased by hitting the asteroid with a pre-impactor, to launch material into space which is then heated by the bomb. The momentum imparted is:
Bomb mass = m Mass ejected = M Pre-impactor effectiveness = f = M/m Bomb energy = E Bomb energy/mass = e = E/m = 2⋅1013 Joules/kg Asteroid recoil momentum = Q = (2 M E)½ = (2 f e)½ m
In the film "Armageddon", an asteroid is on collision course with the Earth and the astronauts deflected it with a hydrogen bomb. The scientists unnecessarily bickered over if it was better to detonate the bomb on the surface or underground.
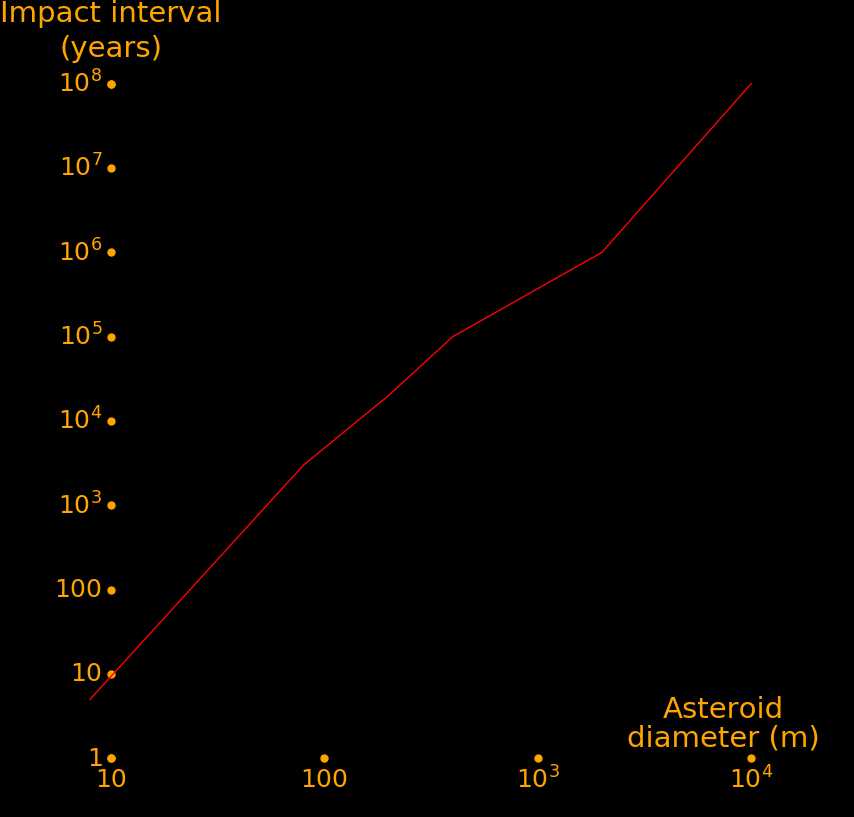
The smallest asteroid capable of penetrating the atmosphere is 50 meters. Such an asteroid has the energy of a 10 Megaton fusion bomb. The minimum for creating a megatsunami is 200 meters. The LSST telescope will find all 200 meter and larger asteroids that are in near-Earth orbits, and hydrogen bombs can redirect any that will impact the Earth. For asteroids from more distant regions of the solar system it won't find them soon enough to deflect them. For this we need more powerful telescopes.
The following table shows impact damage as a function of asteroid size.
Asteroid Energy Tsunami Crater Impact Equivalent energy
diameter height diameter interval
meters EJoules meters km years
8 .0001 0 0 5 Fission bomb, 25 kton TNT equivalent
80 .100 0 1 3000 Fusion bomb, 25 Mton TNT equivalent
200 1 10 3 20000 Krakatoa Volcano, 1883
400 10 20 5 100000 Mag 9.5 quake. Chile, 1960.
2000 1000 200 40 1000000 Hurricane
10000 100000 4000 200 100000000 Asteroid that killed the dinosaurs
1 EJoule = 1018 Joules.
 |
|---|
The Pan-STARRS telescope specializes in finding asteroids. It has a wide field of view and takes short exposures, allowing it to cover the entire sky in 8 days. The upcoming Large Synaptic Survey Telescope (LSST) will cover the sky every 2 days.
Telescope Diameter Field of Exposure Sky survey Year
(meters) view (deg) (seconds) time (days)
Pan-STARRS 3 3.0 60 8 2010 Hawaii
LSST 8.4 3.5 15 2 2021 El Penon, Chile
Flux limit Magnitude
(Watts/m2) limit
Human eye 3e-11 7
Pan-STARRS 5e-18 24
LSST 2e-18 25
Keck 10 meter 1e-19 28
Hubble 1e-20 31
Webb 5e-22 34
 |
|---|
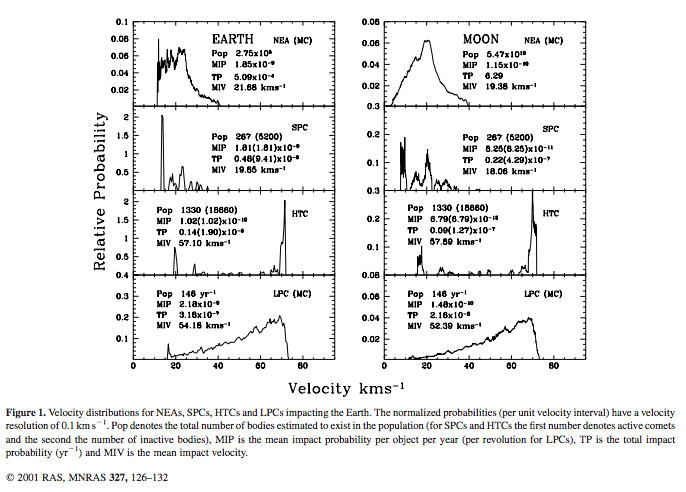
Near Earth asteroids (NEA) approach the Earth at a characteristic speed of ~ 20 km/s. Retrograde comets can approach the Earth as fast as 75 km/s.
NEA: near Earth asteroids SPC: short period comets HTC: Halley-type comets LPC: long period comets"Near-Earth object velocity distributions and consequences for the Chicxulub impactor" S. V. Jeffers, S. P. Manley, M. E. Bailey, D. J. Asher, Mon. Not. R. Astron. Soc. 327, 126–132 (2001)
The largest single-stage fusion bombs have an energy in the range of 25 ktons TNT equivalent. Larger bombs can be made with 2-stage desgins but they have similar energy/mass as a single-stage bomb.
Energy of a large fusion bomb= E = = 1017 Joules = 25 MTons TNT equivalent Mass of a large fusion bomb = M = =4000 kg Fusion bomb energy/mass = e = E/M = 25 TJoules/kg = 6 kTons TNT equivalent per kg TNT energy/mass = z = = 4.2 MJoules/kg
If a bomb is detonated at the center of an asteroid, the bomb energy needs to exceed a critical value to shatter the asteroid, otherwise the asteroid will recollapse gravitationally. The minimum energy required to overcome the asteroid's gravity is:
Asteroid mass = M Gravity constant = G = 6.67⋅10-11 Joule meter / kg2 Asteroid radius = R = 12.9 km Asteroid density = D = M/(4/3 π R3) = 2000 kg/meter3 Gravity energy = E = 3/5 G M2 / R = 16/15 π2 G D2 R5 Bomb energy = Eb = 1017 Joules = 25 MTons TNT equivalent
If the bomb energy exceeds this energy then the asteroid shatters and the speed V of departing shrapnel is:
E = ½ M V2
If a bomb is detonated at the center of an asteroid and if it has enough energy to overcome the asteroid's gravity, the asteroid will shatter and the shrapnel will exit the asteroid at some speed V. This speed has to be large enough so that the shrapnel doesn't hit the Earth. If an asteroid is on a head-on collision course with the Earth,
Earth radius = R = 6.371e6 meters Shrapnel speed = V Time to collision = T = R/V
Departure from the Earth is done with the Oberth maneuver, which uses the Earth to amplify a rocket impulse. The Oberth maneuver is executed by starting the rocket in an elliptical orbit with the perigee as close to the Earth as possible, and the rocket is fired at perigee. Example numbers:
Earth escape speed = Ve = 11.2 km/s Rocket speed change = Vr = 6 km/s Earth departure speed = Vd = (Vr2 + 2 Vr Ve)½ = 13 km/s
A substantial fraction of an asteroid's kinetic energy goes into heating the atmosphere. An asteroid 10 km or larger heats the atmosphere enough to cause a mass extinction, such as what happened to the dinosaurs.
Heat capacity of air = 1.0 Joules/kg/Kelvin
Mass of atmosphere = 5.1 kg
Mass of asteroid Speed of asteroid
Heating ~ 40 kelvin * ---------------- * ( ----------------- )^2
10^15 kg 20 km/s
A 10 km asteroid has a mass of 1015 kg.
Q = Radius of closest approach / Radius of Earth
Q Diameter Date Energy
(meters) (Mtons TNT)
Chelyabinsk 1.0 19 2013 .44
Tunguska 1.0 50 1908 12 Flattened a forest
Arizona asteroid 1.0 50 -50000 10 1 km crater
1972 Fireball 1.0089 ~ 6 1972 Skimmed the upper atmosphere
2011-CQ1 1.87 1 2011
2008-TS26 1.96 1 2008
2011-MD 2.94 10 2011
2012-KT42 3.26 ~ 7 2004
Apophis 4.9 325 2029 510
2013-DA14 5.35 30 2013
2012-KP24 8.99 25 2004
2012-BX34 10.3 8 2012
2012-TC4 14.9 17 2012
2005-YU55 60.00 400 2005
 |
|---|
A cannon provides an example calculation.
Energy = E Mass = M Velocity = V Momentum = Q = M VMomentum conservation:
Mcannon Vcannon = Mball Vball Eball / Ecannon = MballVball2 / (McannonVcannon2) = Mcannon / MballIf we assume that the cannon is vastly heavier than the ball then
Mball << Mcannon Eball >> EcannonThe cannonball gets all the energy.
E = .5 Mball Vball2The momentum of the recoiling cannon is
Qcannon = Mball Vball = (2 Mball E)1/2For fixed gunpowder energy, cannon recoil increases with cannonball mass. This suggests that if you want to deflect an asteroid by detonating a hydrogen bomb that you should arrange for as much material to be ejected from the asteroid as possible. If you can land on the asteroid then you want to bury the bomb before detonating it. If you can't land on the asteroid then you can arrange for an impactor to eject material before detonating the bomb.
 |
|---|