





 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|
 |
 |
 |
 |
 |
||||
|---|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
|||||
|---|---|---|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
||||||
|---|---|---|---|---|---|---|---|---|---|---|
 |
|---|
 |
|---|
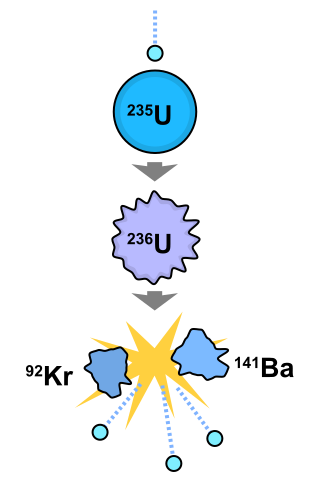
Solar system exploration begins with lunar ice, which can be used for rocket fuel, life support, and radiation shielding. The moon's low gravity makes it easy to launch ice into space. Lunar ice is converted into hydrogen + oxygen rocket fuel, moved to low-Earth-orbit, and used to help rockets go from there to other destinations. Article.
 |
|---|
The future of rocket launch is air launch, giving the rocket a speed boost from the aircraft. Launching at high altitude also reduces air drag. Launch cost is presently $2000/kg and air launch will reduce this. Article.
 |
|---|
In the future, interplanetary travel will be dominated by fission thermal hydrogen rockets, which have a faster exhaust speed than chemical rockets. In a thermal hydrogen rocket, a nuclear reactor or a solar mirror heats hydrogen exhaust. Article.
 |
|---|
Ion drives use electricity to accelerate ions, with electricity coming from nuclear power. Article.
 |
|
|---|---|
The best place for telescopes is the Lagrange point L2. A base will be built here and colossal telescopes will be assembled on site. Article.
 |
|
|---|---|
Metallic asteroids contain trillions of dollars of platinum group metals. They can be mined and moved with space mirrors. Article.
 |
 |
 |
 |
 |
 |
|||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
The rockets that are possible with current technology are:
Chemical React chemicals, for example hydrogen + oxygen Thermal hydrogen Hydrogen exhaust is heated with nuclear or solar power Ion rocket Accelerate ions, powered by electricity from nuclear or solar Fusion bomb rocket Can move large objects like asteroids Fission afterburner Neutrons trigger fission in the exhaust Alpha rocket A radioisotope emits alpha particles as exhaust
 |
|---|
Chemical H2+O2, Kerosene+O2, or solid fuel (Al+NH4NO3) Fission Uranium-235, Plutonium-239, Americium-242m, Beryllium-7 Radioactivity Plutonium-238, Cobalt-60, Lead-210 Solar Photovoltaic cells or solar mirror heat Fusion A fusion bomb using Deuterium + Lithium-6
The maximum exhaust speed is given by the energy/mass of the energy source.
Exhaust speed = V Energy/Mass = e = ½ V2
This is the "perfect" exhaust speed. In practice the exhaust speed is less.
Energy Practical Perfect Energy/Mass
source exhaust exhaust
speed speed
km/s km/s MJoule/kg
Fusion Deuterium+Li6 6900 23000 270000000
Fission Uranium-235 4000 12000 74000000
Fission Plutonium-239 4000 12000 76000000
Radioactive Plutonium-238 50 2100 2300000
Chemical Hydrogen+O2 4.4 5.1 13.2
Chemical Methane +O2 3.7 4.7 11.1
Chemical Kerosene+O2 3.3 4.5 10.3
Chemical Al+NH4NO3 2.7 3.7 6.9
 |
|---|
The relationship between rocket quantities is:
Exhaust speed = V Exhaust energy/mass = e = ½V2 Exhaust power/mass = p = ½V2/T = e/T Burn time = T Acceleration = A = 2p/V = V/T
"Burn time" is the time for a rocket to expel its own mass of propellant. The shorter the burn time the better.
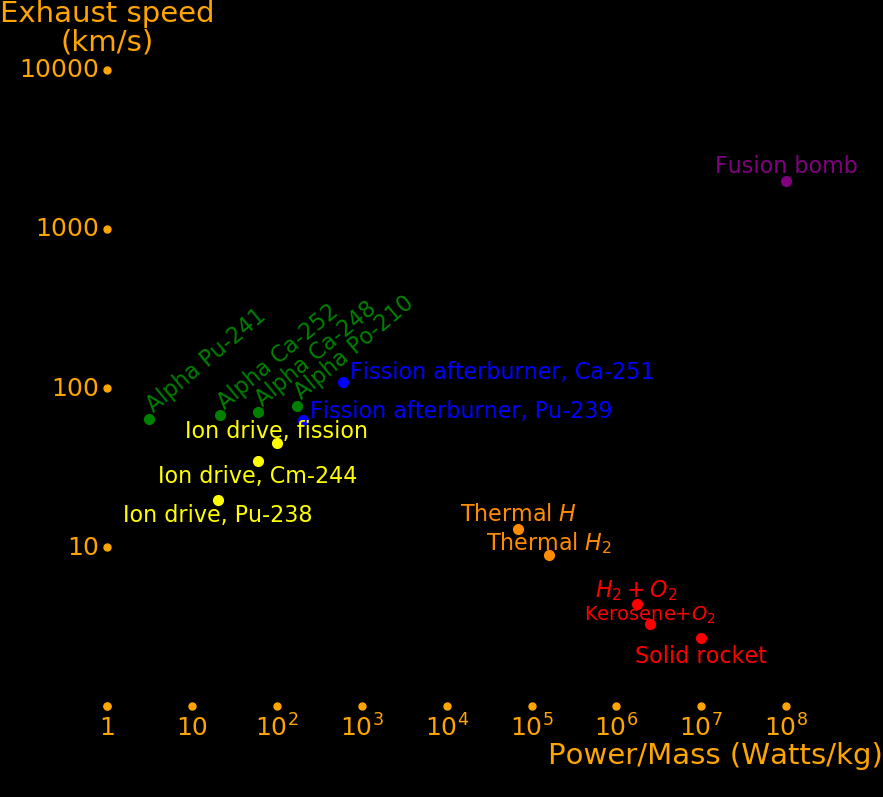
For ion drives the exhaust speed is customizable. The power/mass is fixed and there is a tradeoff between exhaust speed and acceleration. In the table below we choose a burn time of 107 seconds (3 months) for ion rockets.
It is difficult to make a rocket with both large power/mass and large exhaust speed. Fusion bombs qualify but they can only be used to move large objects like asteroids.
Rocket type Exhaust Power/Mass Acceleration Burn time
km/s Watts/kg meters/s/s seconds
Chemical, Hydrogen+O2 4.4 1700000 770 5.6
Chemical, Methane +O2 3.7 2500000 1350 2.7
Chemical, Kerosene+O2 3.3 5000000 3030 1.1
Chemical, Al+NH4NO3 2.5 9000000 7200 .3 Solid fuel
Fission thermal H2 9 160000 36 253 A fission reactor heats H2
Fission thermal H 13 70000 11 1200 A fission reactor heats atomic hydrogen
Ion drive 45 100 .0045 10000000
Fission afterburner, Am-242m 93 200 .0043 22000000
Fission afterburner, Pu-239 30 200 .013 2200000
Fission afterburner, Be-7 134 200 .0030 45000000
Fission afterburner, He-3 40 200 .010 4000000
Fission afterburner, Li-6 31 200 .013 2400000
Fission afterburner, B-10 35 200 .011 3100000
Alpha, Po-210 77 171 .0016 12000000 Half life .38 years
Alpha, Ca-248 71 60 .002 28700000 Half life .91 years
Alpha, Ca-252 68 19 .00019 82000000 Half life 2.6 years
Alpha, Pb-210 77 2.9 .000075 730000000 Half life 22.3 years
Alpha, U-230 200 7000 Half life .0554 years
Alpha, Th-228 180 170 .0019 62000000 Half life 1.91 years
Alpha, Ra-228 180 57 .00063 190000000 Half life 5.75 years
Alpha, Ac-227 180 15 .00017 710000000 Half life 21.8 years
Alpha, U-232 200 5.7 Half life 68.9 years
Fission bomb Large Large Large Short
Fusion bomb Large Large Large Short Deuterium + Lithium-6
Solar sail 300000 228000 .00152
 |
 |
 |
 |
|
|---|---|---|---|---|
The chemical rocket with the fastest exhaust is hydrogen+oxygen (HOX). It is the most expensive chemical rocket because hydrogen has to be liquefied at 20 Kelvin. Because the liquid hydrogen has low density, HOX can't be used for the first stage of a ground rocket, but it can be used for upper stages. HOX is easy in space.
Kerosene is often used because it's liquid at room temperature. Methane is slightly better than kerosene but it must be stored as a liquid at 112 Kelvin.
Solid fuel is cheap, simple, and reliable, and is often used for the first stage.
Fuel Exhaust Fuel Fuel boiling
speed density point
(km/s) (g/cm3) (K)
Hydrogen 4.4 .07 20 Complex because of the low boiling point of hydrogen
Methane 3.7 .42 112 New technology pioneered by SpaceX
Kerosene 3.3 .80 410 Simple because kerosene is a liquid at room temperature
Solid fuel 2.7 1.2 - Simple and cheap. Often Aluminum + NH4NO3
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|
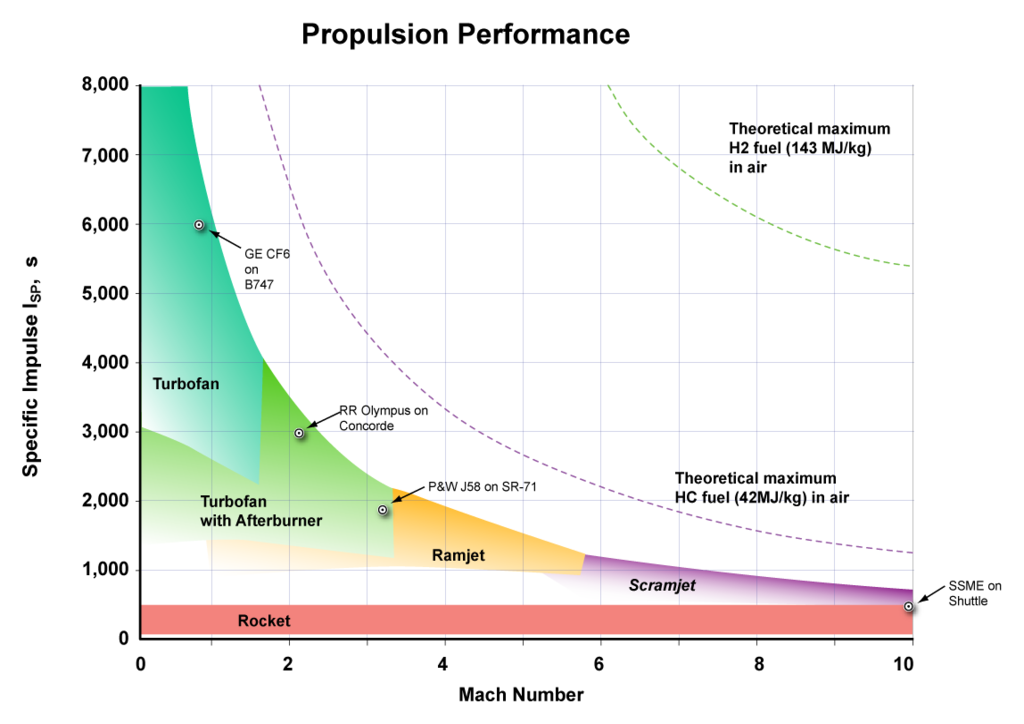
In air launch, an aircraft launches a rocket at high altitude. Air launch has advantages over ground launch, such as:
*) The aircraft speed adds to the rocket speed.
*) Less air drag. Air at 15 km has 1/4 the density of air at sea level.
*) The rocket can be launched at the equator so that the Earth's equatorial speed adds to the rocket speed.
*) Ramjet launch makes it possible to reach orbit with cheap solid rockets.
Speed Speed
(km/s) (Mach)
Earth rotation at equator .46 1.6
Turbofan aircraft .27 .9
Ramjet aircraft 1.5 5
Scramjet aircraft >1.5 >5
Solid rocket exhaust 2.7 9
Kerosene rocket exhaust 3.3 11
Hydrogen+Oxygen rocket exhaust 4.4 15
low Earth orbit 7.8 26.4
At present, turbofan aircraft are being built for launching rockets, and in the near future ramjet aircraft will be used. For ramjet launch:
Stage Type Speed increase End speed
km/s km/s
0 Equator motion .45 .45
1 Ramjet 1.55 2.0
2 Solid rocket 4.0 6.0
3 HOX 2.0 8.0 Orbit speed
 |
|---|
 |
 |
|---|---|
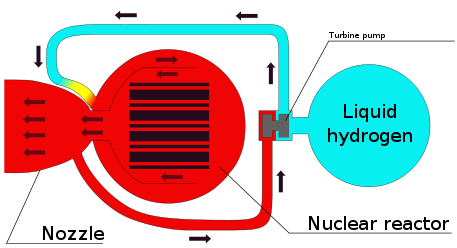
A fission thermal hydrogen rocket uses fission to heat hydrogen propellant. It has a higher exhaust speed than chemical rockets (13 km/s vs. 4 km/s).
In a chemical rocket the energy comes from a chemical reaction and this puts an upper limit on the exhaust speed. Reacting hydrogen and oxygen gives an exhaust speed of 4.4 km/s. Nuclear power can reach higher exhaust speed.
Rocket type Exhaust speed (km/s) Nuclear Fission thermal H 13 Nuclear Fission thermal H2 9 Chemical Hydrogen + Oxygen 4.4 Chemical Methane + Oxygen 3.7 Chemical Kerosene + Oxygen 3.3 Chemical Solid fuel 2.7
Hydrogen is used for its low mass. The lower the mass of the propellant molecule, the higher the exhaust speed.
Exhaust speed is determined by temperature. For a temperature of 2750 Kelvin, the speed of monatomic hydrogen propellant is 13 km/s.
Monatomic hydrogen mass= M =1.66⋅10-27 kg Temperature = T = 2750 Kelvin Exhaust speed = V = 13 km/s Boltzmann constant = k =1.38⋅10-23 Joules/Kelvin Exhaust constant = K = ½ M V2 / (1.5 k T) = 2.46
At 2750 Kelvin,
Molecule Mass Exhaust speed
AMU km/s
H 1 13.0
H2 2 9.2
H2O 18 3.1
H2 dissociates into atomic H at high temperature and low density. A thermal rocket has two modes: use H2, which has high pressure and high power/mass, or use H, which has low pressure and low power/mass. The low-pressure mode still has enough power/mass to propel humans to the outer planets.
In a mirror rocket, a space mirror focuses sunlight onto hydrogen propellant.
The fission material with the highest melting point is uranium oxide, which melts at 3138 Kelvin. Achieving a higher temperature requires liquid fission fuel that's embedded in a material with a higher melting point. The materials with the highest melting points are:
Melt Boil
Kelvin Kelvin
HfCN 4400
Ta4HfC5 4263
Hafnium carbide HfC 4201
Tantalum carbide TaC 4150
Niobium carbide NbC 3881
Zirconium carbide ZrC 3805 5370
Carbon (graphite) 3800
Tungsten 3695 6203
 |
|---|
A thin film mirror can focus sunlight and heat hydrogen. The power/mass of the rocket is limited by the power/mass of the mirror. JPL designed a mirror with the goal of minimizing mass/area.
Solar flux = f = 1365 Watts/meter2 Mirror mass/area = d = .006 kg/meter2 Mirror power/mass = p = f/d =228000 Watts/kg
The mirror consists of mylar coated with aluminum.
Mylar density = 1.39 g/cm3 Aluminum density = 2.70 g/cm3 Mylar thickness = .025 mm Aluminum thickness = .010 mm
 |
|---|
An ion drive uses electric power to accelerate ions. Electric power can come from nuclear fission, radioactivity, or solar cells. The ion speed is customizable. It should be at least as large as 20 km/s otherwise you might as well use a chemical or thermal rocket. The upper limit is given by the mission duration. We calculate the ion speed assuming a Plutonium-238 heat source and a burn time of 107 seconds.
Heat source Power/Mass = P = 567 Watts/kg Plutonium-238 Electrical efficiency = D = .05 Convert heat to electricity Drive efficiency = d = .6 Convert electricity to ion energy Electric Power/Mass = p = edP = 28 Watts/kg Burn time = T = 10 Million seconds = 3 months Ion speed = V = (2pT)½ = 24 km/s Ion Energy/Mass = e = pT = 280 MJoules/kg
Power in space is usually limited by cooling. For an electric generator that is closed-cycle and doesn't expel mass, cooling is limited by blackbody radiation and the maximum power/mass is determined by temperature. An example of an open-cycle system is a thermal hydrogen rocket, where the expelled mass serves as coolant and the power/mass can be much higher than for a closed-cycle system.
 |
|---|
The power/mass of solar cells depends on distance from the sun. At the Earth, solar cells have similar power/mass as nuclear, and beyond the Earth, solar cells are worse than nuclear.
Location Power/Mass Distance from sun
Watts/kg AU
Earth 100 1
Mars 43 1.52
Ceres 13 2.77
Jupiter 3.7 5.2
 |
 |
 |
 |
|---|---|---|---|
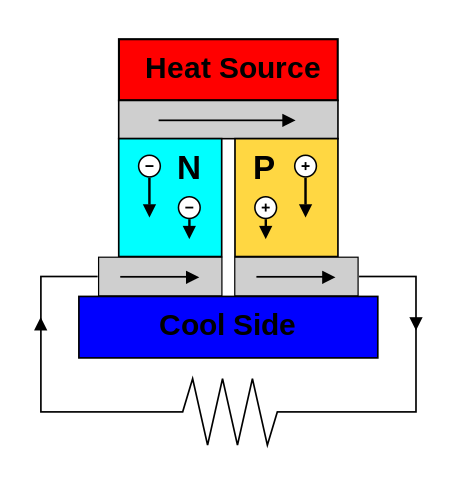
Heat can be converted to electricity with a Stirling engine, a thermoelectric generator, or photovoltaics. Usually the generator and cooling system have more mass than the heat source. Heat comes from fission or radioactivity.
Examples of existing space generators:
Heat source Generator Electricity Heat source Electric Fuel Total
Watts/kg Watts/kg efficiency fraction efficiency
Uranium-235 Brayton 195 .25 SAFE-400 reactor
Uranium-235 Stirling 44 991 .23 .193 .044 Kilopower reactor
Plutonium-238 Thermoelectric 5.3 567 .068 .137 .0093 GPHS-RTG. Galileo and Cassini
Plutonium-238 Thermoelectric 4.2 567 .062 .119 .0074 Voyager 1 and Voyager 2
Plutonium-238 Thermoelectric 2.8 567 .049 MMRTG. Curiosity rover
Features of the Kilopower reactor:
*) Fuel cast as Uranium-Molybdenum alloy. Molybdenum has a melting point of 2896 Kelvin.
*) Beryllium oxide moderator, which has a melting point of 2780 Kelvin.
*) Boron carbide control rods, with a melting point of 3036 Kelvin.
*) Passive cooling with liquid sodium coolant, which melts at 371 Kelvin and boils at 1156 Kelvin.
*) Cannot melt down because the reaction rate decreases with increasing temperature.
*) Stirling engine to convert heat to electricity.
 |
 |
|---|---|
 |
 |
|---|---|
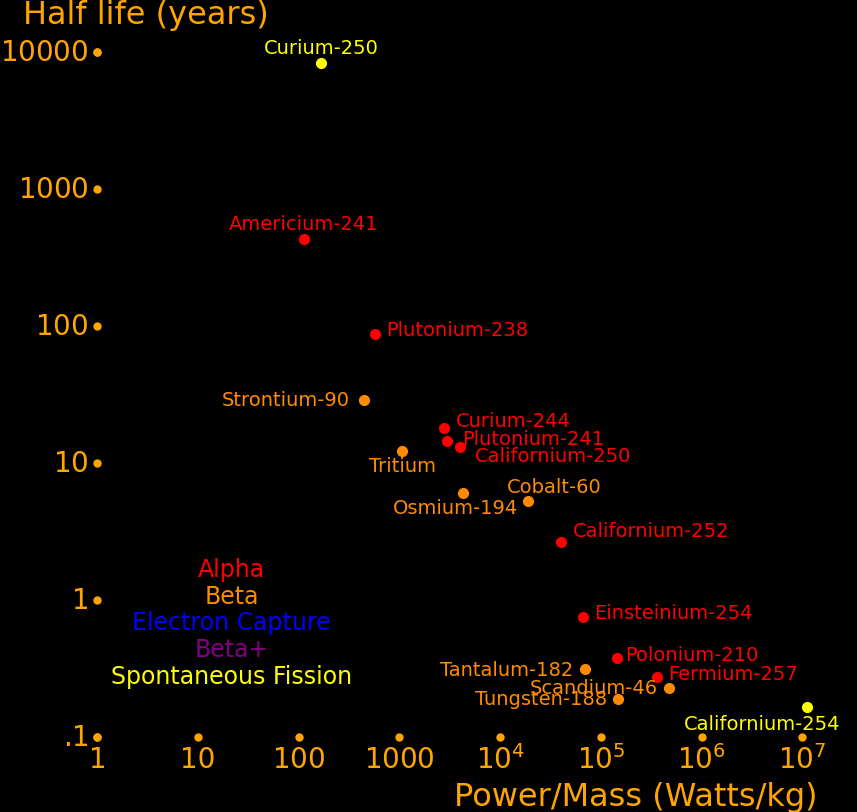
The most important radioactive isotopes for power are:
Plutonium-241 Good balance of power/mass and half life. Easy to produce. Curium-244 Good balance of power/mass and half life. Strontium-90 Abundant because it's present in burnt fission fuel. Polonium-210 Alpha rocket Lead-210 Alpha rocket Thorium-228 Alpha rocket Caesium-137 Abundant because it's present in burnt fission fuel. Plutonium-238 Outperforms Strontium-90. Has to be bred in a reactor. Cobalt-60 Larger power/mass than plutonium-238. Easily produced with neutron transmutation. Scandium-46 Ludicrously high power/mass, and easily produced by neutron transmutation. Californium-252 Superlatively large power/mass. Capable of powering an Iron Man suit. Curium-252 Decays by spontaneous fission 3% of the time Curium-254 Decays primarily by spontaneous fission
Half life Heat Decay Decay Obtainable by
year Watt/kg MeV neutron transmutation
Californium-254 .166 11200000 Fission 207 *
Scandium-46 .229 485000 β 2.366 *
Polonium-210 .379 144000 α 5.41 *
Ruthenium-106 1.023 71200 2β 3.584 *
Californium-252 2.64 41400 α or Fission 12.33 * α 96.9% (6.12 Mev). Fission 3.09% (207 MeV)
Cobalt-60 5.27 19300 β 2.82 *
Osmium-194 6.02 4313 2β 2.330 *
Lead-210 22.3 2907 α 9.100 *
Plutonium-238 87.7 578 α 5.59 *
Americium-242m 141 725 2α 12.33 *
Curium-250 8300 170 Fission 148 * Fission 74%, Alpha 18%, Beta 8%
Beryllium-7 .146 1822000 EC .547
Sodium-22 2.6 68700 β+ or EC 2.842
Uranium-230 .0554 9280000 6α+2&beta
Thorium-228 1.912 235000 5α+2&beta 34.784
Radium-228 5.75 90660 5α+4&beta 40.198
Polonium-208 2.898 α
Actinium-227 21.8 21600 5α+3&beta 36.18
Uranium-232 68.9 7545 6α+2&beta 40.79
Radium-226 1599 286 5α+4&betz 34.958
Thorium-229 7917 57.7 5α+3&beta 35.366
Protactinium-231 32600 16.2 6α+3&beta 41.3
For a heat engine, the higher the temperature, the more efficient. High temperature also means higher radiative cooling power. Isotopes with a high boiling point are:
Half life Heat Decay Decay energy Melt Boil Obtainable by
year Watt/kg MeV Kelvin Kelvin neutron transmutation
Uranium-230 .0554 9280000 6α 1405 4404
Tungsten-188 .191 148700 2Beta 3695 6203 *
Tantalum-182 .313 68866 Beta 3290 5731 *
Tungsten-181 .332 59200 EC 1.732 3695 6203 *
Iridium-194m .468 50400 Gamma 2.229 2719 4403 *
Rhodium-102 .557 67000 Beta+ 2237 3968
Ruthenium-106 1.023 71200 2Beta 3.584 2607 4423 *
Hafnium-172 1.87 11700 EC 1.835 2506 4876
Thorium-228 1.912 235000 5α 34.784 2023 5061
Rhodium-101 4.07 9890 EC 1.980 2237 3968
Osmium-194 6.02 4313 2Beta 2.33 3306 5285 *
Actinium-227 21.8 12000 5α 36.18 1500 3500
Uranium-232 68.9 7545 6α 40.79 1405 4404
Thorium-229 7917 57.7 5α+3&beta 35.366 2023 5061
Protactinium-231 32600 16.2 6α+3&beta 41.33 1841 4300
 |
|---|
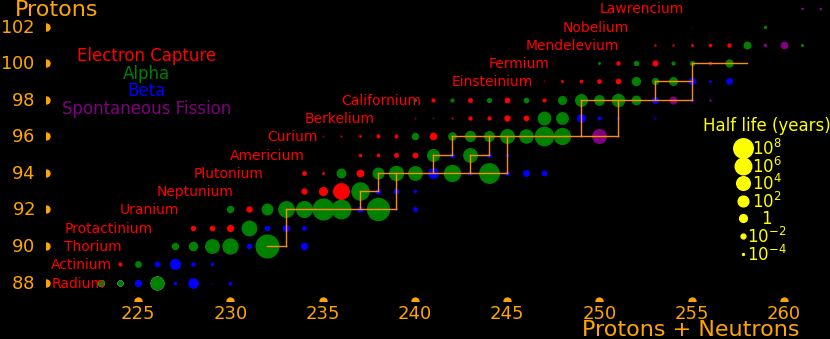
Neutron capture transmutes an isotope one space to the right and beta decay transmutes an isotope one space up.
The most massive nuclei that exist naturally are thorium-232, uranium-235, or uranium-238. All are unstable but have half lives larger than 700 million years. The road starts with these isotopes and then adding neutrons transmutes them according to the orange lines. The road forks at beta isotopes, which can either beta decay or capture a neutron.
The end of the road is fermium. Neutrons can't further increase the proton number because no fermium isotopes on the road beta decay. The road goes as far as fermium-258, which has a half life of .00037 seconds and spontaneously fissions. Producing heavier isotopes requires an accelerator or an extreme neutron flux (such as occurs in a fission bomb).
.svg.png) |
|
|---|---|
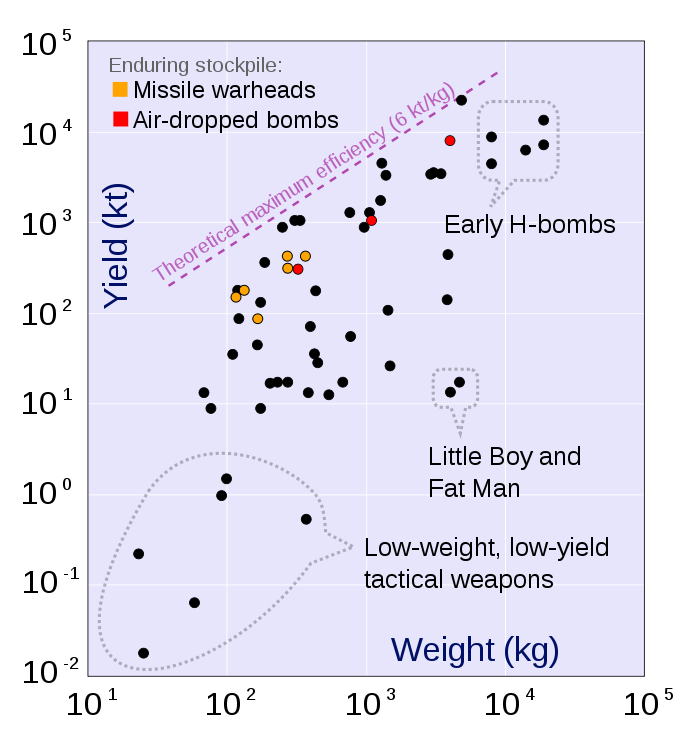
A TRIGA reactor doesn't melt down if the cooling system fails because it's engineered to turn off if it overheats. It's also designed so that adding and removing fuel elements is easy. The reactor is easy to build and can be operated in space.
 |
|---|
Fusion bomb maximum practical yield = = e = 21700 GJoules/kg Mass fraction converted to energy = f = e/C2 =.00072 Exhaust speed = V = (2e)½ = 6588 km/s
Mass is usually added to the bomb to increase momentum and decrease exhaust speed. Or, the bomb is detonated underground in an asteroid, which adds mass.
 |
 |
|---|---|
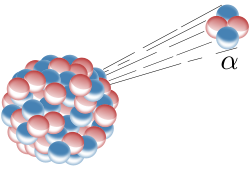
Alpha particles can be used as exhaust. An alpha emitter is coated on a mylar sail, with the coating thin enough so that most of the alphas escape into space. This rocket is simple and can be made arbitrarily small.
The recoil momentum of the nucleus is absorbed by the sail and the recoil speed of the nucleus is the effective exhaust speed. For example, polonium-208 alpha decays to lead-204 and the recoil speed of lead-204 is:
Alpha mass = m = 4 AMU = 6.64⋅10-27 kg lead-204 mass = M = 204 AMU Alpha energy = e = ½ m v2 = 5.22 MeV The alpha gets almost all the kinetic energy Alpha speed = v = (2e/m)½=15871 km/s lead-204 recoil speed = V = vm/M = 311 km/s
The speed calculated is for the most fortunate case where the alpha goes directly aft of the spacecraft. Calculating the average recoil speed involves integrating over all emission directions and accounting for absorption by the emitting material. In the ideal case, all particles emitted in the aft hemisphere escape and all particles emitted in the forward hemisphere are absorbed, in which case the effective recoil speed is 1/4 the fortunate speed. For polonium-208 the effective recoil speed is 78 km/s.
To calculate the power/mass of an alpha rocket,
Speed of projectile = v Speed of emitter (recoil) = V Mass of projectile = m = 4 AMU Mass of emitter = M = 204 AMU Energy of projectile = e = ½mv2 Energy of emitter = E = ½MV2 Momentum of projectile = q Perfect exhaust speed = S = q/M Effective exhaust speed = s = S/4 Effective exhaust energy = g = ½Ms2 Exhaust energy / Decay energy = r = g/e = 16-1 m/M
For a polonium-208 alpha rocket, the power/mass and energy/mass are:
Effective recoil speed = V = 78 km/s Energy/Mass = e = ½V2 =3042 MJoules/kg Half life = T =2.90 years Power/Mass = p = e/t = 33 Watts/kg
The lighter the isotope the larger the recoil speed. Almost all alpha emitters are actinides, the only exceptions being gadolinium-148, polonium-208, polonium-209, and polonium-210. Alpha rockets using actinides have an average recoil speed of ~75 km/s.
The best alpha-emitting isotopes are:
Half life Power/Mass Decay Energy Neutron transmutable
year Watts/kg MeV
Polonium-210 .379 144000 α 5.41 *
Einsteinium-254 .755 105432 α 6.616 *
Californium-248 .91 59760 α 6.36
Californium-252 2.64 21640 α 6.12 *
Polonium-208 2.898 α
Californium-250 13.1 5779 α 6.02 *
Curium-244 18.1 4014 α 5.80 *
Curium-243 29.1 1885 α
Lead-210 22.3 2907 α 9.100 *
Gadolinium-148 70.9 952 α 3.18
Plutonium-238 87.7 578 α 5.59 *
Americium-242m 141 725 2α 12.33 *
Thorium-227 .0512 9194000 6α+2β 36.14
Uranium-230 .0554 9280000 6α+2β
Thorium-228 1.912 235000 5α+2β 34.784
Radium-228 5.75 90660 5α+4β 40.198
Actinium-227 21.8 21600 5α+3β 36.18
Uranium-232 68.9 7545 6α+2β 40.79
Radium-226 1599 286 5α+4β 34.958
Thorium-229 7917 57.7 5α+3β 35.366
Protactinium-231 32600 16.2 6α+3β 41.33
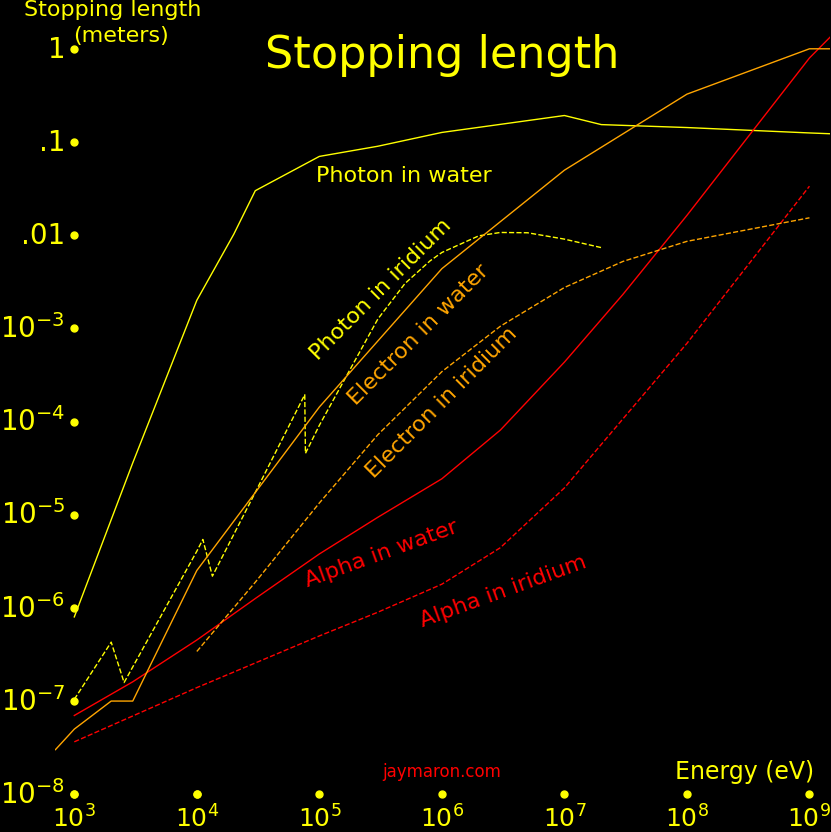
A charged particle passing through matter loses energy from collisions with electrons, with the energy loss rate given by the Bethe formula. For an alpha particle passing through water,
Particle energy = E = 6 MeV Particle mass = M = 4 AMU Particle charge = Z = 2 Proton charges Material density = D = 1000 g/cm2 Stopping distance = X = EZ-2M-1D-1C = .049 meters (Inputs in MeV, AMU, and g/cm3. Output in meters) Material stopping constant = C =.000131 Stopping power = S = 778000 MeV meter2 Mass/Area = m = DX = .049 kg/meter2
SpaceX has the world's lowest launch cost at $2300, and they lead the world for material launched to orbit.
SpaceX pioneered the methane engine, which has a higher exhaust speed (3.7 km/s) than traditional kerosene engines (3.1 km/s). The SpaceX methane engine also has a mighty thrust/weight of 200, the highest of any rocket. This means fewer engines are needed, saving on cost.
SpaceX pioneered recycling the engines in the first rocket. The engines are 35% of the rocket cost and hence worth saving.
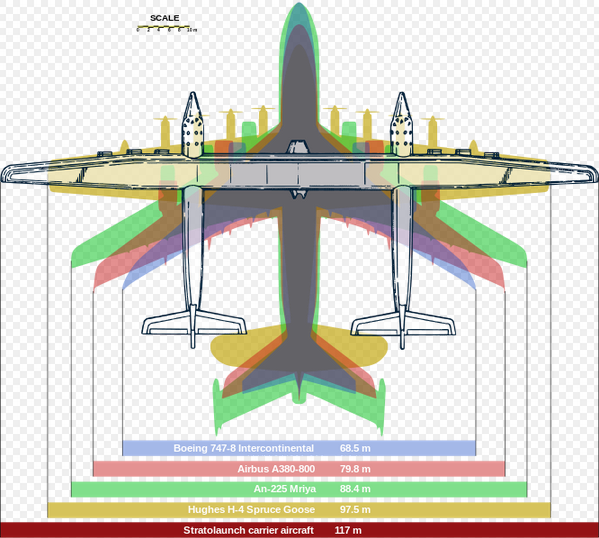
SpaceX once teamed up with Stratolaunch to do air launch, but then SpaceX backed out. Stratolaunch has yet to produce a working launch platform.
 |
 |
 |
 |
|---|---|---|---|
SpaceX has the world's lowest launch cost at $2300, and they lead the world for material launched to orbit. The table shows the total payload launched to orbit in 2020. SpaceX outlaunches NASA and China. SpaceX also has no fails from 2020.
Payload Successes Fails
tons
America SpaceX 286 26 0 Elon Musk
China CNSA 242 31 2
America NASA 103 10 0
Russia Roscosmos 80 16 0
Europe ESA 27 4 1
Japan JAXA 8 4 0
America Orbital 7 2 0
India ISRO 2 2 0
Canada CSA 1 3 0
America Rocket Lab .7 6 1 Peter Beck
America Blue Origin 0 0 0 Jeff Bezos
America Stratolaunch 0 0 0 Paul Allen and Burt Rutan
S Korea KARI 0 0 0
America Virgin Orbit 0 0 0 Richard Branson
SpaceX pioneered the methane engine, which has higher exhaust speed than kerosene.
For the SpaceX Falcon 9 rocket, the engines are 35% of the cost and hence worth saving. SpaceX pioneered recyling the first rocket stage. For a Falcon 9 rocket,
 |
|---|
A fission afterburner uses fission fuel as exhaust, with fission triggered by neutrons from a reactor.
The reactor operates in pulse mode. The reactor produces a pulse of neutrons that trigger fission in the fuel, and then the fuel is expelled. The reactor then has to cool down before generating another pulse.
A TRIGA-style reactor can produce millisecond neutron pulses. The pulse is initiated by neutrons from spallation, where high-energy protons from an accelerator strike a tungsten target and eject neutrons from tungsten nuclei. Fuel can be confined magnetically for the duration of the pulse.
Fission fuel should have a large fission cross section for thermal neutrons, and the best isotopes are:
Half life Fission Energy Quality Exhaust Neutron capture
year barn MeV meter/s output
Americium-242m 141 7024 195 5640 93 Daughter nuclei + Neutrons
Californium-251 900 4801 207 3940 78 Daughter nuclei + Neutrons
Curium-245 8500 2161 198 1740 52 Daughter nuclei + Neutrons
Plutonium-239 14100 748 189 590 30 Daughter nuclei + Neutrons
Uranium-235 704000000 538 181 410 25 Daughter nuclei + Neutrons
Beryllium-7 .146 56800 1.644 11670 134 Lithium-7 + Proton
Helium-3 Stable 5333 .764 1020 40 Tritium + Proton
Boron-10 Stable 3835 2.34 820 35 Lithium-7 + Alpha
Lithium-6 Stable 940 4.783 640 31 Alpha + Tritium
Fuel quality is given by:
Neutron capture cross section = A meter2 At 300 Kelvin Fission energy = E Joule Mass = M kg Mass of target + mass of neutron Fuel quality = Q = AE/M
Neutrons are chilled to liquid helium temperature before encountering the fuel, to increase the neutron capture cross section. Cross sections in the table are for 300 Kelvin.
The exhaust speed is:
Room temperature = T = 300 Kelvin Helium boiling point = t = 4.2 Kelvin Neutron chill factor = C = (T/t)½ = 8 Dimensionless Neutron capture cross section at 300 Kelvin= A meter2 Neutron capture cross section at 4 Kelvin = CA meter2 Neutron number density = n = 1019 neutrons/meter2 Target number density = N = 1/A Nuclei/meter2 Number density of fuel nuclei Fraction of targets that capture neutrons = F = n/N Exhaust energy/mass = e = CFE/M = CnAE/M Exhaust speed = V = (2e)½
The fuel number density should be large enough to capture most of the neutrons, and not larger, and this corresponds to "tA=1". At this density, most neutrons are captured. Only a small fraction of targets get neutrons. There are never enough neutrons to fission all the fuel, hence the goal is to maximize neutron density.
The fission reactor produces a neutron pulse with a density of order 1019 neutrons/meter2 and timescale of order 1 millisecond. During the pulse, the uranium in the reactor heats up by of order 3500 Kelvin. We assume 1 ton of uranium. The reactor pulse is initiated by a pulse of neutrons from spallation.
Uranium melting point = 1405 Kelvin Uranium boiling point = 4404 Kelvin Uranium melt energy = 38900 Joule/kg Uranium heat capacity = 118 Joule/kg Uranium temperature change = 3500 Kelvin Uranium heat energy change per mass = .413 MJoule/kg Uranium heat per neutron = 200 MeV/neutron Neutrons per kg of uranium = 2.6e16 Neutrons/kg Uranium mass = 1000 kg Neutrons in the pulse = 2.6e19 Neutrons Uranium density = D = 17300 kg/meter3 (liquid) Uranium radius = .24 meter Inner sphere Reactor radius = .4 meter Includes an outer shell of moderator Neutron density = 1.3e19 Neutrons/meter3
The rocket consists of concentric spherical shells, with shell 1 the innermost.
Shell 1: Contains the nuclear reactor that generates neutrons.
Shell 2: Beryllium oxide moderator to slow neutrons to room temperature.
Shell 3: Liquid helium moderator to further slow the neutrons
Shell 4: Pressure vessel containing the fission fuel and exhaust gas
Shell 5: Liquid helium moderator to return neutrons back to shell 3.
The more compact the reactor and moderator, the better. The moderator with the largest hydrogen density is TaD5.
The stopping length of a neutron in Americium-242m is:
Cross section = A = 6686 barns Atomic mass unit = u = 1.660e-27 kg Nucleons = q = 242 Nucleus mass = M = 4.02e-25 kg Atom density = N = D/u = 2.99e28 atoms/meter3 Density = D = N u q = 12000 kg/meter3 Neutron stopping length = X = 1/(AN) = 5.00e-5 meters Americium-242m mass/Area= m = D X = .6 kg/meter2
A steel gun can achieve a chamber pressure of 4⋅108 Pascals and a
tungsten gun can achieve a chamber pressure of 109 Pascals.
A solar sail gains momentum from reflecting sunlight. For a solar sail at Earth orbit:
Solar brightness = B = 1365 Watt/meter Speed of light = C = 2.99e8 meter/second Energy delivered in 1 second = E = 1365 Joule Momentum delivered in 1 second = Q =2E/C = 9.1e-6 kg meter/second Mirror mass/area = D = .006 kg/meter2 Acceleration = A = Q/M = .00152 meter/second2 Speed after 1 year = 49600 meter/second Power/mass = P = B/D = 228000 Watt/kg
 |
 |
|---|---|
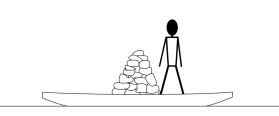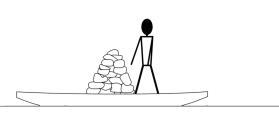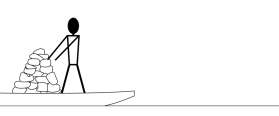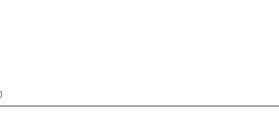
As a rocket burns through fuel it gets lighter. The "Tsoilkovsky rocket equation" relates the final rocket speed to the exhaust speed.
T = Time
M(T)= Mass of rocket as a function of time
Mi = Initial mass of rocket
Mf = Final mass of rocket after burning its fuel
Ve = Rocket exhaust speed
V(T)= Rocket speed as a function of time. V(0)=0.
Vf = Final rocket speed after burning its fuel
F = Force generated by the rocket
= - Ve dM/dT
dV/dT = F/M = -(Ve/M) * dM/dT
V(T) = V ln(Mi/M)
Vf = V ln(Mi/Mf) Tsoilkovsky rocket equation
 |
 |
 |
 |
 |
|---|---|---|---|---|
An electomagnetic launch sled rides on rails like a roller coaster and can reach a speed of 3 km/s. The sled releases a rocket which accelerates to orbit. The cost of the electricity is negligible compared to the cost of the rocket and hence sled launch reduces launch cost compared to ground launch.
If energy were the only contributor to launch cost then launch cost would be tiny. It costs typically 2000 $/kg to launch material into space with rockets. If the kinetic energy comes from electricity then the electricity cost is $1.
Orbit speed = V = 7.8 km/s Cost of electricity = q = 36 MJoules/$ Orbit energy/mass = e = 30 MJoules/kg = ½ V2 Electricity cost/mass = c = .85 $/kg = e/q Typical launch cost = 2000 $/kg Typical cost to use rockets to launch material to orbit
Launch sleds are best suited for inanimate cargo that can handle large acceleration. If an acceleration low enough for humans is used then the track is excessively long. If we use a human-friendly acceleration of 5 g's,
Sled acceleration = A = 50 m/s2 (5 g's. Maximum acceleration for humans) Sled final velocity = V = 3.0 km/s Length of the track = X = 90 km Time spent on track = T = 60 seconds V2 = 2 A X X = ½ A T2If a sled is moving at 3 km/s then a centripetal acceleration of 5 g corresponds to a radius of curvature of 180 km. The last half of the track has to be straight.
If we launch inanimate equipment at an acceleration of 500 m/s2 then the track length is 9 km.
 |
 |
|---|---|
 |
|---|
The moon is ideal for sled launch because:
*) The lunar orbit speed is 1.68 km/s, well below the practical maximum of 3 km/s for sleds. The sled can be launched directly to orbit without needing a rocket stage.
*) The moon has no atmosphere and so you can launch horizontally and none of the kinetic energy is wasted on vertical motion.
*) Horizontal launch allows the track to be arbitrarily long, enabling human-friendly low-g launch.
*) The moon has abundant iron from metallic asteroid impacts for constructing the track.
The moon has abundant ice in polar craters and it can be launched into space in bulk with sleds. If the sled power comes from solar cells then the mass launch rate is:
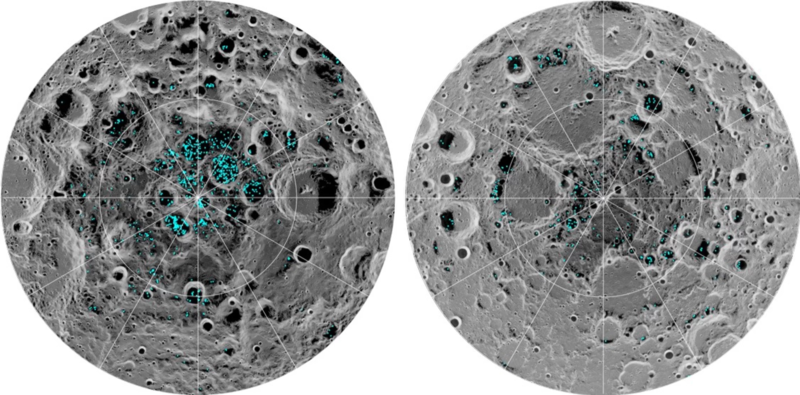
Launch speed = V = 1.68 km/s Launch energy/mass = e = ½ V2 = 1.41 MJoules/kg Solar cell average power = p = 200 Watts/meter2 Solar cell area = A meters2 Launch power = P = p A = e m Watts Mass launch rate = m = p A / e kg/secondA spaceship needs 1000 tons of ice to shield cosmic rays. Launching this much ice in one month requires .5 MegaWatts and 2500 meters2 of solar cells.
Mars is ideal for a launch sled because the orbit speed is small, the air is thin, and there is a tall mountain. Launch at near horizontal angle is possible from the mountain.
Mars launch speed = 3.6 km Sled practical max speed = 3 km/s Mars airmass = .16 tons/meter2 Earth airmass = 10.1 tons/meter2 Mars Mount Olympus height = 21.2 km Earth Mount Everest height= 8.8 km
 |
 |
|---|---|
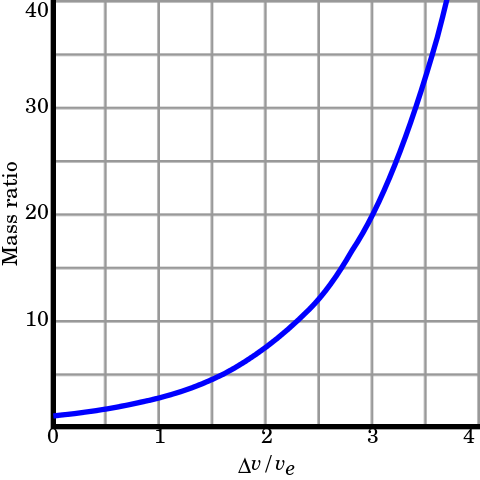
Jupiter provides the most powerful assist and is used for all missions to the outer solar system. Voyager 2 benefitted from an assist from all 4 gas giants.
 |
|---|
The Oberth maneuver uses a planet's gravity to magnify a rocket impulse. Planets act like powered pinball buffers.
Suppose a spacecraft is on a highly elliptical orbit, with a perigee slightly larger than the Earth's radius and an apogee vastly larger than the Earth's radius.
Gravity constant = G = 6.67e-11 Newton meters2/kg2 Mass of Earth = M = 5.97e24 kg Earth radius = R = 6371 km/s Perigee radius = R1 Slightly larger than R Apogee radius = R2 R1 << R2 Escape velocity = Vesc= 11.2 km/s Rocket speed at perigee = V1 = Vesc Rocket speed at apogee = 0 Circular orbit speed at perigee = Vcirc= 7.2 km/s = G M / R1 Circular orbit speed at apogee = 0 Rocket speed change at perigee = Vroc = 16.6 km/s Calculated below Final exit speed from planet = Vexit= 25.4 km/s Final speed after far from the planetAt apogee the energy is
E = Kinetic energy + Gravitational energy = 0 + 0At perigee the energy is
E = Kinetic energy + Gravitational energy
= .5 m V12 - G M m / R1
V12 = 2 G M / R1
= 2 Vcirc2
= Vesc2
V1 is equal to the "Escape speed", the speed required to escape the planet.
The escape speed is independent of the direction of the velocity.
The escape velocity can also be obtained from the gravitational potential energy.
.5 m Vesc2 = G M m / R1 → Vesc2 = 2 G M / R1If the rocket fires at perigee and increases its speed by Vroc, the energy becomes
E = .5 m (V1 + Vroc)2 - G M m / R1 = .5 m (Vesc + Vroc)2 - .5 m Vesc2 = .5 m (Vroc2 + 2 Vroc Vesc)The rocket is now on a hyperbolic orbit and will escape the Earth, As it recedes from the Earth it will approaches a constant velocity Vexit. When far from the Earth, the energy is
E = .5 m (Vroc2 + 2 Vroc Vesc) = .5 m Vexit2 Vexit= (Vroc2 + 2 Vroc Vesc)1/2 > VrocIf the spacecraft starts in an elliptical orbit and changes its speed by Vroc at perigee, it departs the Earth at speed Vexit, which is larger than Vroc. This is the "Oberth effect".
If a rocket changes its velocity by 5 km/s at perigee, it departs the Earth with a velocity of
Vexit= (52 + 2 * 5 * 11.2)1/2
= 11.7 km/s
This gets you to Mars in about 4 months.
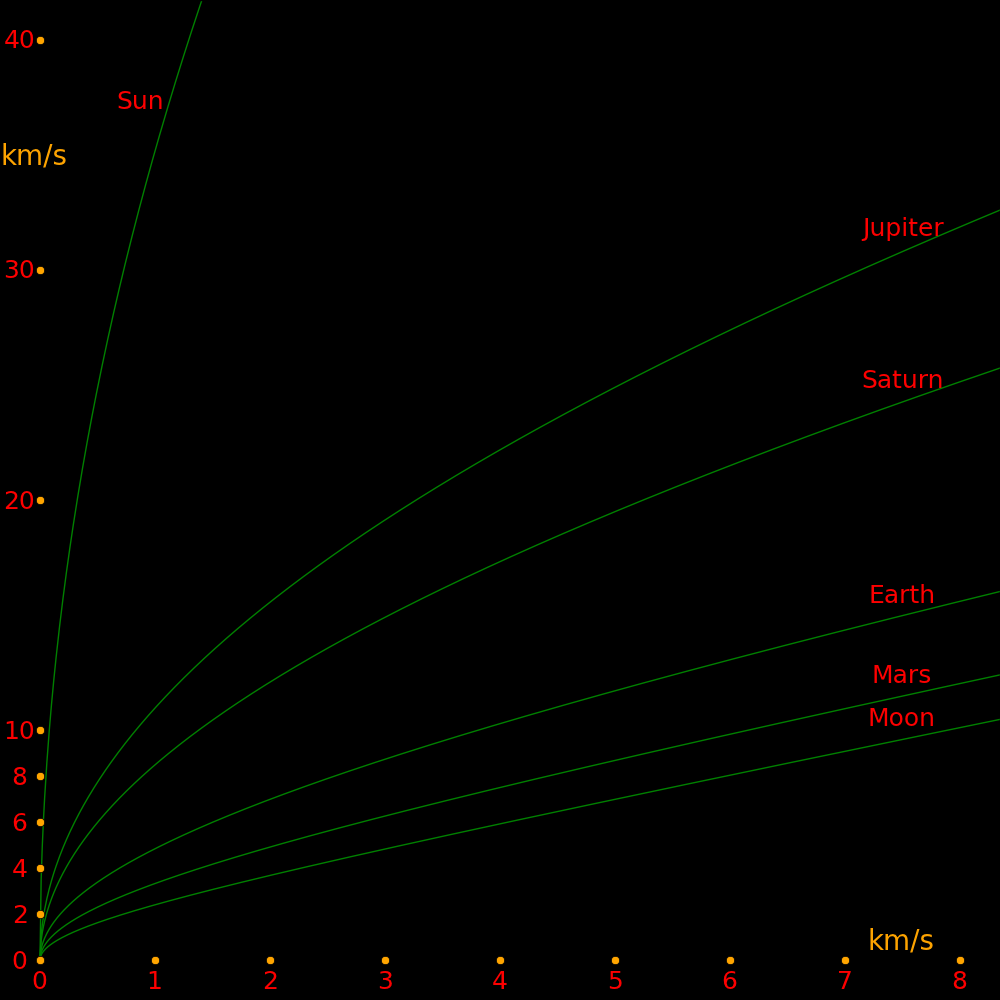 |
|---|
X axis: Change in velocity at perigee (Vroc) Y axis: Departure velocity from the planet. Vexit = (Vroc2 + 2 Vroc Vesc)
Each curve corresponds to a different planet.
Escape speed Orbit speed
km/s km/s
Moon 2.38 1.02
Earth 11.2 29.8
Mars 5.03 24.1
Jupiter 59.5 13.1
Saturn 35.5 9.64
Uranus 21.3 6.81
Neptune 23.5 5.43
Sun 618 -
The Oberth maneuver requires a rocket with a large thrust-to-mass ratio. The Oberth effect is most useful when the rocket fires at Perigee, meaning the rocket has only a limited time to burn through its fuel. This restricts the rocket types that can be used for an Oberth maneuver. Chemical rockets deliver the most power, which makes them the rocket of choice for Oberth maneuvers. Nuclear rockets have a heating challenge. Ion drives and mirror-based rockets are low-thrust and can't be used for the Oberth maneuver. The rocket engine with the largest force/mass is the Vulcain-2. For this rocket,
Planet radius = R = 6371 km for the Earth
Escape velocity = Ves= 11.2 km/s for the Earth
Oberth time = T = 9.5 minutes for the Earth = R / Ve
= Time that the rocket is near perigee
Rocket exhaust speed = Vex= 4.2 km/s
Rocket force = F = 1359 kiloNewtons
Rocket engine mass = m = 1800 kg
Rocket force/mass = Z = 755 Newtons/kg = F / m
Fuel mass burnt = M = T Z m / Vex = 102 m Fuel mass burnt during one Oberth time
Oberth velocity = Vob= 16.6 km/s = 3.9 Vex = [ln(M/m) - ln(2)] Vex = ln(.5 T Z / Vex) Vex
= [ln(T) - 2.4] Vex
Momentum conservation: M Vex = F T
During one Oberth time, a Vulcain-2 rocket burns 102 times its mass in fuel. The Oberth
time for the Earth is long enough so that a chemical rocket can comfortably burn through all its
fuel.
To calculate the Oberth velocity, we use the Tsoilkovsky rocket equation and assume that the final mass of the spaceship is twice the mass of the rocket engine.
Escape Radius Oberth Oberth Exit
(km/s) time (s) velocity velocity
(km/s) (km/s)
Mercury 4.3 .38 563 16.5 20.4
Venus 10.5 .95 576 16.6 25.0
Earth 11.2 1.00 569 16.6 25.4
Moon 2.38 .27 723 17.6 19.8
Mars 5.03 .53 671 17.3 21.7
Jupiter 59.5 10.9 1167 19.6 52.1
Saturn 35.5 9.0 1615 20.9 43.9
Uranus 21.3 3.97 1187 19.7 35.0
Neptune 23.5 3.86 1046 19.1 35.6
Pluto 1.23 .184 953 18.7 19.9
Sun 618 109.2 1126 19.4 156.2
"Exit velocity" is the maximum exit velocity from the planet using the Oberth maneuver.
It is also equal to the maximum "capture velocity" for using the Oberth maneuver to be captured
by a planet.
 |
|---|
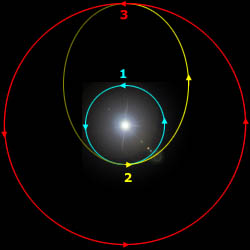
A Hohmann trajectory takes you from one circular orbit to another, such as from Earth's orbit to Mars' orbit.
The spacecraft starts on the cyan circular orbit.
At point "2", the spacecraft fires its rockets and increases its speed. From there, it coasts along the yellow trajectory to point "3".
When the spacecraft arrives at point "3", it fires its rockets to decrease its speed, placing it on the circular red trajectory.
In a trip from the Earth to Mars, the Earth is at point "2" and Mars is at point "3".
Departure velocity from the Earth = 2.95 km/s Arrival velocity with respect to Mars = 2.65 km/s Travel time from Earth to Mars = 8.5 months Wait time on Mars for Hohmann window = 14.9 months Travel time from Mars to Earth = 8.5 months Total mission time = 31.9 monthsThe total change in velocity that the rocket has to generate is 5.60 km/s. This is within the reach of a hydrogen+oxygen rocket, which has an exhaust speed of 4.4 km/s. This is the minimalist trajectory. If more rocket power is available then the travel time decreases.
Calculation of the Earth-Mars Hohmann orbit
 |
 |
 |
|---|---|---|
Using Lagrange points and gravity assists, objects can be moved around the solar system with minimal propulsion. With minimalist nudges you can set up billiards-style trick shots and move large objects wherever you like. This is the "interplanetary transport network".
 |
 |
 |
 |
|---|---|---|---|
Astronauts can expect luxuriously large spaceships. The Bigelow BA-330 has as much room as the bridge of the Enterprise and the Bigelow Genesis has as much room as a Humvee. Bigelow habitats are lighter than NASA habitats and have thicker walls. Thicker walls are helpful for defending against micrometeorites and radiation.
Mass (tons) Volume (m3)
Bigelow BA-330 23 330
Bigelow Genesis 3 11
 |
 |
|---|---|
The space station life support system requires:
Power = 1 kWatt/person Water = 1 kg/person/day Food = 1 kg/person/day
 |
 |
 |
 |
|---|---|---|---|
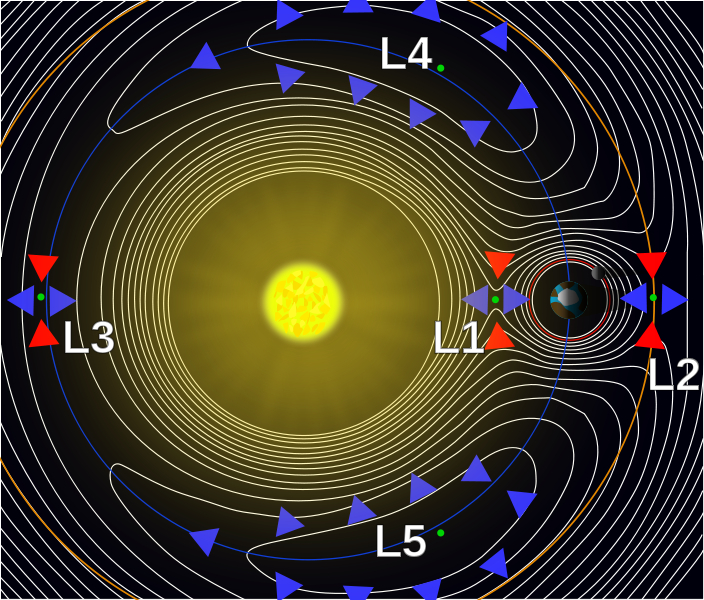
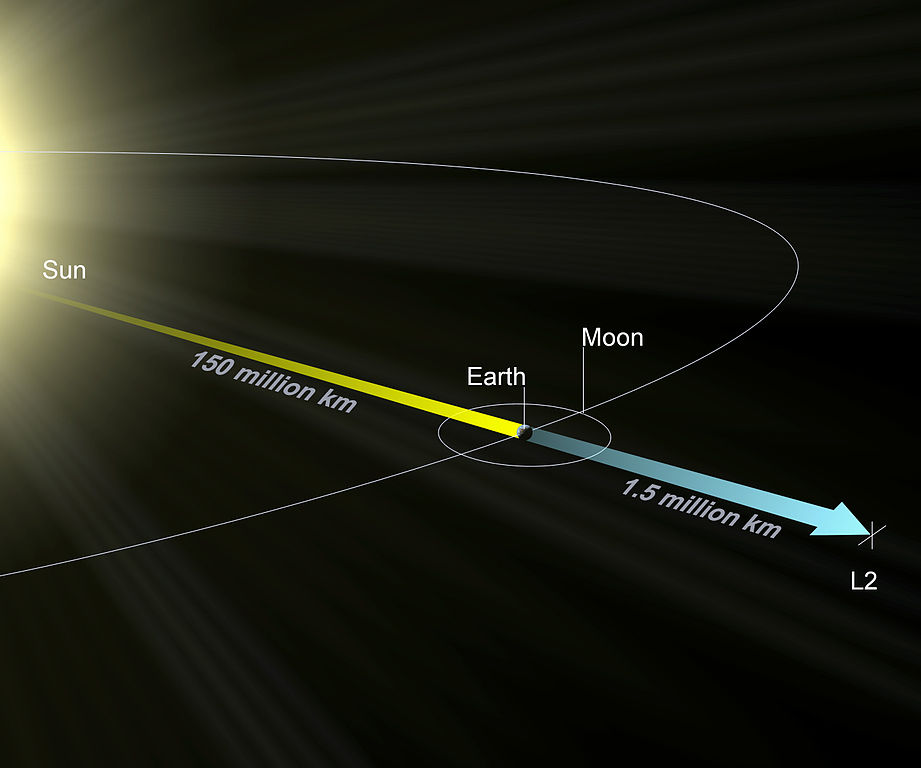
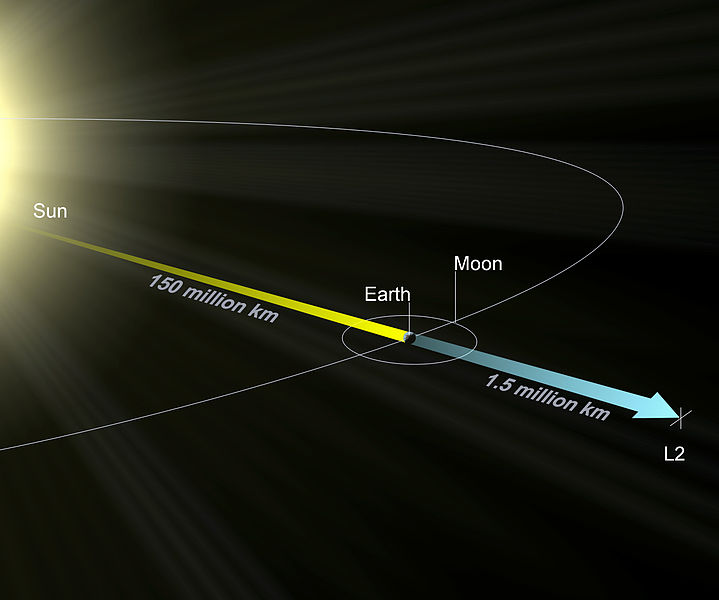
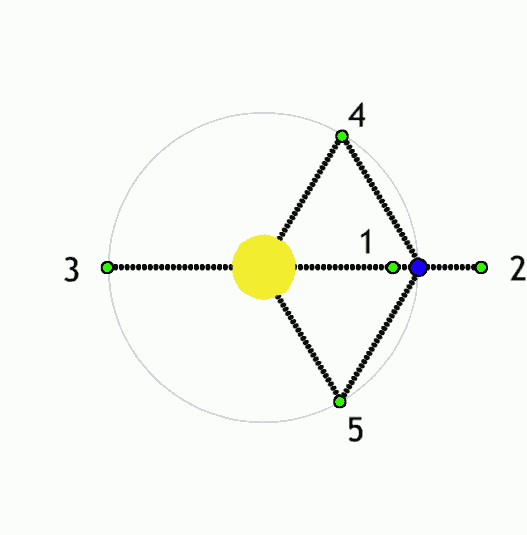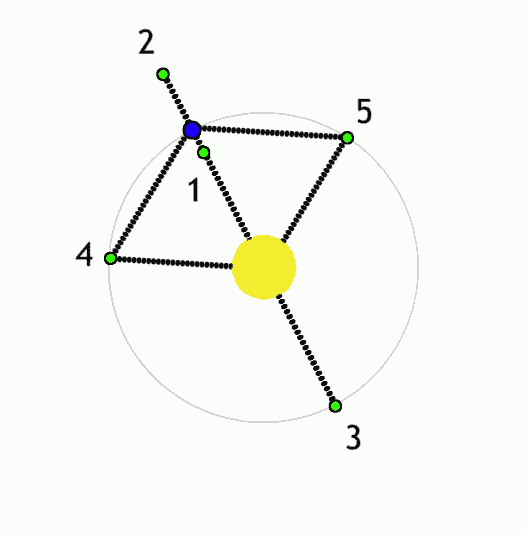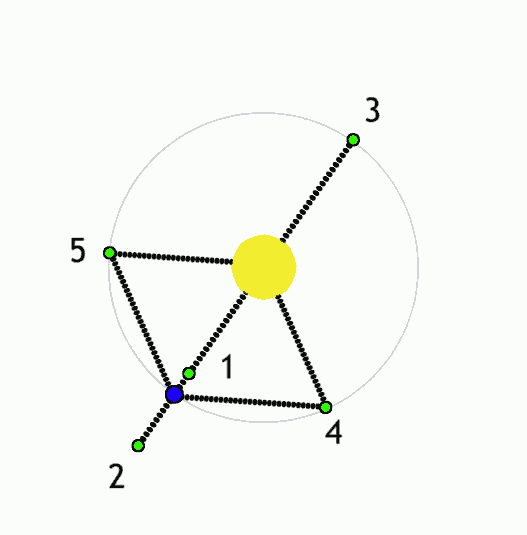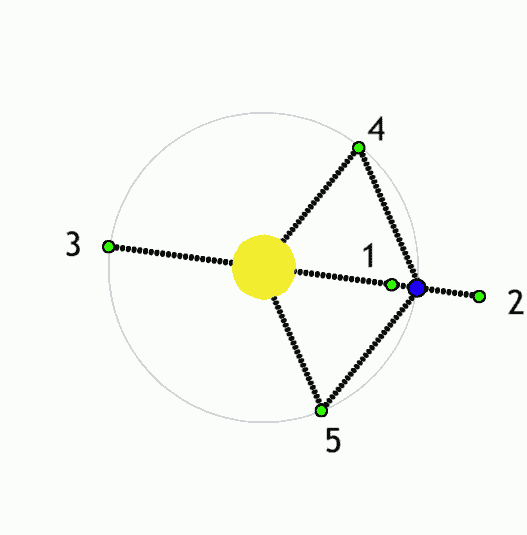
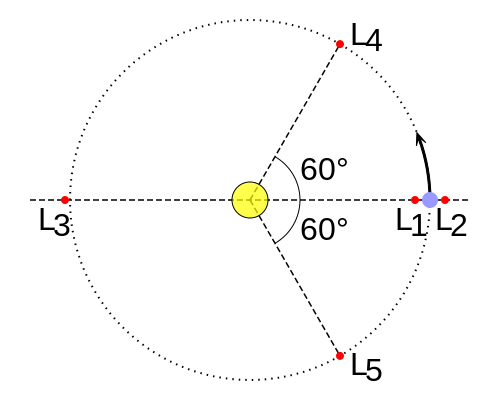
The Lagrange L2 point orbits the sun synchronously with the Earth. It's the best place for space telescopes because it's possible there to simultaneously block out light from the sun, moon, and Earth. The Webb telescope will be sent to L2 when completed.
Existing space telescopes suffer disadvantages because they're not manned. They have to function automously, they have to be prebuilt on the Earth, and they have to be sturdy enough to survive the launch into space.
If you have a manned space station these problems don't exist. Telescopes can be built on site from prefabricated modules. For example, small mirror segments can built on Earth, launched into space, and assembled to form a large mirror. Assembling mirror segments is easy in space because of the zero gravity. A manned space station also makes it possible to operate and repair the telescope on site.
The largest space telescopes are:
Diameter Wavelength Location Mass
meters tons
Spektr-R 10 Radio Geocentric 2.5
Planck 1.9 Millimeter L2 .21
Webb 6.5 Infrared L2 6.5
Hubble 2.4 Visible Low Earth orbit 11.1
Chandra 1.2 X-ray Geocentric 4.8
Fermi 1.8 Gamma ray L2 4.3
The only limit to the size of a space telescope is the amount of mass that can be
launched from the Earth. Launching 1000 tons into space costs 2 billion
dollars. We can expect that the new generation of space telescopes will have masses
on the order of 1000 tons and diameters on the order of 100 meters.
 |
 |
 |
|---|---|---|
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|
 |
 |
 |
|
|---|---|---|---|
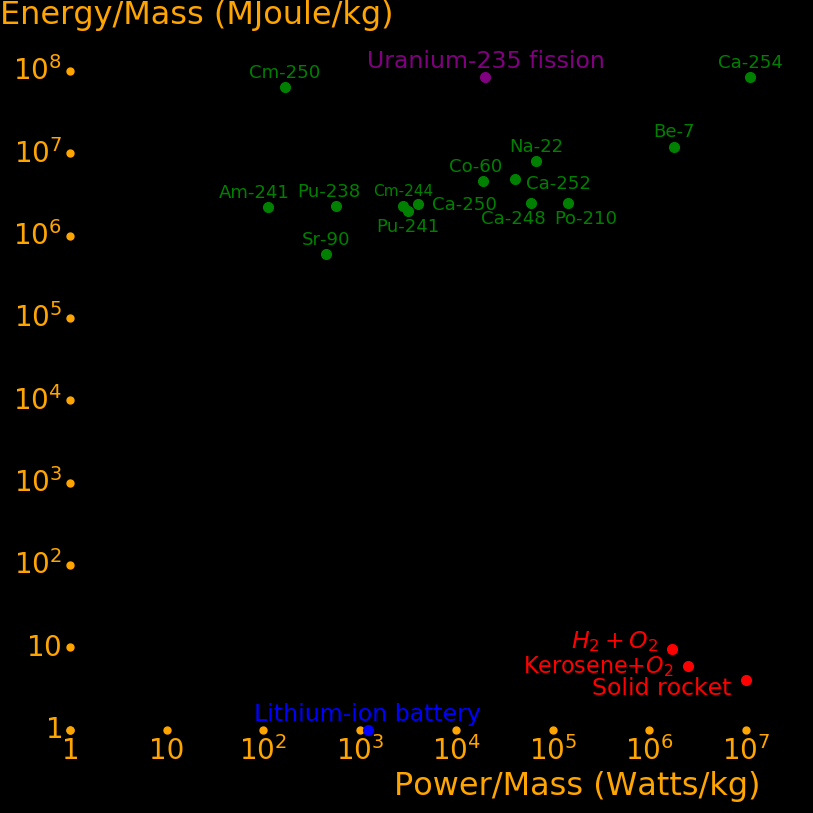
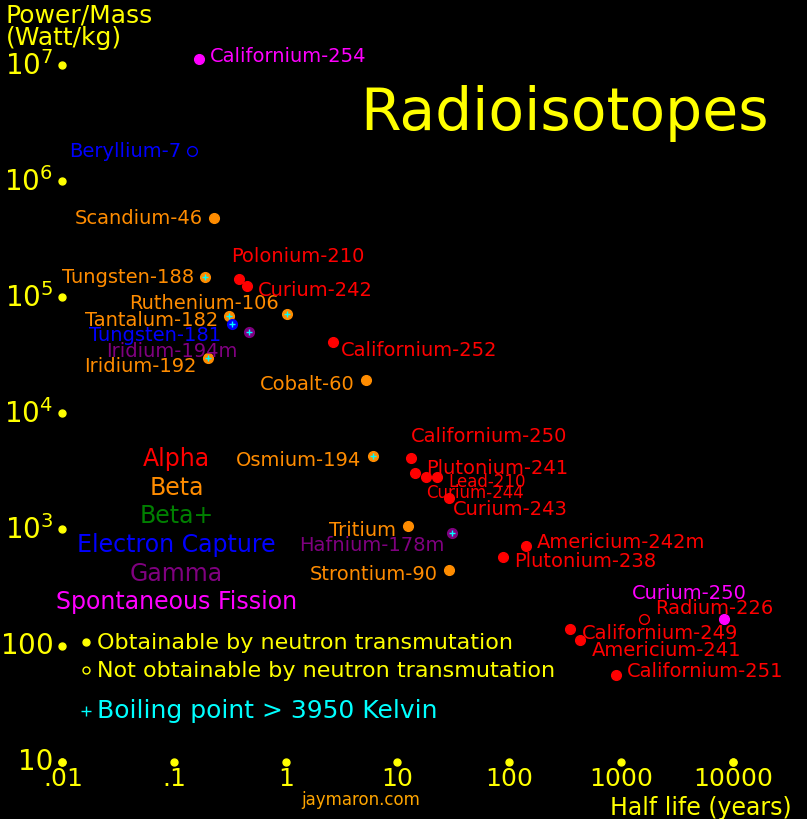
Radioisotopes have more energy per mass than gasoline by a factor of 1 million. They can power an aircraft for 50 years and they power the Voyager spacecraft. They can make a fission bomb the size of a softball. Iron Man gadgets are possible with them. Important isotopes include:
Half life (year) Use
Tritium 12.3 Fusion fuel
Helium-3 Stable Fusion fuel. Dilution refrigerator. Fission afterburner rocket
Uranium-235 704000000 Fission fuel. Fission bomb
Plutonium-239 14100 Fission fuel. Fission bomb
Thulium-170 .352 Power
Polonium-210 .379 Power. Alpha rocket
Thorium-228 1.91 Power. Alpha rocket
Thulium-171 1.91 Power. Safe around humans because it requires low radiation shielding
Caesium-134 2.06 Power
Cobalt-60 5.27 Power
Europium-152 13.5 Power
Strontium-90 28.9 Power
Uranium-232 68.9 Power. Alpha rocket
Plutonium-238 87.7 Power. Alpha rocket
Radium-226 1599 Power. Breeder for Thorium-228 and Uranium-232
Lithium-6 Stable Fission afterburner rocket. Fusion bomb
Boron-10 Stable Fission afterburner rocket. Cancer treatment
Beryllium-7 .146 Fission afterburner rocket
Sodium-22 2.602 Fission afterburner rocket
Americium-242m 141 Fission afterburner rocket
Californium-251 900 Fission afterburner rocket. Compact fission bomb. Large neutrons/fission
Californium-252 2.65 Spontaneous fission. Compact fission bomb. Large neutrons/fission
Curium-250 8300 Spontaneous fission
Carbon-12 Stable Isotopically-pure diamonds, nanotubes, and graphene
Carbon-14 5700 Low neutron capture cross section
Iridium-192 .202 Power at high temperature
Tantalum-182 .313 Power at high temperature
Tungsten-181 .332 Power at high temperature
Osmium-194 6.02 Power at high temperature
 |
 |
|---|---|
Isotope radioactivity can make electricity. The Voyager spacecraft are powered by plutonium-238.
 |
|---|
The isotopes with high power/mass are:
Half life Heat Decay Decay Obtainable by
year Watt/kg MeV neutron transmutation
Californium-254 .166 11200000 Fission 207 *
Iridium-192 .202 29942 β 1.460 *
Scandium-46 .229 485000 β 2.366 *
Thulium-170 .352 33150 β .968 *
Thulium-171 1.91 606 β .0965 *
Caesium-134 2.06 15300 β 2.059 *
Californium-252 2.64 41400 α or Fission 12.33 * α 96.9% (6.12 Mev). Fission 3.09% (207 MeV)
Cobalt-60 5.27 19300 β 2.824 *
Europium-154 8.59 3030 β 1.968 *
Tritium 12.33 315 β .0186 *
Europium-152 13.5 1821 β & EC 1.86 *
Strontium-90 28.9 2234 β, &beta 2.826 *
Caesium-137 30.1 583 β 1.176 *
Plutonium-238 87.7 578 α 5.59 *
Americium-242m 141 725 2α 12.33 *
Silicon-32 153 1159 β, β 1.92 *
Iridium-192m 241 72 IT, β 1.615 *
Curium-250 8300 170 Fission 148 * Fission 74%, Alpha 18%, Beta 8%
Beryllium-7 .146 1822000 EC .547
Hafnium-172 1.87 11700 EC 1.835
Hafnium-172 1.87 11700 EC 1.835
Sodium-22 2.6 68700 β+ or EC 2.842
Rhodium-101 4.07 9890 EC 1.980
Titanium-44 59.1 4318 EC, β+ 3.798
Thorium-227 .0512 9194000 5α+2β 36.14
Uranium-230 .0554 9280000 6α+2β
Thorium-228 1.912 235000 5α+2β 34.784
Radium-228 5.75 90660 5α+4β 40.198
Actinium-227 21.8 21600 5α+3β 36.18
Uranium-232 68.9 7545 6α+2β 40.79
Radium-226 1599 286 5α+4β 34.958
Thorium-229 7917 57.7 5α+3β 35.366
Protactinium-231 32600 16.2 6α+3β 41.33
Thorium-230 75380 6.78 6α+4β 39.728
 |
|---|
A battery that's around humans needs radiation shielding. Gammas are the most penetrating radiation, so what matters is the highest-energy gamma produced. Alpha and beta decay produce gammas by bremsstrahlung, and a charged particle can give all its energy to one gamma.
The isotopes with low-energy gammas are:
Half life Power/mass Decay Gamma Stopping Formation Obtainable by Decay
energy max length rate neutron
year Watt/kg MeV MeV mm barn*year transmutation
Nickel-63 100.1 5.52 .017 .017 .004 2.5 * β
Tritium 12.33 315 .0186 .0186 .005 71 * β
Rubidium-83 .236 .910 .0322 0 EC
Samarium-145 .931 .617 .061 .022 * EC
Tantalum-179 1.82 .110 .065 0 EC
Promethium-145 17.7 131 .164 .072 .022 * EC
Platinum-193 50 17.5 .057 .076 3.81 * EC
Thulium-171 1.91 606 .096 .096 .09 30.8 * β
Europium-155 4.76 705 .252 .147 312 * β
"Gamma" is the energy of the highest-energy gamma produced.
"Stopping length" is the stopping length of the gamma in iridium. The radiation shield should be at least 10 times thicker than the stopping length.
"Formation rate" indicates of how fast it can be produced in a nuclear reactor. See the "Hurdle" section below.
 |
 |
 |
 |
|---|---|---|---|
Isotopes exist with a critical mass smaller than plutonium-239. The smallest critical mass is californium-252 at 2.7 kg. The critical sphere diameter is 6.9 cm, the size of a tennis ball.
Half life Critical Critical Density Fission
mass diameter barn
year kg cm gram/cm3
Californium-252 2.64 2.73 6.9 15.1 33
Californium-251 900 5.46 8.5 15.1 4894
Californium-249 351 6 9 15.1 1666
Curium-247 15700000 7 9.9 13.5 82
Plutonium-239 14100 10 9.9 19.8 748
Uranium-233 159000 15 11 19.1 536
Uranium-235 704000000 52 17 19.1 538
Natural uranium has a critical mass of 800 with heavy water moderator, and 10000 kg with graphite moderator.
 |
|---|
An isotope that sponteously fissions is a neutron source. The easiest such isotope to make is californium-252. The isotopes with a large spontaneous fission rate are:
Fission Decay Neutrons Fission
half life Half life per fraction
years years fission
Mendelevium-260 .0895 .0761 .85
Californium-254 .166 .166 .997
Californium-252 85.7 2.65 3.73 .0309
Curium-250 11200 8300 3.31 .74
 |
|---|
A fission thermal rocket uses a fission reactor to heat hydrogen exhaust. The higher the temperature, the faster the exhaust. The temperature limit is of the order 4000 Kelvin because this is the highest temperature for which solids exist. The material with the highest melting point is hafnium carbide at 4201 Kelvin.
A fission reactor can alternately heat exhaust by generating neutrons, which trigger fission in the exhaust. The neutrons are generated as a pulse and the exhaust is pulsed. The likelihood for a neutron to trigger fission is quantified as a "cross section". The isotopes with the largest fission cross section are:
Half life Fission Energy Quality Neutron capture Obtainable by
year barn MeV output neutron transmutation
Americium-242m 141 7024 195 5640 Daughter nuclei + Neutrons *
Californium-251 900 4894 207 3940 Daughter nuclei + Neutrons *
Curium-245 8500 2161 198 1740 Daughter nuclei + Neutrons *
Plutonium-239 14100 748 189 590 Daughter nuclei + Neutrons *
Uranium-235 704000000 538 181 410 Daughter nuclei + Neutrons *
Beryllium-7 .146 56800 1.644 11670 Lithium-7 + Proton
Sodium-22 2.602 27490 4.14 4948 Neon-22 + Proton
Helium-3 Stable 5333 .764 1020 Tritium + Proton *
Boron-10 Stable 3835 2.34 820 Lithium-7 + Alpha *
Lithium-6 Stable 940 4.783 640 Alpha + Tritium *
Zirconium-88 .228 861000 8 77000 Zirconium-89 + Gammas
Gadolinium-157 Stable 259000 7.94 13020 Gadolinium-158 + Gammas *
Gadolinium Stable 49000 8 2500 Gadolinium-158 + Gammas * Natural composition
An isotope's quality as fission afterburner fuel is
Atomic mass number = M Dimensionless Fission energy = E MeV Fission cross section = A barns Afterburn quality = Q = AE/M
Many superisotopes are actinides. The orange line shows the isotopes can be produced by neutron capture.
 |
|---|
Neutron capture transmutes an isotope one space to the right and beta decay transmutes an isotope one space up. Isotopes on or to the right of orange lines can be made with neutron transmutation and isotopes to the left of the lines can't. Elements that are made by neutron-transmutation tend to be neutron-heavy (neutronic), and elements that can't be made by neutron-transmutation tend to be proton-heavy (protonic).
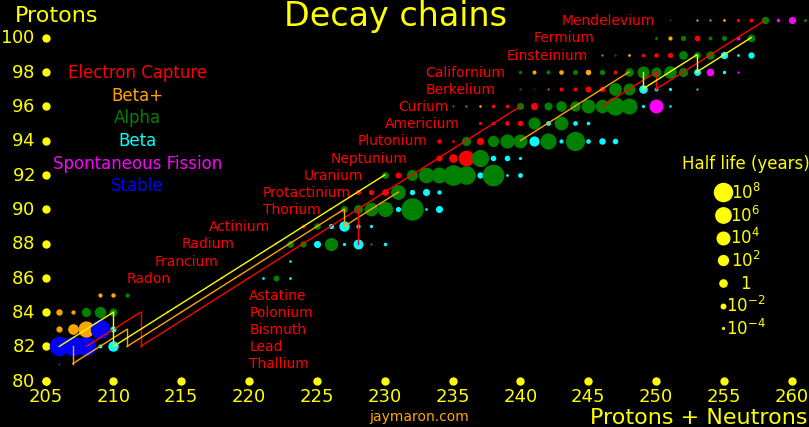 |
|---|
Suburanics are the isotopes from radium to uranium. Many undergo 5 or 6 alpha decays, such as uranium-232. This is the red line in the plot.
 |
|---|
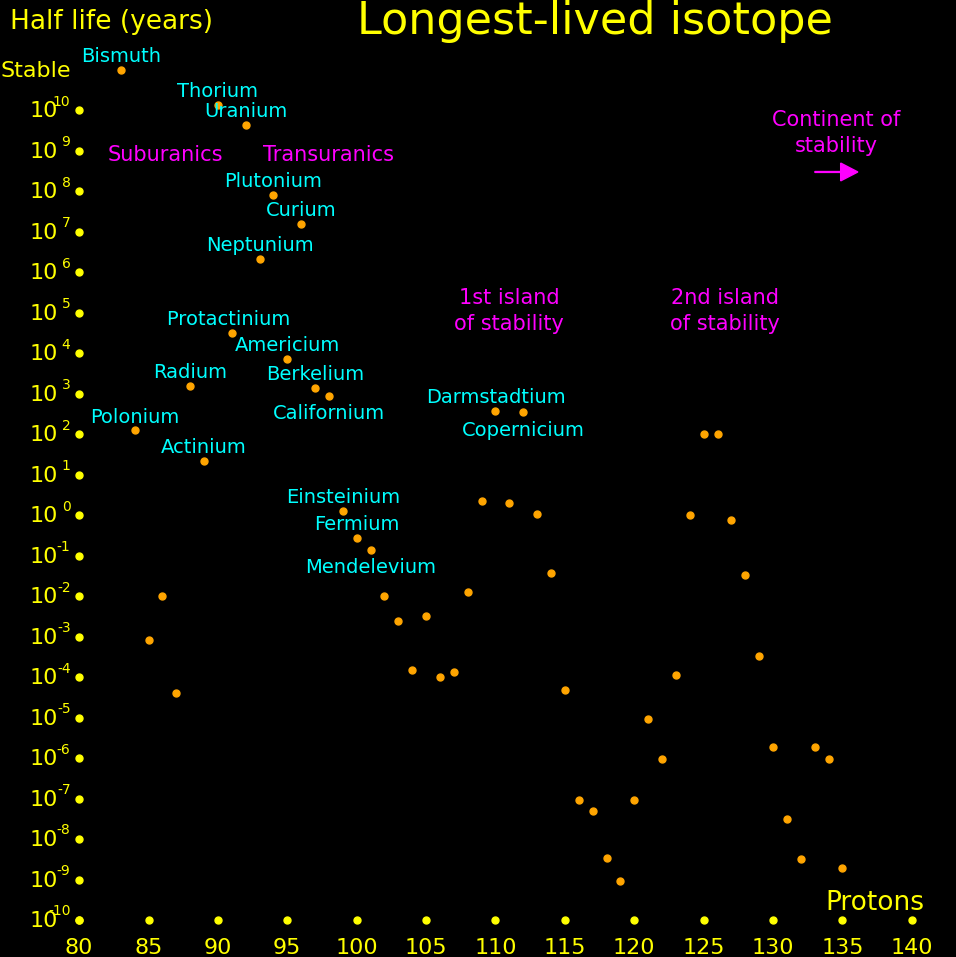
There is a hypothetical "island of stability" around atomic number 112 where isotopes may be long-lived. A second island may exist at atomic number 126.
Experiments can only measure the longest-lived isotope up to a proton number of 105, and beyond that we plot theory. Theoretical half lives are uncertain by an order of magnitude.
 |
|---|
It's possible that for large nucleon number, larger than around 300, that the nucleus transitions to a lower-energy state, called "Up down quark matter", or "udQM". The existence of udQM is unresolved. Theory is uncertain, and it hasn't been experimentally produced. The largest nucleus that's been produced is oganesson-294, with 118 protons and 294 nucleons. It shows no sign of udQM, so if udQM exists, it's beyond oganesson.
If udQM nuclei exist, they could potentially be long-lived. They don't fission because it would take the nucleus to a higher-energy state. They decay by alpha until they're too light to be udQM, at which point they fission.
If udQM nuclei exist, then there may exist long-lived elements from Z=140 to way beyond. These are "continental elements".
The largest nucleus that standard nuclear matter can make has Z=140. Larger nuclei fission instantly. The only way that nuclei with Z>140 can exist is if udQM exists.
Typical energies:
MeV MeV/Nucleon
Chemical reaction .000002 Varies
Beta decay 2 Varies
Alpha decay 6 .026
Superalpha decay 36 .16 5 or 6 alphas, in sequence. For example, Uranium-232
Superheavy decay 280 .98 Alpha, then fission. Superheavy elements with more than 108 protons
Neutron capture 8 Varies
Fission (Helium-3) .764 .19
Fission (Lithium-6) 4.783 .68
Fission (Beryllium-7) 1.64 .21
Fission (Boron-10) 2.34 .21
Fission (Uranium-235) 181 .77
Fission (Plutonium-239) 189 .79
Fission (Californium-252) 207 .82
Fusion of D+Li6 22.4 2.8
Beta decay, Beryllium-7 .547 .078
Beta decay, Sodium-22 2.842 .13
Beta decay, Scandium-46 2.366 .051
Beta decay, Cobalt-60 2.82 .047
 |
|---|
Half life Heat Decay Decay energy Melt Boil Obtainable by Formation rate
year Watt/kg MeV Kelvin Kelvin neutron transmutation
Tungsten-188 .191 148700 2β .349 3695 6203 * .173
Iridium-192 .202 * 193
Tantalum-182 .313 68866 β 1.814 3290 5731 * 6.42
Tungsten-181 .332 59200 EC 1.732 3695 6203 * .0239
Ruthenium-106 1.023 71200 2β 3.584 2607 4423 * .000198
Hafnium-172 1.87 11700 EC 1.835 2506 4876
Thorium-228 1.912 235000 5α+2β 34.784 2023 5061
Rhodium-101 4.07 9890 EC 1.980 2237 3968
Cobalt-60 5.27 19300 β 2.82 1768 3200 * 2.01
Osmium-194 6.02 4313 2β 2.33 3306 5285 * .130
Platinum-193 50 17.5 EC .057 2041 4098 * 3.81
Titanium-44 59.1 4318 EC & β+ 3.798 1941 3560
Uranium-232 68.9 7545 6α 40.79 1405 4404
Iridium-192m2 241 72 * 100
Thorium-229 7917 57.7 5α+3β 35.366 2023 5061
Protactinium-231 32600 16.2 6α+3β 41.33 1841 4300
Europium-152 13.5 8660
Europium-154 8.59 312
Europium-155 4.76 312
Meitnerium-285 2.24 1020000 α+fission 220 ~3300 ~5000
Darmstadtium-293 37.7 58900 β+fission 220 ~2600 ~4700
Darmstadtium-292 133 16700 α+fission 220 ~2600 ~4700
Darmstadtium-294 380 5820 α+fission 220 ~2600 ~4700
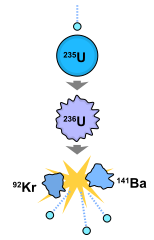 |
|---|
Half life Fission Fission Critical mass
year barn neutrons kg
Fermium-257 .275 2100 5.7
Einsteinium-254 .75 2900 4.2 9.9
Californium-251 900 4801 4.1 5.46
Californium-249 351 600 4.06 6.0
Curium-245 8500 2161 3.83 9.6
Americium-242m 141 7024 3.26 9.5
Plutonium-239 14100 748 2.89 10
Uranium-235 704000000 538 2.43 52
The transmutation options are:
Example Means
Add a neutron Uranium-238 → Uranium-239 Slow neutrons from fission. Thermal neutrons at 300 Kelvin and .025 eV
Subtract a neutron Thorium-232 → Thorium-231 Superfast neutrons from fusion. Neutron energy = 14.1 MeV
Beta decay Uranium-239 → Plutonium-239 Patience
Alpha decay Uranium-233 → Thorium-229 Patience
Fission Uranium-235 → Daughter nuclei + Neutrons
Accelerator substitution Lithium-6 + Deuteron → Beryllium-7 + Neutron
Accelerator fusion Berkellium-249 + Calcium-48 -> Tennessine-297
Some isotopes can be made with present technology and some need future technology. Also, the more energy you have, the more isotopes you can make.
Fission reactors are the easiest way to make isotopes. They produce slow neutrons that are captured by a target nucleus and they make isotopes that are "neutron heavy", or "neutronic".
Slow neutrons tend to stick to nuclei and superfast neutrons tend to eject neutrons from nuclei. Superfast neutrons can make protonic isotopes. Superfast neutrons are produced by fusion:
Deuterium + Tritium → Helium-4 (3.5 MeV) + Neutron (14.1 MeV)
Most isotopes can be made with slow or superfast neutrons. Many that can't can be made with accelerator substitution. A target nucleus is bombarded with high-energy particles such as deuterons, tritons, alphas, and He-3. For example,
Lithium-6 + Deuteron + 2 MeV → Beryllium-7 + Neutron
Isotopes can be made by fission, for example rhodium-103 and palladium-106. Rhodium and palladium are valuable catalysts.
Isotopes can be made by spallation, where a high-energy particle blasts nucleons off a nucleus.
Isotopes can be made by fusion, where 2 nuclei are collided at the resonance energy for fusion. This is how isotopes far beyond uranium are made.
Isotopes can be made by alpha decay. For example, slow neutrons turn thorium-232 into uranium-233, and then uranium-233 alpha decays to suburanics.
Slow neutrons tend to stick to nuclei and superfast neutrons tend to eject neutrons from nuclei. Superfast neutrons can make protonic isotopes. Superfast neutrons are produced by fusion:
Deuterium + Tritium → Helium-4 (3.5 MeV) + Neutron (14.1 MeV)
The cross sections for a fusion neutron hitting thorium-232 are (in barns):
Fusion neutrons Fission neutrons Thermal neutrons Energy threshold
14.1 MeV 2.4 MeV average .025 eV average MeV
Capture the neutron .0011 .096 7.299 0
Eject 1 neutron 1.786 .017 0 6.468
Eject 2 neutrons .522 .000072 0 11.61
Eject 3 neutrons 0 0 0 18.43
Fission .361 .080 .000054 0
Elastic collision 2.740 4.832 14.72 0
Inelastic collision .468 2.690 0 .0496
Total 5.859 7.717 22.02
For fusion neutrons, ejection is half the cross section.
Protonic isotopes can be produced by bombarding a target nucleus with a high-energy particle, such as a proton, deuteron, triton, He-3, or Alpha.
Beryllium-7 can't be made with fission or fusion neutrons, but it can be made by bombarding Lithium-6 with high-energy deuterons.
Target New High-energy Energy Cross section nucleus nucleus particle MeV barn Li6 Be7 d 2 .2 Mg24 Na22 d 7 .2 Th232 Ac227 t 75 .5 Th232 Ra228 t 100 .0018 Th232 Th228 d 83 .272 Th232 U-232 Alpha 38 .195 Th232 Ac225 p 150 .015 Th232 Ac226 p 150 .015 Th232 Ac227 p 150 .015 Th232 Th227 p 70 .040 Th232 Th228 p 60 .085
Suburanics can be made with a combination neutron addition and subtraction. Starting with thorium-232,
Th-232 → Th-231 → Th-230 → Th-229 → Th228
Th-232 → Th-233 → U-233 → U-232 → U-231 → U-230
Radium can be made by waiting for a thorium alpha decay.
Input Input half life Output Output half life
year
Thorium-230 75380 Radium-226 1599
Thorium-232 14000000000 Radium-228 5.75
Uranium-235 704000000 Protactinium-231 32600
Uranium-238 4470000000 Thorium-230 75380
Radium-226 can generate all the important suburanics with fission neutrons except for Uranium-230. The sequence is:
Radium-226 → Actinium-227 → Thorium-227 → Thorium-228 → Thorium-229 → Thorium-230 → Protactinium-231 → Uranium-232
Neutron capture is slow. Some isotopes need a high neutron flux. A prime goal is maximizing neutron density, and a future civilizations will have neutron densities than today.
The neutron capture rate is:
Neutron density = D = e16 neutrons/meter3 Typical for a fission reactor Neutron speed = V = 2190 meter/second Thermal neutron at 300 Kelvin Neutron flux = F = D V =2.2e19 neutrons/meter2/second Typical for a fission reactor Neutron capture cross section = A = e-28 meter2 = 1 barn Typical cross section Transmutation time = T = (DVA)-1 = 4.6e8 seconds = 14 years
Many isotopes need a small transmutation time. This can be done by increasing the neutron flux or by increasing the capture cross section. The slower the neutron, the larger the cross section.
For neutrons below 100 eV, it's often the case that "VA" is constant as a function of V.
At Oak Ridge National Laboratory, the High Flux Isotope Reactor has a flux of 2.5e19 neutrons/meter2/second.
The Oak Ridge Spallation Source produces neutron pulses with e21 neutrons/meter2/second.
Neutrons are made by hitting beryllium-9 with high-energy alphas. The alpha source is often polonium-210.
Beryllium-9 + &alpha → Carbon-12 + Neutron
Continuous flux Pulse flux Continuous power
Neutron/meter2/s Neutron/meter2/s MWatt
Supernova - e36 e30 neutrons/meter3
Fission bomb e28
Oak Ridge fission reactor 2.5e19 - 75
Oak Ridge spallation source 3e18 2e21 1.4
ITER fusion reactor 2e18 - 500
Stellar S process e15
Californium-252 e13
Polonium-210 + Beryllium-9 e12 - Polonium-210 half life = .379 years
Fusor e9 - Use high voltage to fuse D+T
Radium-226 + Beryllium-9 e8 - Radium-226 half life = 1599 years
Earth surface .0065
Deep underground e-9
In many cases, the slower the neutron, the higher the capture cross section.
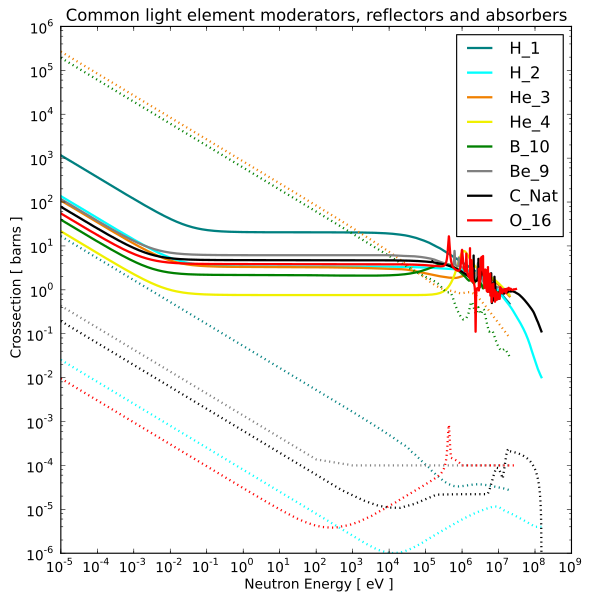 |
|---|
Solid lines are scattering cross sections and dotted lines are capture cross sections.
Kelvin
Water melt 273
CO2 sublime 195
Argon boil 87
Nitrogen boil 77
Neon boil 27
Hydrogen boil 21
Helium-4 boil 4.2
Helium-3 boil 3.2
Helium-3 evaporative cooling .3
Dilution refrigerator .002 Uses helium-3 and helium-4
Nuclear demagnetization, typical .000001
Laser cooling, typical .000001
Nuclear demagnetization, record low .0000000001
Laser cooling, record low .000000000038
Cold neutrons bounce off walls. The critical temperature for various materials is:
Neutron Neutron Neutron
temperature temperature speed
neV Kelvin meter/second
Nickel-58 335 .0039 8.14
Diamond 304 .0036 7.65
BeO 261 .0031 6.99
Nickel 252 .0030 6.84
Beryllium 252 .0030 6.84
Graphite 180 .0021 5.47
This is within reach of a dilution refrigerator, which can reach .002 Kelvin. It's also within reach of magnetic trapping.
An advanced civilization will have unlimited helium-3 and can make a large dilution refrigerator. It can make a neutron wall trap that can collect all the outgoing neutrons from a fission reactor and funnel them to a focus. The only limit on neutron density is neutron degeneracy, which is 1022 neutrons/meter3 at .003 Kelvin.
Ultracold neutrons can be trapped magnetically. Neutrons have a magnetic moment of 50 neV/Tesla. For a 3 Tesla field, this is the same temperature range as a dilution refrigerator and as for wall trapping.
Magnetic fied (Tesla)
Neodymium magnet 1.25
Magnetic resonance imaging 7
Superconducting magnet max, continuous operation 32
Resistive magnet max, continuous operation 38
Pulsed magnet max, non-destructive 100
Pulsed magnet max, destructive 2000
White dwarf 1000
Neutron star 10000000
Magnetar 10000000000
Magnetar max 100000000000
Neutron density is limited by degenercy pressure. For neutrons,
Type Energy Temperature Wavelength Speed Degenerate density
eV Kelvin Angstroms Meter/second #/meter3
Fusion 14100000 .000061 51900000
Fast 2000000 .00016 19600000
Thermal .0253 294 1.45 2200 3.3⋅1029
Cold .00036 4.2 12.1 263 5.6⋅1026
Ultracold .00000022 .0025 497 6.4 8.1⋅1021
Fast neutrons are from fission.
Fusion neutrons are from the fusion of D+T->He4+n, which produces a 14.1 MeV neutron.
 |
|---|
Half life Neutron capture (barns)
Osmium-192 Stable 3.12 Input isotope
Osmium-193 1.25 days 38.0 Hurdle isotope
Osmium-194 6.0 years .043 Output isotope
If there is a hurdle isotope, the formation rate of the output isotope is proportional to:
Hurdle half life = T Hurdle neutron capture cross section = σc Hurdle fission cross section = σf Natural fraction = F Fraction of the natural element that can transform to the output isotope Capture fraction = C = σc/(σc+σf) Formation rate of output isotope = Q = T σc F C
This is for the case of an output isotope with a long half life and a hurdle isotope with a short half life.
If the output isotope has a short half life, then the output isotope is the hurdle. "T" becomes the half life of the output isotope and σc becomes the capture cross section for the isotope preceeding the output isotope.
If the hurdle time is more than 1 year, we use a time of 1 year.
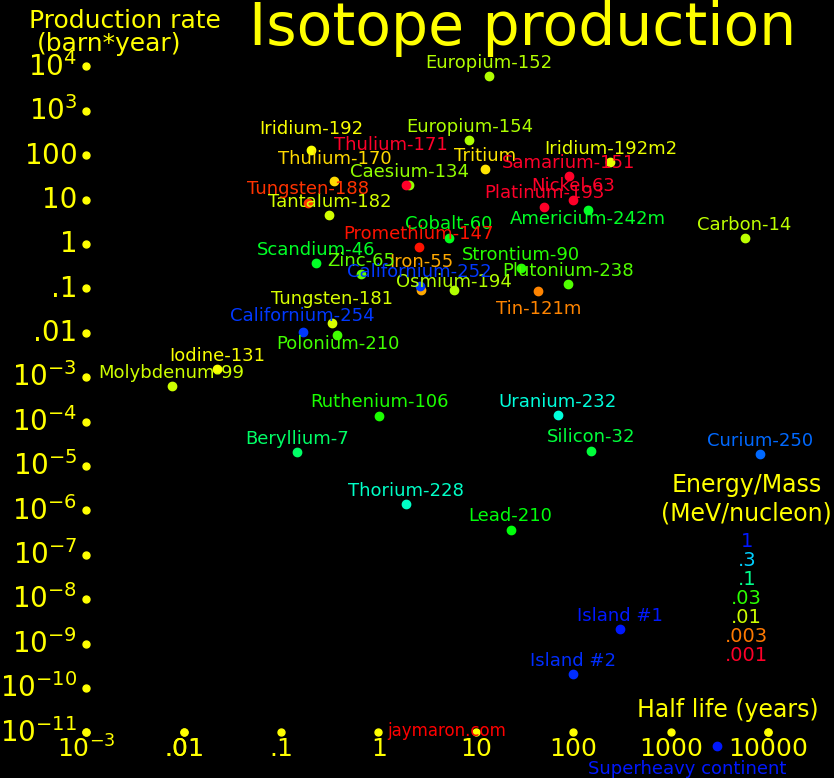 |
|---|
In the plot, "Island #1 and #2" are the nuclear islands of stability. Island #1 needs a formation time of order .1 seconds, and island #2 needs .01 seconds, and superheavy isotopes (udQM regime) need .001 seconds.
The isotopes with hurdles to their formation are:
Output Output Hurdle Capture Natural Capture Production Hurdle
Half life half life rate
year year barn fraction fraction barn*year
Europium-152 13.5 13.5 9100 .952 1 8660 Europium-151
Europium-154 8.59 8.59 312 1 1 312 Europium-153
Europium-155 4.76 4.76 312 1 1 312 Europium-153
Iridium-192 .202 .202 954 1 1 193 Iridium-192
Iridium-192m2 241 241 100 1 1 100 Iridium-192m2
Tritium 12.3 Stable 940 .0759 1 71 Lithium-6
Thulium-170 .352 .352 105.6 1 1 37.2 Thulium-170
Thulium-171 1.91 .352 87.6 1 1 30.8 Thulium-170
Caesium-134 2.06 2.06 30.3 1 1 30.3 Caesium-137
Americium-242m 141 141 84 1 .10 8.4 Americium-242m
Tantalum-182 .313 .313 20.5 1 1 6.42 Tantalum-182
Platinum-193 50 Stable 10.0 .381 1 3.81 Platinum-192
Cobalt-60 5.27 5.27 2.007 1 1 2.007 Cobalt-60
Carbon-14 5730 Stable 1.931 .996 1 1.92 Nitrogen-14
Plutonium-238 87.7 2144000 171 .0072 .146 1.23 Neptunium-237
Argon-39 269 Stable .8 1 1 .8 Argon-38
Cadmium-109 1.26 Stable 1.1 .518 1 .57 Cadmium-108
Scandium-46 .229 .229 2.366 1 1 .542 Scandium-46
Iron-55 2.737 2.737 2.25 .0585 1 .36 Iron-55
Deuterium Stable Stable .333 .99985 1 .333 Proton
Zinc-65 .667 .667 .93 .492 1 .305 Zinc-65
Tungsten-188 .191 .00270 64.1 1 1 .173 Tungsten-187
Californium-252 2.64 2.64 2.49 1 .0673 .168 Curium-248
Osmium-194 6.0 .00343 38.04 1 1 .130 Osmium-193
Technetium-99 211000 211000 .132 .903 1 .119 Technetium-99
Strontium-90 28.9 .138 .420 1 1 .0580 Strontium-89
Tungsten-181 .332 .332 60 .0012 1 .0239 Tungsten-181
Promethium-145 17.7 .931 .7 .0308 1 .022 Samarium-145
Samarium-145 .931 .931 .7 .0308 1 .022 Samarium-145
Californium-254 .166 .049 20.0 1 .0151 .0148 Californium-253 1303
Polonium-210 .379 .379 .0338 1 1 .0128 Polonium-210
Iodine-131 .0220 Stable .29 .341 1 .00218 Tellurium-130
Ruthenium-106 1.023 .000507 .390 1 1 .000198 Ruthenium-105
Argon-42 32.9 .000208 .509 1 1 .000106 Argon-41
Silicon-32 153 .000299 .107 1 1 .000032 Silicon-31
Curium-250 8300 .000122 1.60 1 .138 .0000027 Curium-249 10
Lead-210 22.3 .000371 .00143 1 1 .00000053 Lead-209
Caesium-137 30.2 .0360 Unknown 1 1 Caesium-136
Output Output Hurdle Capture Natural Capture Production Hurdle
Half life half life rate
year year barn fraction fraction barn*year
Einsteinium-257 .0211 .000048 Unknown Unknown Einsteinium-256
Einsteinium-259 .0180 .000074 Unknown Unknown Einsteinium-258
Fermium-257 .275 .000300 Unknown Unknown Fermium-256
Subjecting natural europium to neutrons for a short time produces mostly europium-152.
Subjecting natural europium to neutrons for a medium time produces mostly europium-154.
Subjecting natural europium to neutrons for a long time produces 2/3 europium-154 and 1/3 europium-155.
Half life Neutron capture Natural Energy Gamma max Decay
year barn fraction MeV MeV
Europium-151 Stable 9100 .478 - -
Europium-152 13.5 11800 0 1.86 1.408
Europium-153 Stable 312 .522 - -
Europium-154 8.59 1663 0 1.968 1.274
Europium-155 4.76 3843 0 .252 .147
Europium-156 .0416 100 0
Europium-157 .00174 0
Thulium-169 Stable 105.6 1 -
Thulium-170 .352 87.6 0 .968 β
Thulium-171 1.91 9.90 0 .096 β
Promethium-143 .725 3.07 0 β+
Promethium-144 .994 15.09 0 β+
Promethium-145 17.7 5.28 0 .164 .072 EC
Promethium-146 5.53 8.41 0 1.495 1.189 EC
Promethium-147 2.623 167.2 0 .224 .224 Β 72 barn to Pm-148m. 82 barns to Pm-148
Promethium-148 .0147 0 β
Promethium-148m .113 0 β
Neodymium-142 Stable 18.7 .272
Neodymium-143 Stable 337 .112
Neodymium-144 Stable 3.6 .238
Neodymium-145 Stable 42 .0829
Neodymium-146 Stable 1.4 .172
Neodymium-147 .0301 142.9 0 β
Neodymium-148 Stable .0575
Neodymium-149 .000194 0 β
Neodymium-150 Stable .0563
Samarium-144 Stable .7 .0308
Samarium-145 .931 280.3 0 .617 .061 EC
Samarium-146 68000000 .382 0
Samarium-147 Stable 57 .150
Samarium-148 Stable 24 .112
Samarium-149 Stable 42080 .138
Samarium-150 Stable 104 .0737
Samarium-151 90 14070 0
Samarium-152 Stable 206 .267
Samarium-153 .00528 0
Samarium-154 Stable 8.4 .227
Making transuranics takes many neutrons. Also, fission can halt the process. When going from uranium-238 to californium-251, the fraction of isotopes that make it to californium-251 is .0000151.
There are no hurdles with short half lives until fermium-258, with a half life of .000370 seconds.
The sequence for making transuranics is:
Half life Fission Capture Capture Cumulative Decay
year barn barn fraction fraction
Uranium-238 4470000000 .000010 2.68 1 1 α
Plutonium-239 14100 748 1017 .58 .58 α
Plutonium-240 6561 .030 290 1 .58 α
Plutonium-241 14.3 937 363 .28 .16 β
Plutonium-242 373000 .0026 18.5 1 .16 α
Americium-243 7370 .2 75.3 1 .16 α
Curium-244 18.1 1.1 13 .92 .16 α
Curium-245 8500 2161 383 .151 .147 α
Curium-246 4730 .17 1.36 .89 .0222 α
Curium-247 15700000 82 58 .41 .0198 α
Curium-248 340000 .34 2.49 .88 .00811 α
Californium-249 351 1666 483 .22 .00714 α
Californium-250 13.08 112 1701 .94 .00157 α
Californium-251 900 4894 2849 .37 .00148 α
Californium-252 2.64 33.0 20.4 .38 .000546 α
Californium-253 .049 1303 19.95 .0151 β
Californium-254 .166 2.001 4.51 .69 Fission
Einsteinium-255 .109 .503 55.4 1 β
Fermium-256 .000300 Unknown Unknown Unknown α
Fermium-257 .275 2951 3.003 .00102 α
Fermium-258 .000370 Unknown Unknown Unknown Fission
Fermium-259 1.5 Unknown Unknown Unknown Fission
Fermium-260 .004 Unknown Unknown Unknown Fission
A neutron could either be captured or it could trigger fission. "Capture fraction" is the fraction of capture events.
"Cumulative fraction' is the product of capture fractions up to the given isotope.
Energy per neutron = E = 200 MeV/neutron Neutron mass = M = 1.67e-27 kg Neutron energy/mass = e = E/M = 1.9e16 Joule/kg Electricity energy/$ = L = 30 MJoule/$ Neutron price/kg = P = e/L = 640 M$/kg
A neutron can turn uranium-238 into plutonium-239. The energy cost of plutonium-239 is 2.7 M$/kg.
Actinides beyond plutonium take many neutrons to make. It takes 14 neutrons to get from uranium-238 to californium-252.
A calutron separate isotopes with a magnetic field.
Protons Price/kg World produce America stockpile Natural fraction
M$/kg kg/year kg
1 Hydrogen-2 .004 1000000 .00015
1 Hydrogen-3 30 10 30 0
2 Helium-3 1 10 30 .000002
2 Helium .000024 50000000
3 Lithium .000070 36000000
3 Lithium-6 .06 .0759
4 Beryllium .00150 425000 All beryllium-9
4 Beryllium-7 0
5 Boron-10 .20
6 Carbon-12 .12 .989
6 Carbon-14 .000000000001
21 Scandium-46
27 Cobalt-60
38 Strontium-90 .01
55 Caesium-137
63 Europium-152
63 Europium-154
77 Iridium-192
77 Iridium-192m
84 Polonium-209 50000000
84 Polonium-210
88 Radium-226 .1 0 30
88 Radium-228 .1 0 30
89 Actinium-227 1
90 Thorium .000290 10000000
90 Thorium-228
90 Thorium-229
90 Thorium-230
90 Thorium-231
91 Protactinium-231 .28
92 Uranium .000101 70000000
92 Uranium-230
92 Uranium-232
92 Uranium-233 2000
92 Uranium-235 .1 480000 .0072
93 Neptunium-237 .66
94 Plutonium-238
94 Plutonium-239 6.5 80000
95 Americium-141 .7 10
95 Americium-142m
95 Americium-143 .7 10
95 Curium-242 1 10
95 Curium-243
95 Curium-244 185 .17 10
95 Curium-245
95 Curium-246
95 Curium-247 .1
95 Curium-248 160000 .0001
96 Curium-250
97 Berkelium-249 185000 .020 N/A
98 Californium-249 185000 .0005
98 Californium-250
98 Californium-251
98 Californium-252 60000 .5 N/A
99 Einsteinium-253 .01 N/A
99 Einsteinium-254 .000001 N/A
100 Fermium-257
Power Power Distance
Watts Sun=1 light year
Human civilization, 1800 6.0e11
Human civilization, 1900 1.3e12
Human civilization, 2023 2.0e13
Solar power hitting Earth 1.7e17
Sun 3.8e26 1 0
Star Sirius 9.7e27 25.4 8.6
Star Aldebaran 2.0e29 520 65
Star Spica 7.8e30 20500 280
Star Naos 3.1e32 813000 1080
Star eta Carine 1.7e33 4600000 7500
Milky Way central region 1 e35 26000 Stars within 10 light years of the center
Galacy Centaurus A AGN 11000000 Nearest active galactic nucleus
Milky Way total 5 e36 -
Virgo central galaxy 5 e37 53500000
Quasar Markarian 231 1.4e39 581000000 Nearest quasar
Quasar Ton 618 4 e40 18200000000 Brightest quasar
Galaxy W2246-0526 1.3e41 12600000000 Brightest galaxy
Isotopes that decay by alpha and don't produce betas or gammas have value because they can be around humans. The pure alpha isotopes are:
Half life Power/Mass Obtainable by
year Watt/kg neutron transmutation
Fermium-257 .275 * Fm257 -> Es253 -> Bk249
Polonium-210 .379 144000 *
Curium-242 .446 124000
Polonium-208 2.898
Curium-244 18.1 2823 * Cm242 -> Pu240 -> U236
Curium-243 29.1 1885 * Cm243 -> Pu239 -> U235
Gadolinium-148 75 800
Plutonium-238 87.7 578 *
Polonium-209 125.2 Po209 -> Pb205 -> Tl205 The electron capture has a half life of 15 Myr
Americium-241 432 114 *
A nuclear reactor needs materials with a low neutron capture cross section. Zirconium is the favored structural metal.
Neutron capture Natural Neutron Density Atom Stopping
fraction scatter density power
barn barn g/cm3
Oxygen .00028 -
Carbon .0035 -
Helium .007 -
Beryllium .0092 -
Bismuth .034 -
Neon .04 -
Magnesium .063 -
Lead .171 -
Zirconium .184 -
Aluminum .232 -
Hydrogen .332 -
Niobium 1.15 -
Ruthenium 2.56 -
Molybdenum 2.6 -
Nickel 4.49 -
Platinum 10 -
Osmium 15 -
Tungsten 18.3 -
Tantalum 20.6 -
Hafnium 104 -
Hydrogen-3 0 0 2.178
Helium-4 0 1.000 .961 .145 .036 .036
Carbon-14 .000000310 0 3.152 4.11 .294 .93
Nitrogen-15 .000024 .004 5.293
Beryllium-10 .000100 0 6.291 2.06 .206 1.30
Oxygen-18 .000141 .00205 3.987
Oxygen-16 .000190 .998 4.498
Lead-208 .000230 .524 12.94 11.34 .055 .72
Hydrogen-2 .000550 .000145 4.705
Carbon-13 .00137 .011
Carbon-12 .00389 .989
Boron-11 .00508 .80
Beryllium-9 .0076 1 1.85
Zirconium-90 .0107 .514
Magnesium-26 .0382 .110
Lithium-7 .0454
Molybdenum-92 .0614 .146
Ruthenium-106 .146 0
Titanium-50 .179 .0518
Aluminum-27 .231 1
Oxygen-17 .244
Hydrogen-1 .333 .9999 32.81
Chromium-54 .36 .0236
Platinum-196 .72 .253
Iron-58 1.28 .0028
Nickel-64 1.52 .00926
Osmium-192 3.12 .41
Tungsten-183 10.1 .143
Hafnium-180 12.92 .351
Tantalum-181 20.5 .999
The best isotope for neutron shielding is gadolinium-157, with a neutron capture cross section of 259000 barns. Natural gadolinium is a mix of isotopes with an overall cross section of 49000 barns.
Elements and isotopes with a high neutron capture cross section are:
Neutron capture Price/kg Quality
barns $/kg barns/$
Gadolinium 49000 29 2450
Samarium 5922 13.6 740
Europium 4600 287 15
Cadmium 2450 2.7 1220
Boron 767 3.7 183
Lithium 70.5 70 .35
Xenon-135 2650000 Half life = .00104 year
Zirconium-88 861000 Half life = .228 year
Gadolinium-157 259000
Gadolinium-155 61100
Beryllium-7 56800
Samarium-149 42080
Cadmium-113 30000
Europium-151 9100
Helium-3 5333
Boron-10 3835
Lithium-6 940
Neutrons can be generated by bombarding beryllium-9 with alpha particles.
α + Beryllium-9 → Carbon-12 + Neutron
 |
|---|
Half life Decay Gamma energy Obtainable by neutron transmutation
year MeV
Antimony-124 .165 Beta 2.09 Most gammas are 1.69 MeV. Max 2.09 MeV
Cobalt-60 5.26 Beta 1.33 *
Sodium-22 2.6 Beta+ 1.28
Hafnium-178m 31 Gamma .507 *
 |
|---|
Lithium-6 + Neutron → Helium-4 + Tritium Cross section of 940 barns
Half life Obtainable by
year neutron transmutation
Fluorine-18 .000209
Molybdenum-99 .00752 * Decays to Technetium-99m, which has a half life of 6.01 hours
Thallium-201 .00832
Iodine-131 .022 *
Iodine-125 .0362
Palladium-103 .0465 *
Strontium-82 .0694 Decays to Rubidium-82
Iridium-192 .202 *
Strontium-89 *
Samarium-153 *
Rhenium-186 *
Lutetium-177 *
Bismuth-213 *
Lead-212 *
Radium-223
Boron-10 Stable Natural
Gadolinium-157 Stable Natural
 |
|---|
Some isotopes undergo 5 or 6 alpha decays, such as uranium-232. This is the red line in the plot.
U-232 → Th-228 → Ra-224 → Rn-220 → Po-216 → Pb-212 → Bi-212 → Po-212 → Pb-208
The double-decay nuclei with half lives between 1 month and 100 years are:
1st decay 2nd decay Total 1st 2nd Obtainable by neutron transmutation
half life half life energy energy energy
year year MeV MeV MeV
Osmium-194 → Ir-194 → Pt-194 6.02 .00022 2.330 .096 2.234 *
Tungsten-188 → Re-188 → Os-188 .191 .00194 2.469 .349 2.120 *
Rhenium-184m → Re-184 → Os-184 .463 .104 .646 .188 .458 *
Hafnium-172 → Lu-172 → Yb-172 1.87 .0283 1.835 .338 1.497
Fermium-247 → Es-253 → Cm-249 .275 .0560 *
Rhodium-102m → Rh-102 → Ru-102 3.742 .567 1.509 .141 1.268
Einstein-254 → Cf-250 → Cm-246 .755 13.3 *
Titanium-44 → Sc-44 → Ca-44 59.1 .00046 3.798 .146 3.652
Strontium-90 → Y-90 → Zr-90 28.9 .00731 2.826 .546 2.280 *
Iridium-192m → Ir-192 → Pt-192 241 .202 1.615 .155 1.460 *
Tin-121m → Sn-121 → Sb-121 43.9 .00308 .396 .0063 .390 *
Argon-42 → K-42 → Ca-42 32.9 .00141 4.124 .599 3.525 *
Silicon-32 → P-32 → S-32 153 .0391 1.919 .21 1.709 *
Germanium-68 → Ga-68 → Zn-68 .742 .000129
 |
|---|
Melt Boil Density
Zirconium 2128 4650
Niobium 2750 5017
Molybdenum 2896 4912
Technetium 2430 4538
Ruthenium 2607 4423
Rhodium 2237 3968
Lutetium 1925 3675
Hafnium 2506 4876 13.3
Tantalum 3290 5731 16.7
Tungsten 3695 6203 19.2
Rhenium 3459 5309 21.0
Osmium 3306 5285 22.6
Iridium 2719 4403 22.6
Platinum 2041 4098 21.4
Thorium 2023 5061
Protactinium 1810 4300
Uranium 1405 4404 19.1
Neptunium 912 4447
Curium-240 produces 2 alphas with short half lives and becomes Uranium-232, which has a long half life. Uranium-232 produces an alpha with a long half life and then 5 more alphas with short half lives. It can be used as an alpha rocket, where the first two decays give it a fast launch, and the remaining decays power it for a long time. The decay sequence of Curium-240 is:
Half life
year
Curium-240 .0739 Alpha
Plutonium-236 2.858 Alpha
Uranium-232 68.9 Alpha
Thorium-228 1.912 Alpha
Radium-224 .00986 Alpha
Radon-220 .0000018 Alpha
Polonium-216 .000000005 Alpha
Lead-212 .00121 Alpha
Bismuth-212 .00012 Beta
Tellurium-208 .0000057 Alpha
Lead-208 Stable Beta
Cross sections for fusion neutrons at 14.1 MeV, in millibarns. All columns are fusion neutrons except the last column, which is fast fission neutrons. For fusion neutrons, the usual outcome is for neutrons to be subtracted from the target nucleus.
Thorium is more likely to lose neutrons than uranium.
(n,2n) (n,3n) (n,fission) (n,inelastic) (n,G) (n,2n)
fission
Actinium-227 2170 353 62.8 445 1.119 15.87
Thorium-228 1897 85.8 598 498 1.23 7.39
Thorium-229 1717 92.7 864 346 1.19 33.5
Thorium-230 1856 244 564 424 .96 12.2
Thorium-231 1685 336 658 349 1.21 42.7
Thorium-232 1786 522 361 468 1.14 16.8
Uranium-320 174 .0126 2518 416 .78 .138
Uranium-321 75 .000028 2474 403 .69 2.08
Uranium-322 401 .77 2570 420 .82 .760
Uranium-233 181 .271 1.84 368 .58 1.84
Curium-242 231 .120 2907 359 1.19 .921
The prompt kinetic energy released by fission is:
Fission energy (MeV)
Actinium 168
Thorium 172
Protactinium 177
Uranium 181
Neptunium 185
Plutonium 189
Americium 195
Curium 198
Berkelium 203
Californium 207
 |
|---|
There is a hypothetical "island of stability" around atomic number 112 where nuclei may be long-term stable. A second island may exist at atomic number 126.
Experiments can only measure the longest-lived isotope up to a proton number of 105, and beyond that we plot theory. Theoretical half lives are uncertain by an order of magnitude.
 |
|---|
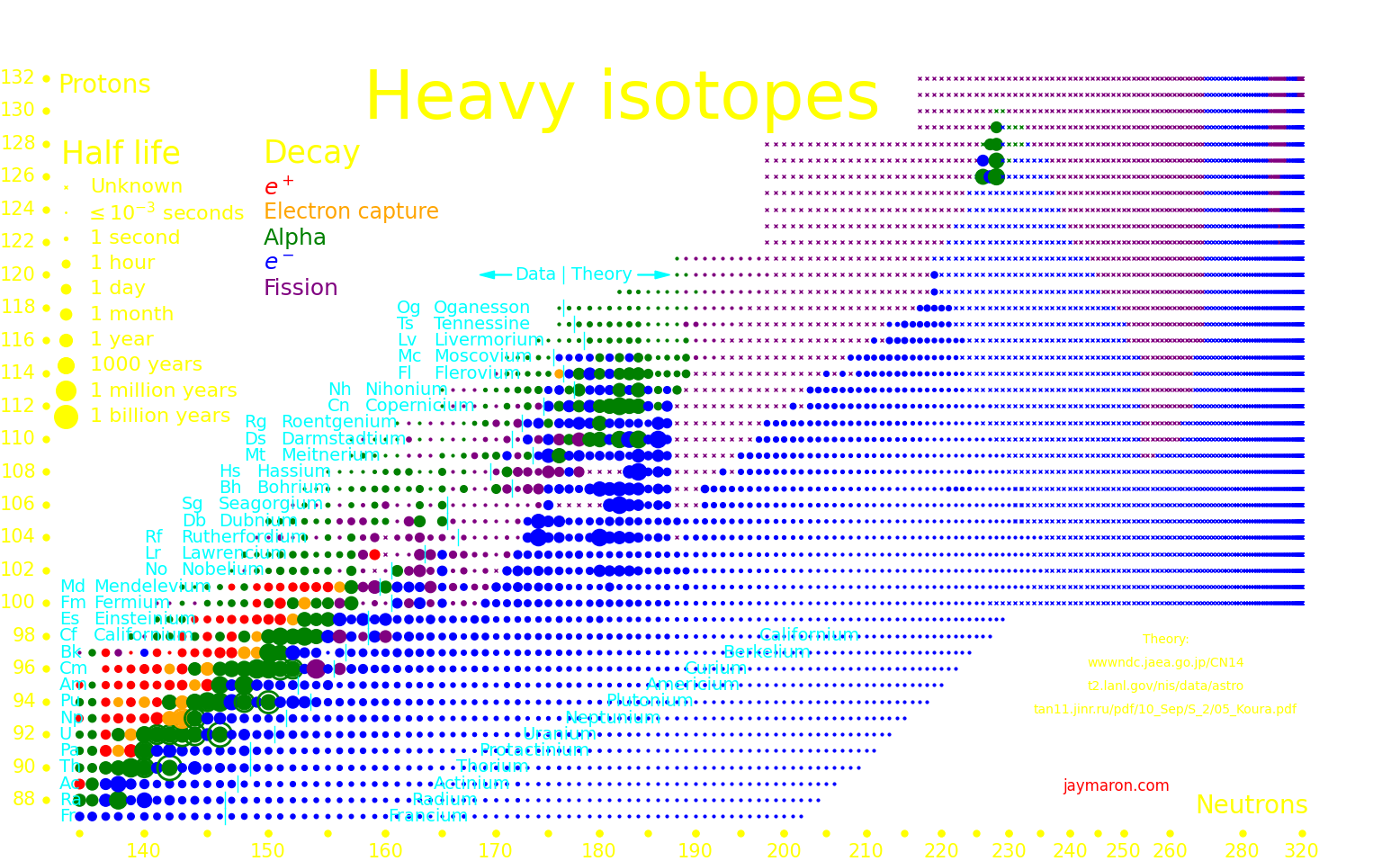 |
|---|
It's possible that for large nucleon number, larger than around 300, that the nucleus transitions to a lower-energy state, called "Up down quark matter", or "udQM". The existence of udQM is unresolved. Theory is uncertain, and it hasn't been experimentally produced. The largest nucleus that's been produced is oganesson-294, with 118 protons and 294 nucleons. It shows no sign of udQM, so if udQM exists, it's beyond oganesson.
If udQM nuclei exist, they could potentially be long-term stable. They don't fission because it would take the nucleus to a higher-energy state. They decay by alpha until they're too light to be udQM, at which point they fission.
If udQM nuclei exist, then there may exist long-lived elements from Z=140 to way beyond. These are "continental elements".
The largest nucleus that standard nuclei can make has Z=140. Nuclei larger fission instantly. The only way that nuclei with Z>140 can exist is if udQM exists.
In the isotope table, we use experimental data from Wikipedia if it exists, otherwise we use theory from https://wwwndc.jaea.go.jp/CN14 and https://t2.lanl.gov/nis/data/astro. Nobel gases have a closed shell of electrons, and the shell numbers are called "magic numbers". The magic numbers for electron shells are:
Helium 2 Neon 10 Argon 18 Krypton 36 Xenon 54 Radon 86 Oganesson 118
The magic numbers for neutrons are 2, 8, 20, 28, 50, 82, 126, 184. The magic numbers for protons are the same as for neutrons, up to 82, and the next proton magic numbers are 114, 126, 154, and 164. Nuclei that are magic for both protons and neutrons are:
Protons Neutrons
Helium-4 2 2
Oxygen-16 8 8
Calcium-40 20 20
Calcium-48 20 28
Lead-208 82 126
Flevorium-298 114 184 Undiscovered
Unnamed 126 216 Undiscovered
Unnamed 126 228 Undiscovered
Unnamed 154 308 Undiscovered
Unnamed 164 308 Undiscovered
Unnamed 164 318 Undiscovered
Unnamed 164 406 Undiscovered
The nuclei from helium-4 to lead-208 are stable.
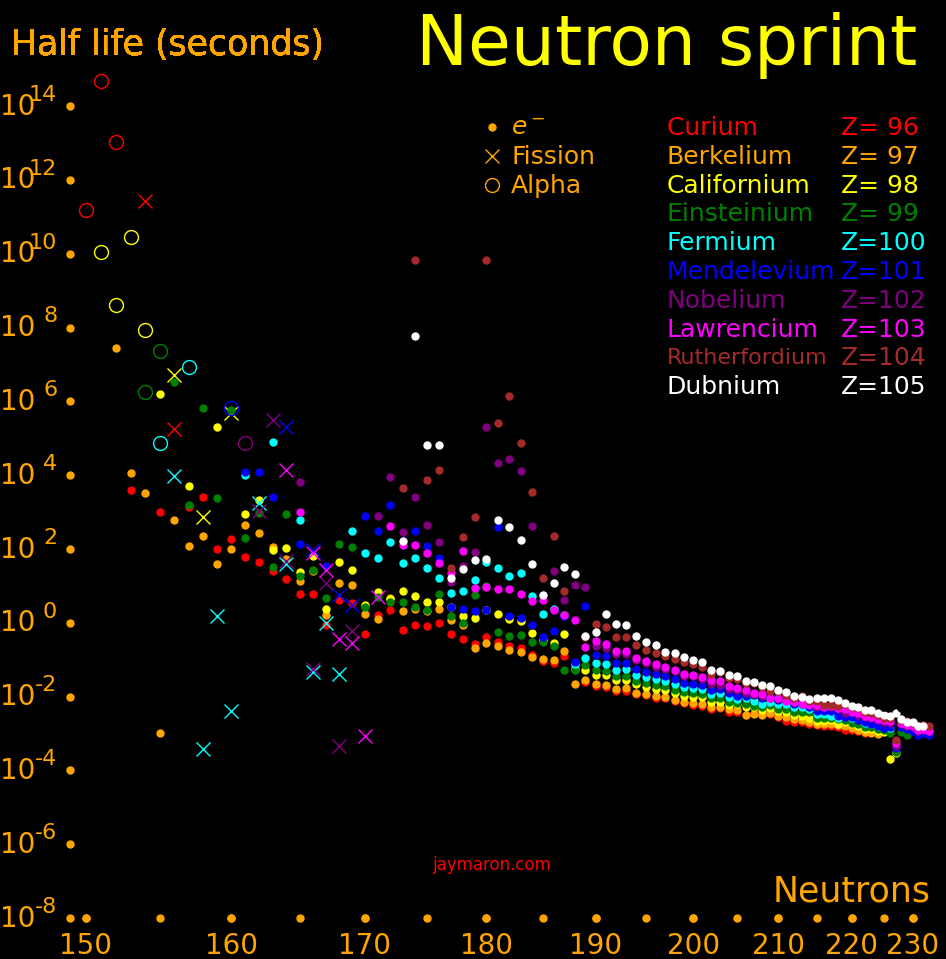 |
|---|
A Fermi gas with a Fermi energy of 335 neV has a density of 1.39e23 particles/meter3
Fermi number density = n = 16π/3 λ-3= 1.39e23 particles/meter3
Fermi wavelength = λ = 4.94e-8 meter
Fermi momentum = Q = 1.34e-26 kg*meter/second
Planck constant = h = Q ℏ = 6.626e-34 Joule*second
Fermi energy = E = Q2/(2m) = ℏ2/(2m) (3π2n)2/3
= 335 neV
Neutron mass = m = 1.675e-27 kg
 |
|---|
Full list.
Half life Heat Decay Electron Elect Gamma Form rate Obtainable Decay
max ave max by neutron
year Watt/kg MeV MeV MeV MeV barn*year transmute
Neutron .000027 .782 .782 * β Half life = 879 seconds
Einsteinium-253 .0560 * α
Tungsten-188 .191 19920 .349 8.49 * 2β
Californium-254 .166 11200000 207 .0102 * Fission
Iridium-192 .202 77147 1.460 134 * β
Scandium-46 .229 460000 2.366 .357 .112 1.121 .38 * β
Sulfur-35 .239 .167 .0488 * β
Fermium-247 .275 * α
Tantalum-182 .313 65260 1.814 4.45 * β
Tungsten-181 .332 59100 1.732 .0166 * EC
Thulium-170 .352 11800 .968 .968 .968 37.2 * β M 73% e- .968 MeV. 22% e- .884 MeV & .084 MeV gamma
Polonium-210 .379 139000 5.41 0 .0089 * α M
Calcium-45 .445 .257 .257 .257 * β
Curium-242 .446 * α
Gadolinium-153 .658 .484 .173 * EC
Zinc-65 .668 63900 1.352 .21 * β+
Einsteinium-254 .755 * α
Samarium-145 .931 * EC
Ruthenium-106 1.023 67700 3.584 .00014 * 2β
Cadmium-109 1.267 * EC
Thulium-171 1.91 .0965 30.8 * β
Caesium-134 2.06 15300 2.059 21 * β
Promethium-147 2.6 1200 .224 .86 * β
Californium-252 2.64 41400 12.33 0 * α 96.9% (6.12 Mev). Fission 3.09% (207 MeV)
Iron-55 2.74 3140 .231 .091 * EC
Thallium-204 3.78 .766 * β
Europium-155 4.76 705 .252 * β
Cobalt-60 5.27 18300 2.82 1.39 * β
Promethium-146 5.5 1.495 * EC 66%, e- 34%
Osmium-194 6.02 4313 2.330 .090 * 2β
Europium-154 8.59 3049 1.968 216 * β
Barium-133 10.51 758 .517 .0049 * EC
Tritium 12.33 1031 .0186 .0186 .0057 49 * β
Europium-152 13.5 1858 1.86 6005 * β & EC
Californium-250 13.08 * α
Cadmium-113m 14.1 340 .264 * β
Plutonium-241 14.3 3050 4.90 * β
Promethium-145 17.7 131 .164 * EC
Curium-244 18.1 * α
Lead-210 22.3 2907 9.100 0 .00000037 * α
Strontium-90 28.9 460 2.826 .29 * β, β M
Curium-243 29.1
Caesium-137 30.1 583 1.176 * β
Hafnium-178m2 31 930 2.446 * γ
Argon-42 32.9 .599 * β
Tin-121m 43.9 153 .396 .088 * IT, β
Platinum-193 50 17.5 .057 6.93 * EC
Plutonium-238 87.7 578 5.59 0 .125 * α
Samarium-151 90.0 11.6 .077 34 * β
Nickel-63 100.1 5.52 .066 .066 .017 .066 9.96 * β
Americium-242m 141 725 12.33 0 5.8 * 2α
Silicon-32 153 804 1.92 2.22 * β, β
Iridium-192m2 241 72 1.628 69 * β
Argon-39 269 .566 * β
Californium-249 351 * α
Americium-241 432.2 114 * α M
Californium-251 900 * α
Curium-246 4760 * α
Carbon-14 5730 3.99 .156 .156 .049 * β
Plutonium-240 6561 5.256 * α
Americium-243 7370 * α+β
Curium-250 8300 170 148 .000019 * Fission 74%, Alpha 18%, Beta 8%
Curium-245 8500 * 2α+β
Plutonium-239 24110 * α
Technetium-99 211000 .003 .294 * β
Curium-248 348000 * α
Plutonium-242 375000 * α
Beryllium-10 1390000 .556 * β
Technetium-97 4200000 * EC
Technetium-98 4200000 * β
Curium-247 15600000 * 3α+2β
Uranium-236 23420000 * α
Plutonium-244 81300000 * 3α+2β
Thorium-227 .0512 9194000 36.14 5α+2β
Uranium-230 .0554 9280000 6α+2β
Thorium-228 1.912 235000 34.784 5α+2β
Radium-228 5.75 90660 40.198 5α+4β
Actinium-227 21.8 21600 36.18 5α+3β
Uranium-232 68.9 7545 40.79 6α+2β
Radium-226 1599 286 34.958 5α+4β
Thorium-229 7917 57.7 35.366 5α+3β
Protactinium-231 32600 16.2 41.33 6α+3β
Thorium-230 75380 6.78 39.728 6α+4β
Uranium-233 159200 * 6α+2β
Uranium-234 245500 7α+4β
Neptunium-237 2144000 8α+4β
Curium-247 15600000 * 3α+2β
Uranium-235 703800000 * 7α+4β
Uranium-238 4468000000 .00010 51.771 * 8α+6β
Thorium-232 14050000000 47.655 * 6α+2β
Mendelevium-260 .076 Fission
Mendelevium-258 .141 α
Beryllium-7 .146 1822000 .547 EC
Cobalt-56 .212 β+
Rhenium-184m .463 16000 IT, β
Thulium-168 .255 β+
Gold-195 .510 .227 .210 EC
Cobalt-57 .744 .836 .137 EC
Manganese-54 .855 64400 EC
Vanadium-49 .901 .602 EC
Californium-248 .913 α
Einsteinium-252 1.29 0 α, EC
Lutetium-173 1.37 .630 EC
Tantalum-179 1.82 1.060 EC
Plutonium-236 2.858 α
Hafnium-172 1.87 11700 1.835 EC
Sodium-22 2.6 68700 2.842 β+ or EC
Polonium-208 2.99 0 α
Rhodium-101 3.3 EC
Lutetium-174 3.31 β+
Rhodium-102m 3.742 β+
Rhodium-101 4.07 9890 1.980 EC
Niobium-93m 16.1 IT
Bismuth-207 31.55 2.397 β+
Europium-150 36.9 2.259 β+
Titanium-44 59.1 4318 3.798 EC, β+
Terbium-157 71.0 11.0 .060 β+
Gadolinium-148 75 800 0 α
Polonium-209 125.2 0 α
Terbium-158 180 β+
Iridium-192m2 241 IT, β
Holmium-163 4570 EC
Darmstadtium-293 37.7 58900 220 β+fission Theoretical
Darmstadtium-292 133 16700 220 α+fission Theoretical
Copernicium-294 355 6230 220 α+fission Theoretical
Darmstadtium-294 380 5820 220 α+fission Theoretical
Argon-37 .0824 .814 0 * EC
Argon-39 269 * β
Argon-42 32.9 * β
Krypton-85 10.78 * β
Xenon-127 .0994 .662 0 .618 * EC
Half life Heat Decay Electron Elect Gamma Form rate Obtainable Decay
max ave max by neutron
year Watt/kg MeV MeV MeV MeV barn*year transmute
A neutron has a half life of 610.1 seconds and a decay energy of .782 MeV.
Full list.
Half life Power/mass Decay Gamma Formation Obtainable by Decay
energy max rate neutron
year Watt/kg MeV MeV barn*year transmutation
Nickel-63 100.1 5.52 .017 .017 2.5 * β
Tritium 12.33 315 .0186 .0186 71 * β
Rubidium-83 .236 .910 .0322 0 EC
Arsenic-73 .220 .341 .0534 0 EC
Terbium-157 71.0 11.0 .060 .054 0 EC
Samarium-145 .931 .617 .061 .022 * EC
Tantalum-179 1.82 .110 .065 0 EC
Promethium-145 17.7 131 .164 .072 .022 * EC
Samarium-151 90.0 11.6 .077 .077 * β
Platinum-193 50 17.5 .057 .076 3.81 * EC
Cadmium-109 1.26 .216 .088 .57 * EC
Thulium-171 1.91 606 .096 .096 30.8 * β
Gadolinium-153 .658 .484 .100 * EC
Iron-55 2.74 3140 .231 .126 .36 * EC
Cobalt-57 .744 .836 .136 0 EC
Europium-155 4.76 705 .252 .147 312 * β
Cerium-139 .377 .278 .166 * EC
Gadolinium-153 .658 .484 .173 * EC
Gold-195 .510 .227 .210 EC
Promethium-147 2.6 1200 .224 .224 1.3 * β
Calcium-45 .445 .257 .257 * β
Rhodium-101 3.3 9890 .541 .325 0 EC
Europium-149 .255 .692 .328 0 EC
Barium-133 10.51 758 .517 .384 * EC
Tin-121m 43.9 153 .396 .390 .01 * IT & β
Beryllium-7 .146 .862 .478 0 EC
Vanadium-49 .901 232 .602 ? 0 EC
Making radium from polonium needs extreme neutron flux. The hurdle is polonium-212 with a half life of 249 nanoseconds. Once you have radium, it's easy to get to thorium.
Half life Neutron capture Decay
second barn
Bismuth 209 Stable .0338
Bismuth 210 433000 e-
Bismuth 211 130 alpha
Polonium 210 12000000 .00123 alpha
Polonium 211 .516 alpha
Polonium 212 .000000249 alpha
Polonium 213 .00000365 alpha
Polonium 214 .000164 alpha
Polonium 215 .00178 alpha
Polonium 216 .145 alpha
Polonium 217 1.47 alpha 95%, beta 5%
Polonium 218 186 alpha
Polonium 219 618 beta 71.8%, alpha 28.2%
Polonium 220 40 beta
Polonium 221 132 beta
Polonium 222 546 beta
Polonium 223 6 beta
Polonium 224 180 beta
Polonium 225 10 beta
Polonium 226 60 beta
Polonium 227 2 beta
Astatine 217 .0323 alpha
Astatine 218 1.27 alpha
Astatine 219 56 alpha 97%, beta 3%
Astatine 220 223 beta 92%, alpha 8%
Astatine 221 138 beta
Astatine 222 54 beta
Astatine 223 50 beta
Astatine 224 150 beta
Astatine 225 3 beta
Astatine 226 420 beta
Astatine 227 5 beta
Astatine 228 60 beta
Astatine 229 1 beta
Radon 225 280 beta
Radon 226 444 beta
Radon 227 20.8 beta
Radon 228 65 beta
Radon 229 12 beta
Radon 230 ? beta
Radon 231 ? beta
Francium 228 38 beta
Francium 229 50.2 beta
Francium 230 19.1 beta
Francium 231 17.6 beta
Francium 232 5 beta
Francium 233 .9 beta
Radium 223 988000 alpha
Radium 224 314000 alpha
Radium 225 1290000 beta
Radium 226 1600 year alpha
Radium 227 2550 beta
Radium 228 182000000 beta
Radium 229 240 beta
Radium 230 5580 beta
Radium 231 103 beta
Radium 232 250 beta
Radium 233 30 beta
Radium 234 30 beta
Many light isotopes fission with slow neutrons.
Natural Half Neutron Neutron capture Decay mode
fraction life capture output
years barn
Hydrogen-1 .99985 Stable .3326 Deuterium
Hydrogen-2 .00015 Stable .000519 Tritium
Hydrogen-3 0 12.32 0 - β
Helium-3 .000002 Stable 5333 Tritium
Helium-4 .99999 Stable 0 -
Lithium-6 .0759 Stable 940 Helium-4 + Tritium
Lithium-7 .9241 Stable .0454 Helium-4 + Helium-4
Beryllium-7 0 .146 56800 Lithium-7 Electron capture
Beryllium-8 0 e-16 α
Beryllium-9 1 Stable .0076 Beryllium-10
Beryllium-10 0 1510000 .00010 Boron-11 β
Boron-11 .20 Stable 3835 Lithium-7 + Helium-4
Boron-12 .80 Stable .0055 Carbon-12
For a neutron in a material, the collision length is
Density of nuclei in the material = ρ Cross section of nuclei in the material = σ Neutron collision length = X = 1/(ρσ)
Suppose the neutrons are in thermal equilibrium with nuclei in the material, and that there's a bulk speed between neutrons and the material of V.
Neutron bulk speed = V Neutron thermal speed = Vn Neutron interaction speed = Vi = (Vn2 + V2)½ Between neutrons and the material Neutron collision time = T = X/Vi
Neutrons feel a characteristic acceleration of
Characteristic acceleration = A = V/T = V Vi ρ σ
The cross section is a function of the characteristic collision speed.
Thermal speed of nuclei in the material = Vm Characteristic collision speed = Vc = (Vn2 + Vm2 + V2)½ Between neutrons and the material
For high speed, σ is a constant of speed, and for low speed, σ times speed is constant.
 |
|---|
 |
|---|
For a degenerate gas,
Energy total = E
Volume = V
# of particles in the volume = N
Particle number density = n = N/V
Particle mass = m
Density = ρ = mN/V
Pressure of a monatonic gas = P = ⅔ E/V
Fermi pressure = PF = ⅔ PF5/(10π2mℏ3)
= 3⅔ 5-1 π4/3 ℏ2 m-1 ρ5/3
Neutron source
Moderator, beryllium-10
Moderator, liquid nitrogen
Moderator, liquid deuterium
Moderator, liquid helium-4
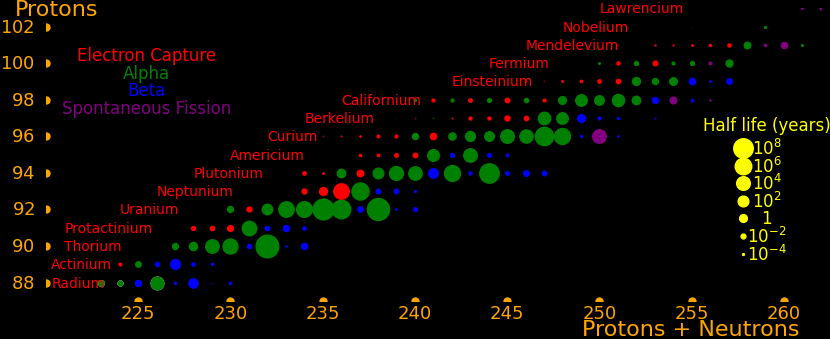 |
|---|
The actinides are the elements from actinium to lawrencium. None are stable but many are long-lived.
 |
|---|
Neutron capture transmutes an isotope one space to the right and beta decay transmutes an isotope one space up.
The most massive nuclei that exist naturally are thorium-232, uranium-235, or uranium-238. All are unstable but have half lives larger than 700 million years. The road starts with these isotopes and then adding neutrons transmutes them according to the orange lines. The road forks at beta isotopes, which can either beta decay or capture a neutron.
The end of the road is fermium. Neutrons can't further increase the proton number because no fermium isotopes on the road beta decay. The road goes as far as fermium-258, which has a half life of .00037 seconds and spontaneously fissions. Producing heavier isotopes requires an accelerator or an extreme neutron flux (such as occurs in a fission bomb).
Most of the long-lived isotopes are on the neutron road, the most significant exceptions being neptunium-236 and berkelium-247. These isotopes can be reached by alpha decay, which moves an isotope 2 spaces down and 4 to the left.
Americium-242m (half live 141 years) is an excited state of Americium-242 (half life .0018 years) with a high thermal neutron capture cross section.
The thermal neutron capture cross section of Americium-241 to Americium-242 is 748 barns, and to Americium-242m is 83.8 barns.
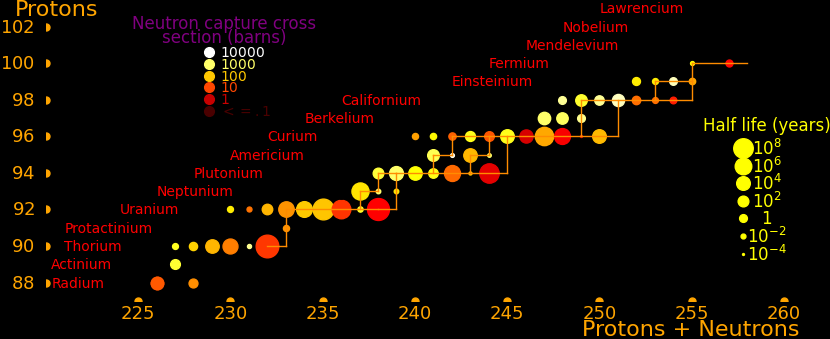 |
|---|
Transmutation rate is proportional to the neutron capture cross section. In order to move rightward on the road the isotope has to have a large neutron capture cross section and it has to have a large half life. This is true everywhere on the road except for curium-249, and so all the long-lived isotopes on the road are easily created, except for curium-250.
The road has a bottleneck at curium-246, which is the isotope with the lowest capture cross section (1.36 barns). The capture cross section of curium-248 is also low (2.49 barns). Traffic slows down here and all the isotopes further down the road have to wait for curium-246 and curium-248.
To create curium-250 you start with curium-248 and add a neutron to produce curium-249. Curium-249 has a half life of 64 minutes and you have to hope it captures a neutron before the decay.
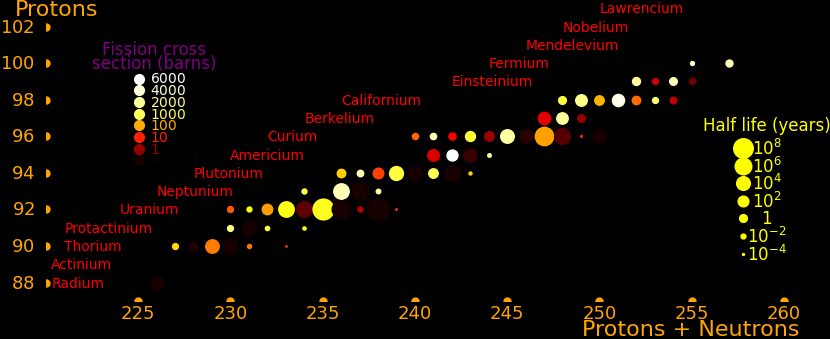 |
|---|
The fission cross section is for thermal neutrons with a Maxwellian spectrum centered at .025 eV. The isotopes with large fission cross sections are:
Thermal Critical Half life
neutron mass
fission
barns kg years
Americium-242m 6686 11 141
Californium-251 4801 5.5 900
Einsteinium-254 2900 9.9 .75
Neptunium-236 2800 6.8 154000
Curium-245 2161 10 8500
Californium-249 1665 6 351
Plutonium-241 937 12 14.3
Plutonium-239 748 10 24100
Curium-243 690 8 29.1
Uranium-235 538 52 704000000
Uranium-233 468 15 159200
 |
|---|
 |
|---|
 |
|---|
Fast Crit Crit Half life Fast Fast
neutron mass diam neutrons capture
fission /fission
barns kg cm years barns
Californium-252 2.32 2.73 4.30
Californium-251 1.28 5.46 900 4.56 .63r
Californium-249 1.74 6 351 *
Curium-247 1.86 7.0 *
Neptunium-236 7 154000 *
Curium-243 2.43 8 29.1 3.70 .4
Plutonium-238 1.994 9.5 3.148
Einsteinium-254 9.89 .75 *
Curium-245 1.75 10 8500 4.0 .4
Plutonium-239 1.800 10 24100 3.123
Americium-242m 1.83 10 141 3.53 .6
Plutonium-241 1.648 12 14.3 3.142
Curium-244 1.73 15 3.52 .8
Uranium-233 1.946 15 159200 2.649
Uranium-235 1.235 52 704000000 2.606
Plutonium-240 1.357 40 3.061
Curium-246 1.25 45 3.49 .4
Neptunium-237 1.335 60 2.889 1.8
Berkelium-247 75.7
Plutonium-242 1.127 80 3.07
Americium-241 1.378 60 3.457 2.0
Berkelium-249 192 3.74
Americium-243 .2i 200 3.45 1.8
Einsteinium-254m
Isotopes with a neutron capture cross section of 1 barn or more can be transmuted on a timescale of 10 years. Isotopes with a cross section smaller than this can't be practically transmuted.
To calculate the transmutation rate,
Neutron flux = F = 10-8 neutrons/barn/second Neutron capture = A = 10 barns Transmutation rate = R = FA = 10-7 transmutations/second = 3.2 transmutations/year
 |
 |
|---|---|
If a nucleus is hit with a pulse of neutrons then the probability that a fission occurs is:
Thermal neutron fission cross section = A = 6400 barns = 6.4⋅10-25 meters2 For Americium-242m Neutron pulse magnitude = F = 1020 neutrons/meter2 Fission probability = P = AF = 6.4⋅10-5 fissions
Actinides are useful for:
*) Neutron-induced fission
*) Radioactivity heat
*) Spontaneous fission
All of these properties are useful for spacecraft. The most useful actinides are:
Half life Neutron Spontaneous Radioactivity
fission fission
years barns Watts/kg Watts/kg
Uranium 233 159200 468
235 704000000 538
Plutonium 238 87.7 818
239 14100 748
241 14.3 937 4315
Americium 241 432
242m 141 6686
Curium 243 29.1 690 2666
244 18.1 4014
245 8500 2161
246 4730
247 15700000
248 340000 .64 .81
250 9000 240 241
Berkelium 249 .90
Californium 248 .91 86 86209 Off-road
249 351 1665
250 13.08 158 5778
251 900 4801
252 2.64 31227 58470
253 .049
254 .166 15896000 15897000
Einsteinium 254 .75 2900
Fermium 257 .275 ? 20000 279000
After Before
ppt ppt
U-234 .2
U-235 10.3 33
U-236 4.4
U-238 943 967
Pu-238 .18
Pu-239 5.7
Pu-240 2.21
Pu-241 1.19
Pu-242 .49
Np-237 .43
Am-241 .22
Am-242 .0007
Am-243 .10
Cm-242 .00013
Cm-243 .00032
Cm-244 .024
Fission products 35
Tc-99 .81
Neutron flux (Neutrons/cm2/second)
Power reactor 5e13
High-flux reactor 6e15
Cosmological s-process e16
Cosmological r-process e27
Fission bomb e31
Thermal Fast Crit Crit Half life Slow Fast SF Therm Fast Fast SF SF
neutron neutron mass diam neutr neut neut capt capt inel
fission fission /fiss /fiss /fiss barn barn W/kg neut/s/kg
barns barns kg cm years
Thorium-232 .078 2.16
Protactinium-231 .83 2.457
Uranium-232 80 2.013 3.296 2
Uranium-233 468 1.946 15 159200 2.48 2.649 73
Uranium-234 .407 1.223 2.578 1.8 3.9
Uranium-235 538 1.235 52 704000000 2.42 2.606 2.0 690 .0057
Uranium-236 .042 .594 2.526 1.8 2.3
Uranium-238 .00001 .308 2.601 1.97 2.68 5.51
Neptunium-236 2800 * 7 154000 * *
Neptunium-237 .019 1.335 60 2.54i 2.889 2 1.8 <.05
Neptunium-238 1243 1.45 .0058 2.79i 2.99i .1
Plutonium-237 2100i .124 * *
Plutonium-238 16.8 1.994 9.5 87.7 2.36 3.148 2.28 558 1204000 Alpha
Plutonium-239 748 1.800 10 24100 2.87 3.123 2.9 1017.3 10.1 Alpha
Plutonium-240 .030 1.357 40 6560 3.061 2.189 478000
Plutonium-241 937 1.648 12 14.3 2.92 3.142 36 <.8 Beta
Plutonium-242 .0026 1.127 80 373000 3.07 2.28 805000
Plutonium-243 181i
Plutonium-244 80800000
Plutonium-245 8500
Americium-241 3.1 1.378 60 3.12 3.457 2.0 500
Americium-242 1322i 3.4i .7
Americium-242m 6686 1.83 10 141 3.26 3.53i 2 .6
Americium-243 .2 .2i 200 3.20i 3.45i 1.8
Americium-244 1528i 3.4i * * .9
Americium-244m 1220i 3.4i 3.14i 3.42i .8
Curium-241 2600 2.21 .090
Curium-242 5 1.78 2.54
Curium-243 690 2.43 8 29.1 3.43 3.70i .4
Curium-244 1.1 1.73 15 18.1 2.72? 3.52i 16.2 .8 3.24i(t) Alpha
Curium-245 2161 1.75 10 8500 3.83 4.0 383 .4 Alpha
Curium-246 .17 1.25 45 2.93 3.49i .4 3.19i(t)
Curium-247 82 1.86 7.0 15700000 3.80 * 58 Alpha
Curium-248 .34 1.09 3.13 * .64
Curium-249 1.21
Curium-250 * .67 3.30 *
Berkelium-247 * 75.7
Berkelium-249 1.0 * 192 3.40 3.74i 240
Berkelium-250 959i
Californium-246 3.1
Californium-248 1.32 86
Californium-249 1665 1.74 6 351 4.06 * 3.4 481.4
Californium-250 112 1.49 3.51 * 158
Californium-251 4801 1.28 5.46 900 4.1 4.56 2839 .62 2.216 Alpha
Californium-252 33 2.32 2.73 2.64 4.00i 4.30i 3.75 20.4 31227 Alpha
Californium-253 1138 * * *
Californium-254 2.001j 1.80 .75 3.85 *
Einsteinium-253 2.51 * 4.7 * 15.9M
Einsteinium-254 2900 * 9.89 .75 4.2 *
Einsteinium-254m 1840 * * *
Fermium-244 4
Fermium-246 4
Fermium-254
Fermium-255 3360i * 4 *
Fermium-256 3.63 *
Fermium-257 * * .275 3.87 * 20000
Nobelium-252 4.2
Thermal Fast Critical Diam Half life Slow Fast SF SF Spontaneous
neutron neutron mass neutrons neutrons neutrons fission
fission fission /fission /fission /fission W/kg neutron/s/kg
barns barns kg years
The prompt kinetic energy released by fission is:
Fission energy (MeV)
Actinium 168
Thorium 172
Protactinium 177
Uranium 181
Neptunium 185
Plutonium 189
Americium 195
Curium 198
Berkelium 203
Californium 207
The neutron yield for a 1 GeV proton is:
Neutrons/Proton
Aluminum 2.2
Iron 4.1
Zirconium 6.3
Lead 11.9
Tantalum 12.7
Tungsten 13.1
Thorium 18
Uranium-238 21.4
Nucleus mass number = M = 184 Proton energy = E = 1 GeV Neutron yield = .10 * (A+20) (E-.12) = 18
Energy (GeV)
Secondary protons 212
Primary protons 194
Neutrons 26
Neutral pions 40
Charged pions 15
Heavy particles 15 More than one nucleon
Gammas 13
Muons 3.6
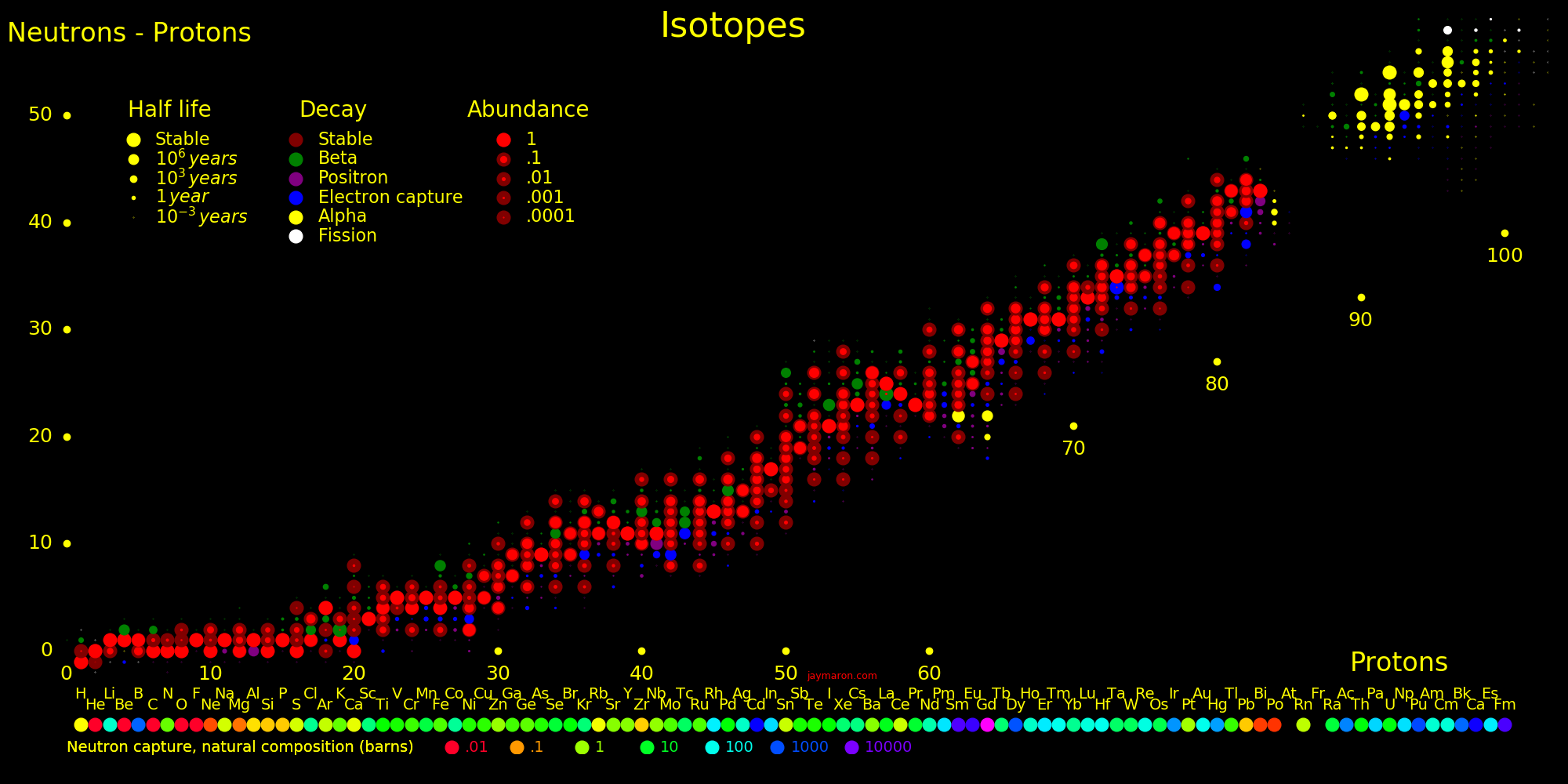 |
|---|
 |
|---|
The actinides are the elements from actinium to lawrencium. None are stable but many are long-lived.
 |
|---|
Neutron capture transmutes an isotope one space to the right and beta decay transmutes an isotope one space up.
The most massive nuclei that exist naturally are thorium-232, uranium-235, or uranium-238. All are unstable but have half lives larger than 700 million years. The road starts with these isotopes and then adding neutrons transmutes them according to the orange lines. The road forks at beta isotopes, which can either beta decay or capture a neutron.
The end of the road is fermium. Neutrons can't further increase the proton number because no fermium isotopes on the road beta decay. The road goes as far as fermium-258, which has a half life of .00037 seconds and spontaneously fissions. Producing heavier isotopes requires an accelerator or an extreme neutron flux (such as occurs in a fission bomb).
Most of the long-lived isotopes are on the neutron road, the most significant exceptions being neptunium-236 and berkelium-247. These isotopes can be reached by alpha decay, which moves an isotope 2 spaces down and 4 to the left.
Americium-242m (half live 141 years) is an excited state of Americium-242 (half life .0018 years) with a high thermal neutron capture cross section.
The thermal neutron capture cross section of Americium-241 to Americium-242 is 748 barns, and to Americium-242m is 83.8 barns.
 |
|---|
Transmutation rate is proportional to the neutron capture cross section. In order to move rightward on the road the isotope has to have a large neutron capture cross section and it has to have a large half life. This is true everywhere on the road except for curium-249, and so all the long-lived isotopes on the road are easily created, except for curium-250.
The road has a bottleneck at curium-246, which is the isotope with the lowest capture cross section (1.36 barns). The capture cross section of curium-248 is also low (2.49 barns). Traffic slows down here and all the isotopes further down the road have to wait for curium-246 and curium-248.
To create curium-250 you start with curium-248 and add a neutron to produce curium-249. Curium-249 has a half life of 64 minutes and you have to hope it captures a neutron before the decay.
 |
|---|
The fission cross section is for thermal neutrons with a Maxwellian spectrum centered at .025 eV. The isotopes with large fission cross sections are:
Thermal Critical Half life
neutron mass
fission
barns kg years
Americium-242m 6686 11 141
Californium-251 4801 5.5 900
Einsteinium-254 2900 9.9 .75
Neptunium-236 2800 6.8 154000
Curium-245 2161 10 8500
Californium-249 1665 6 351
Plutonium-241 937 12 14.3
Plutonium-239 748 10 24100
Curium-243 690 8 29.1
Uranium-235 538 52 704000000
Uranium-233 468 15 159200
 |
|---|
 |
|---|
 |
|---|
Fast Crit Crit Half life Fast Fast
neutron mass diam neutrons capture
fission /fission
barns kg cm years barns
Californium-252 2.32 2.73 4.30
Californium-251 1.28 5.46 900 4.56 .63r
Californium-249 1.74 6 351 *
Curium-247 1.86 7.0 *
Neptunium-236 7 154000 *
Curium-243 2.43 8 29.1 3.70 .4
Plutonium-238 1.994 9.5 3.148
Einsteinium-254 9.89 .75 *
Curium-245 1.75 10 8500 4.0 .4
Plutonium-239 1.800 10 24100 3.123
Americium-242m 1.83 10 141 3.53 .6
Plutonium-241 1.648 12 14.3 3.142
Curium-244 1.73 15 3.52 .8
Uranium-233 1.946 15 159200 2.649
Uranium-235 1.235 52 704000000 2.606
Plutonium-240 1.357 40 3.061
Curium-246 1.25 45 3.49 .4
Neptunium-237 1.335 60 2.889 1.8
Berkelium-247 75.7
Plutonium-242 1.127 80 3.07
Americium-241 1.378 60 3.457 2.0
Berkelium-249 192 3.74
Americium-243 .2i 200 3.45 1.8
Einsteinium-254m
Isotopes with a neutron capture cross section of 1 barn or more can be transmuted on a timescale of 10 years. Isotopes with a cross section smaller than this can't be practically transmuted.
To calculate the transmutation rate,
Neutron flux = F = 10-8 neutrons/barn/second Neutron capture = A = 10 barns Transmutation rate = R = FA = 10-7 transmutations/second = 3.2 transmutations/year
 |
 |
|---|---|
If a nucleus is hit with a pulse of neutrons then the probability that a fission occurs is:
Thermal neutron fission cross section = A = 6400 barns = 6.4⋅10-25 meters2 For Americium-242m Neutron pulse magnitude = F = 1020 neutrons/meter2 Fission probability = P = AF = 6.4⋅10-5 fissions
Actinides are useful for:
*) Neutron-induced fission
*) Radioactivity heat
*) Spontaneous fission
All of these properties are useful for spacecraft. The most useful actinides are:
Half life Neutron Spontaneous Radioactivity
fission fission
years barns Watts/kg Watts/kg
Uranium 233 159200 468
235 704000000 538
Plutonium 238 87.7 818
239 14100 748
241 14.3 937 4315
Americium 241 432
242m 141 6686
Curium 243 29.1 690 2666
244 18.1 4014
245 8500 2161
246 4730
247 15700000
248 340000 .64 .81
250 9000 240 241
Berkelium 249 .90
Californium 248 .91 86 86209 Off-road
249 351 1665
250 13.08 158 5778
251 900 4801
252 2.64 31227 58470
253 .049
254 .166 15896000 15897000
Einsteinium 254 .75 2900
Fermium 257 .275 ? 20000 279000
After Before
ppt ppt
U-234 .2
U-235 10.3 33
U-236 4.4
U-238 943 967
Pu-238 .18
Pu-239 5.7
Pu-240 2.21
Pu-241 1.19
Pu-242 .49
Np-237 .43
Am-241 .22
Am-242 .0007
Am-243 .10
Cm-242 .00013
Cm-243 .00032
Cm-244 .024
Fission products 35
Tc-99 .81
Neutron flux (Neutrons/cm2/second)
Power reactor 5e13
High-flux reactor 6e15
Cosmological s-process e16
Cosmological r-process e27
Fission bomb e31
Thermal Fast Crit Crit Half life Slow Fast SF Therm Fast Fast SF SF
neutron neutron mass diam neutr neut neut capt capt inel
fission fission /fiss /fiss /fiss barn barn W/kg neut/s/kg
barns barns kg cm years
Thorium-232 .078 2.16
Protactinium-231 .83 2.457
Uranium-232 80 2.013 3.296 2
Uranium-233 468 1.946 15 159200 2.48 2.649 73
Uranium-234 .407 1.223 2.578 1.8 3.9
Uranium-235 538 1.235 52 704000000 2.42 2.606 2.0 690 .0057
Uranium-236 .042 .594 2.526 1.8 2.3
Uranium-238 .00001 .308 2.601 1.97 2.68 5.51
Neptunium-236 2800 * 7 154000 * *
Neptunium-237 .019 1.335 60 2.54i 2.889 2 1.8 <.05
Neptunium-238 1243 1.45 .0058 2.79i 2.99i .1
Plutonium-237 2100i .124 * *
Plutonium-238 16.8 1.994 9.5 87.7 2.36 3.148 2.28 558 1204000 Alpha
Plutonium-239 748 1.800 10 24100 2.87 3.123 2.9 1017.3 10.1 Alpha
Plutonium-240 .030 1.357 40 6560 3.061 2.189 478000
Plutonium-241 937 1.648 12 14.3 2.92 3.142 36 <.8 Beta
Plutonium-242 .0026 1.127 80 373000 3.07 2.28 805000
Plutonium-243 181i
Plutonium-244 80800000
Plutonium-245 8500
Americium-241 3.1 1.378 60 3.12 3.457 2.0 500
Americium-242 1322i 3.4i .7
Americium-242m 6686 1.83 10 141 3.26 3.53i 2 .6
Americium-243 .2 .2i 200 3.20i 3.45i 1.8
Americium-244 1528i 3.4i * * .9
Americium-244m 1220i 3.4i 3.14i 3.42i .8
Curium-241 2600 2.21 .090
Curium-242 5 1.78 2.54
Curium-243 690 2.43 8 29.1 3.43 3.70i .4
Curium-244 1.1 1.73 15 18.1 2.72? 3.52i 16.2 .8 3.24i(t) Alpha
Curium-245 2161 1.75 10 8500 3.83 4.0 383 .4 Alpha
Curium-246 .17 1.25 45 2.93 3.49i .4 3.19i(t)
Curium-247 82 1.86 7.0 15700000 3.80 * 58 Alpha
Curium-248 .34 1.09 3.13 * .64
Curium-249 1.21
Curium-250 * .67 3.30 *
Berkelium-247 * 75.7
Berkelium-249 1.0 * 192 3.40 3.74i 240
Berkelium-250 959i
Californium-246 3.1
Californium-248 1.32 86
Californium-249 1665 1.74 6 351 4.06 * 3.4 481.4
Californium-250 112 1.49 3.51 * 158
Californium-251 4801 1.28 5.46 900 4.1 4.56 2839 .62 2.216 Alpha
Californium-252 33 2.32 2.73 2.64 4.00i 4.30i 3.75 20.4 31227 Alpha
Californium-253 1138 * * *
Californium-254 2.001j 1.80 .75 3.85 *
Einsteinium-253 2.51 * 4.7 * 15.9M
Einsteinium-254 2900 * 9.89 .75 4.2 *
Einsteinium-254m 1840 * * *
Fermium-244 4
Fermium-246 4
Fermium-254
Fermium-255 3360i * 4 *
Fermium-256 3.63 *
Fermium-257 * * .275 3.87 * 20000
Nobelium-252 4.2
Thermal Fast Critical Diam Half life Slow Fast SF SF Spontaneous
neutron neutron mass neutrons neutrons neutrons fission
fission fission /fission /fission /fission W/kg neutron/s/kg
barns barns kg years
The prompt kinetic energy released by fission is:
Fission energy (MeV)
Actinium 168
Thorium 172
Protactinium 177
Uranium 181
Neptunium 185
Plutonium 189
Americium 195
Curium 198
Berkelium 203
Californium 207
 |
|---|