





 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|
 |
|---|
 |
 |
|---|---|
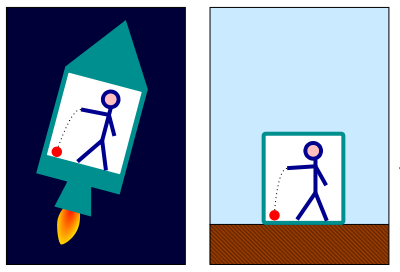
If you are stationary and observing a clock moving at speed V, the clock appears slow by a factor γ.
Velocity = V Speed of light = C Lorentz factor = γ = (1-V2/C2)1/2 Time measured on stationary clock = T Time measured on moving clock = t = T / γ
Time dilation is equivalent to length contraction. Neither occurs independently of the other.
Suppose a spaceship travels from the Earth to Mars and back at a speed of V =.8 C. Suppose also that the speed of light is 1 and that the distance from the Earth to Mars is 1.
Spaceship speed = V = 4/5 Speed of light = C = 1 Lorentz factor = γ = 5/3 Distance from Earth to Mars (Earth frame) = L = 1 Distance from Earth to Mars (ship frame) = l = 3/5 = V t = L / γ Travel time in the Earth frame = T = 5/4 = L/V Travel time in the ship frame = t = 3/4 = T/γ Time dilation: t = T/γ Length contraction: l = L/γThe Earth frame observes a slowdown of the spaceship clock, which is equivalent to the spaceship observing a shortening of the distance to Alpha Centauri.
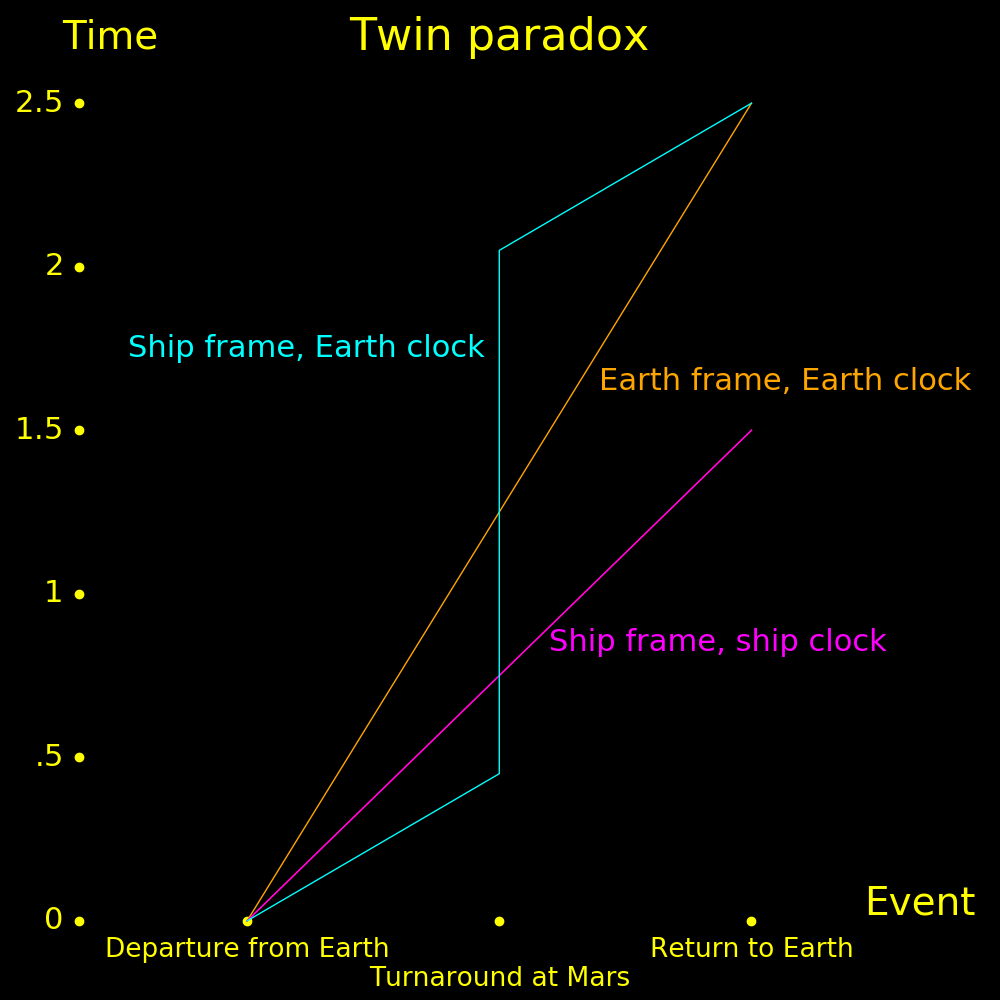
Suppose there are two twins, one that travels to Mars and back and the other that stays on the Earth. When the traveling twin returns he is younger than the stationary twin.
 |
|---|
Earth Earth Ship Ship
Timeline of Ship Ship frame, frame, frame, frame,
spaceship velocity position Earth Ship Earth Ship
clock clock clock clock
Before launch 0 0 .0 .0 .0 .0
Departs Earth +.8 0 .0 .0 .0 .0
Arrives at Mars +.8 1 1.25 .75 .45 .75
Stops at Mars 0 1 1.25 .75 1.25 .75
Departs Mars -.8 1 1.25 .75 2.05 .75
Arrives at Earth -.8 0 2.5 1.5 2.5 1.5
Stops at Earth 0 0 2.5 1.5 2.5 1.5
When the ship is moving, the Earth frame observes the ship clock to be slow and
the ship frame observes the Earth clock to be slow. Upon arrival at Mars, the
Earth observer sees his clock at T=1.25 and the ship clock as t=.75.
The ship observer sees his clock as t=.75 and the Earth clock as T=.45.
The time dilation factor for both observers is the same.
1.25 / .75 = 5/3 .75 / .45 = 5/3
Time depends on speed and location. As the ship turns around at Mars it observes the Earth clock to jump forward.
After the voyage the Earth clock and ship clock are at the same point in space and they are moving at the same speed (V=0). At this point the Earth clock reads 2.5 and the ship clock reads 1.5.
For a proper comparison of clocks, both clocks must be either:
*) At the same place but not necessarily at the same velocity.
or
*) At the same velocity but not necessarily at the same place.
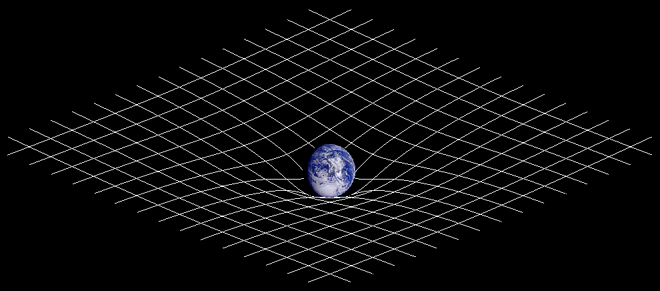
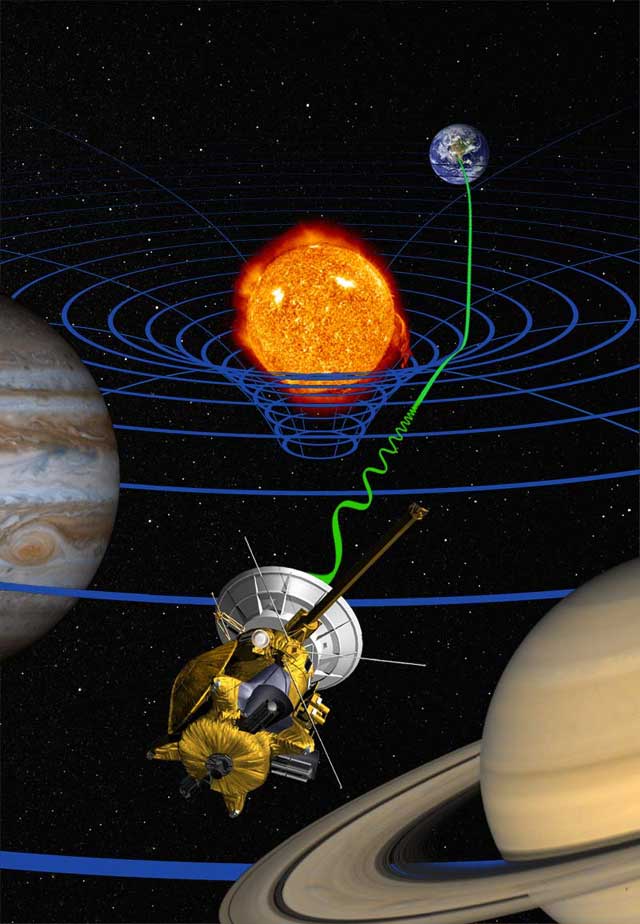
Special relativity covers objects that are moving at high speed in flat space (zero gravity). General relativity covers gravity. Both special relativity and general relativity contribute a time dilation and the total time dilation is the sum of both.
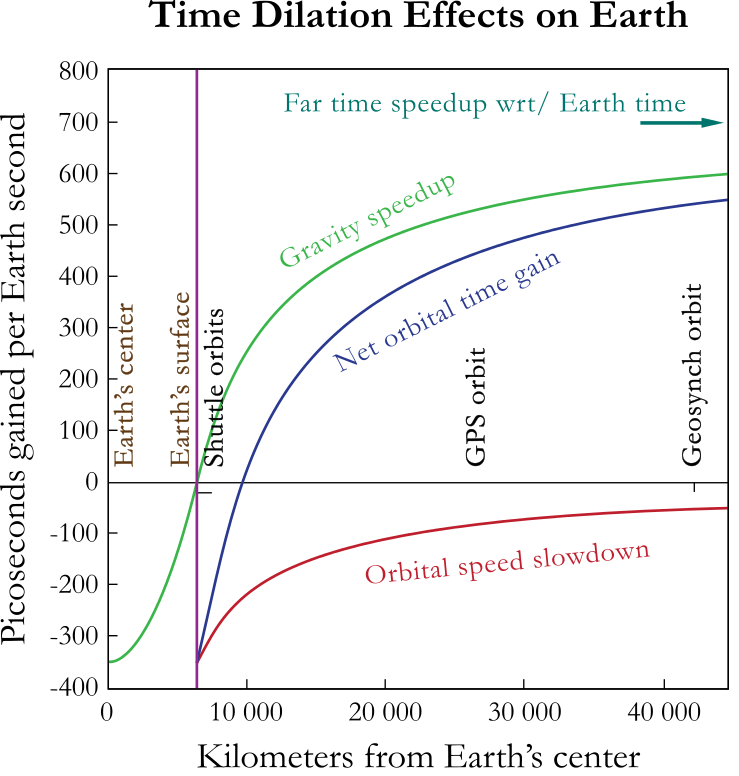
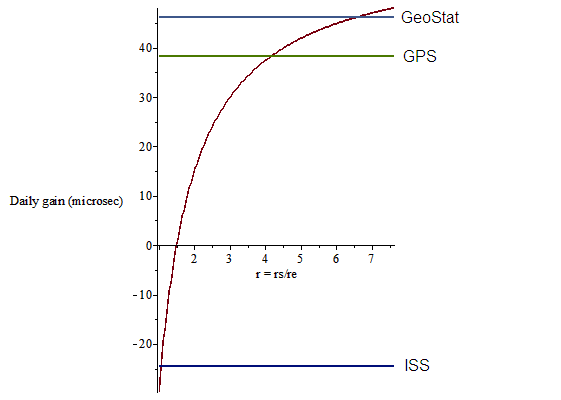
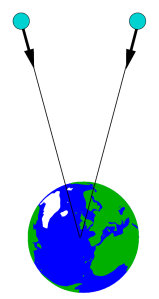
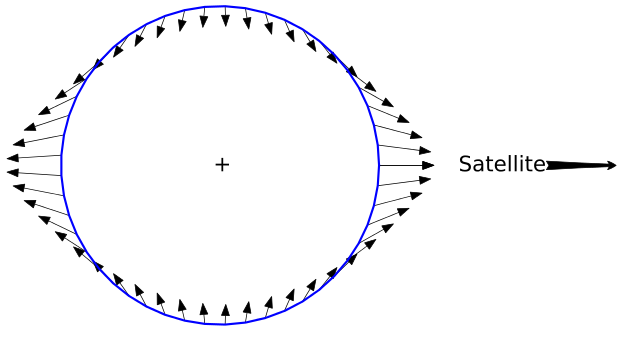
Suppose there is a stationary observer on the Earth and an observer in orbit at 500 km and moving at 8 km/s. The stationary observer find that the orbiting clock is slower due to its speed (special relativity) and faster due to being at a higher gravitational potential (general relativity). The two effects add accoring to the figures below.
 |
 |
|---|---|
 |
|---|
General relativity is built from the equivalence principle:
An oberver in an accelerating rocket and zero gravity experiences the same laws of physics as a stationary observer in Earth gravity.
The gravitational redshift of photons can be derived using the equivalence principle.
 |
|---|
If a photon travels upward by a height H it loses energy to gravity.
h = Planck constant = 6.62e-34 Joule seconds F = Frequency of a photon emitted at height zero f = Frequency of a photon received at height H E = Energy of the photon when it is emitted = h F H = Height that the photon gains between being emitted and received g = Gravitational acceleration C = Speed of lightWe assume that the relative change in frequency is small
F-f << FChange in photon energy = Change in gravitational energy
h (F - f) = g H E/C2
F-f = g H E / (h C2)
= g H F / C2
The fractional change in frequency (redshift) is
(F-f) / F = g H / C2The redshift can equivalently be interpreted as a slowdown of time at height 0 compared to height H. The farther down you are in a gravitational potential the slower time passes. This is "gravitational time dilation". The fractional change in the clock rate is g H / C2.
dF = Change in frequency of the photon
= F-f
dF/F = Fractional change in frequency
T = Time for one oscillation of a photon at height 0
t = Time for one oscillation of a photon at height H
dT = Change in period
= T-t
dT/T = Fractional change in period
F = 1/T
dT/T = -dF/F
= -g H / C2
We can use the above result to derive the gravitational time dilation at any distance from a point mass. This is the "Schwarzschild metric" and contains an event horizon.
G = Gravity constant
= 6.67e-11 Newton meters2/kg2
M = Mass of the point mass
R = Distance from the point mass
g = Gravitational acceleration
= - G M / R2
T = Time dilation factor as a function of R
dT/T = - g H / C2
= (G M / R2) * dR / C2
dT / T = (G M / C2) dR / R2
ln(T) = (G M / C2) / R
 |
|---|
Objects in a gravitational well experience time more slowly than objects in flat space.
M = Mass of gravitating object G = Gravity constant R = Distance from the gravitating object g = Gravitational acceleration = G M / R2 C = Speed of light Rs = Schwarzschild radius for the gravitating object = Radius of the event horizon = 2 G M / C2 T = Time for one oscillation of a photon as a function of R t = Time for one oscillation of a photon at R = Infinity dR = Change in distance from the gravitating object = H (The height from the above calculation)The time dilation factor is
T = t = tIf the photon is far from the gravitating object and if the change is R is small then this formula reduces to the approximation given above.
T = t
~ t (1 + G M / (R C2))
dT ~ G M t dR / (R2 C2)
dT/T = G M dR / (R2 C2) For small redshifts we approximate T~t so that dT/T ~ dT/t.
= g H dR / C2
= g H / C2
If you are far from a black hole but not at infinity then the time delay factor is
d = 1 - (1-Rs/R)½ ~ .5 Rs / R
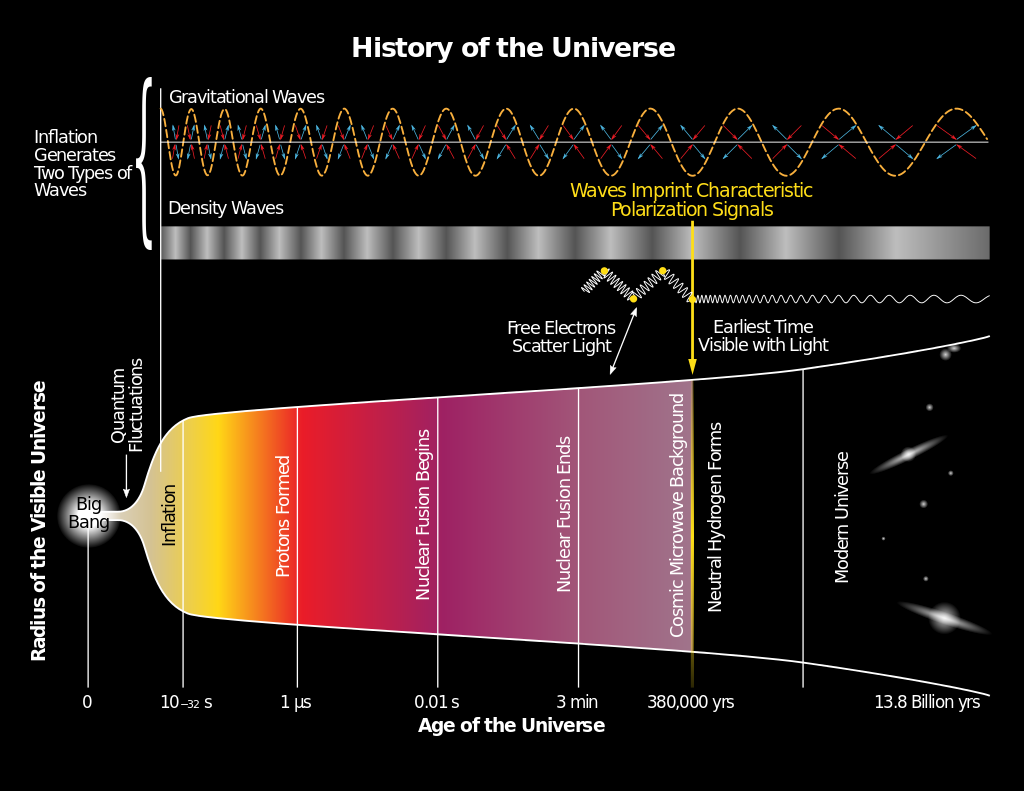
1859 Mercury's orbit is found to deviate from Newtonian gravity
1905 Theory of special relativity developed
1915 Theory of general relativity developed
1915 Schwarzschild solves the metric for a point mass and find that
general relativity implies an event horizon (black hole)
1919 Eddington measures the deflection of starlight during a solar eclipse
and confirms the prediction of general relativity
1922 Friedmann finds a solution in which the universe may expand or contract.
Einstein adds a cosmological constant to general relativity.
1927 Lemaitre showed that static solutions of the Einstein equations,
which are possible in the presence of the cosmological constant,
are unstable, and therefore the static universe envisioned by Einstein
could not exist (it must either expand or contract)
1929 Hubble finds that the universe is expanding
1963 Kerr solves the metric for a spinning black hole
1966 Shapiro measures the gravitational time delay of photons
1974 Hulse and Taylor analyze a double pulsar and confirm that it emits
gravitational waves consistent with general relativity
1958 Mossbauer effect discovered, allowing for high-precision measurements of
photon energy
1959 Pound and Rebka use the Mossbauer effect to measure the gravitational redshift
2007 The Gravity Probe B satellite detects frame-dragging and the geodetic effect
In the film "Interstellar" the astronauts experience extreme gravitational time dilation. This is likely accompanied by extreme tidal forces.
If we assume that the source of warping of space is a black hole then
G = Gravitational constant M = Mass of the black hole C = Speed of light Rs = Radius of the event horizon of a black hole (Schwarzschild radius) = 2 G M / C2 D = Gravitational time dilation factor = = 1 for R -> Infinity = 0 at the black hole event horizon A = Gravitational acceleration = - G M / R2 Z = Gradient of the acceleration = dA/dR = - 2 G M / R3 = - Rs C^2 / R3Suppose we consider D=.5 to be onset of extreme time dilation. D=.5 corresponds to R = (4/3) Rs. In other words you need to be quite close to the black hole. The time dilation experienced in the film was even more extreme than this.
Suppose we consider Z=1 to be the largest tidal force that can be endured over a sustained period of time. If
Z=1 at R = (4/3) Rsthen the mass of the black hole is
Z = (27/256) C6 / (G M)2 M = (27/256)½ C3 / G / Z½ ~ .3 C3 / G / Z½ ~ 1.2e35 kg ~ 60000 solar massesTo experience extreme time dilation while not getting spaghettified you need a large black hole.
 |
 |
|---|---|
General relativity bends light by twice the amount predicted by Newtonian mechanics.
 |
 |
|---|---|
 |
|---|
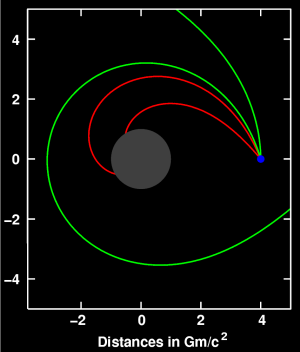
In Newtonian gravity, if 2 gravitatating objects are ideal point masses then the orbits don't precesss, and in general relativity they do. In 1859 Mercury's orbit was found to precess, and the precession was found to be in accord with general relativity.
 |
|---|
A photon launched tangental to a black hole will orbit as a circle if it is at 3/2 times the event horizon radius. If it is closer it will spiral in and if it is further it will escape.
The circular orbit is unstable. If the photon deviates from the circle it will either fall into the hole or escape.
 |
|---|
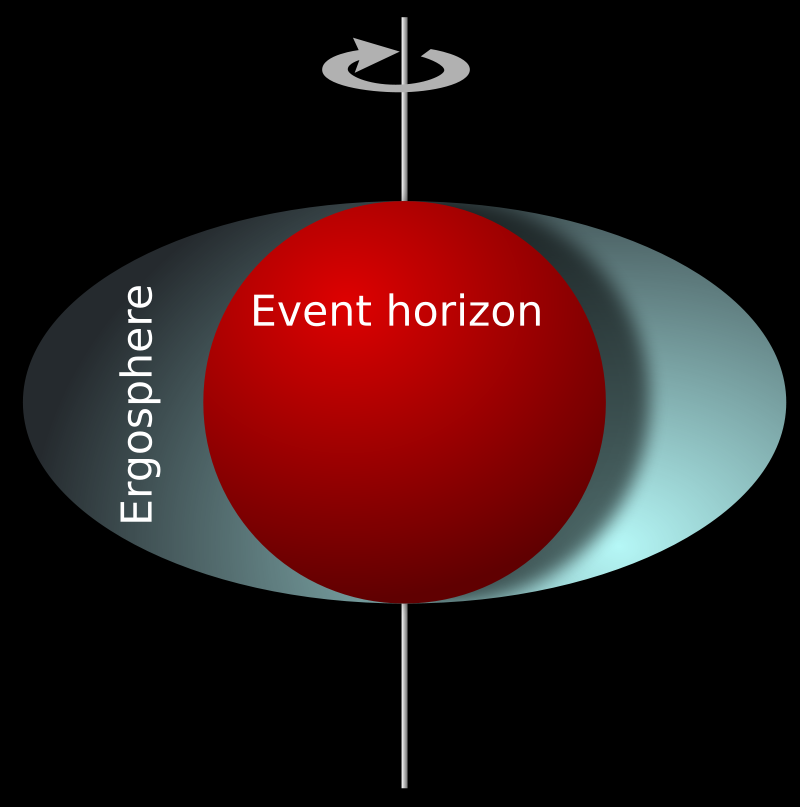
A spinning black hole drags the space around it. Photons orbiting the hole in the direction of the spin appear to move faster than photons orbiting counter to the spin.
 |
 |
 |
|---|---|---|
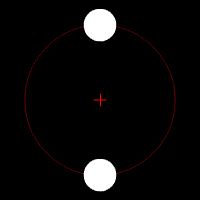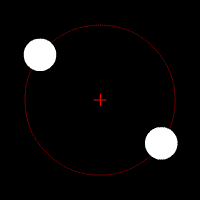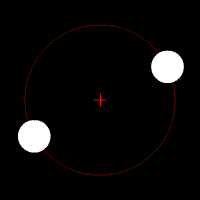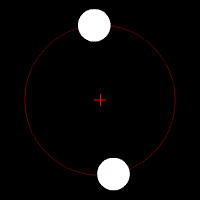
Objects near a black hole experience extreme tidal forces.
 |
 |
 |
|---|---|---|
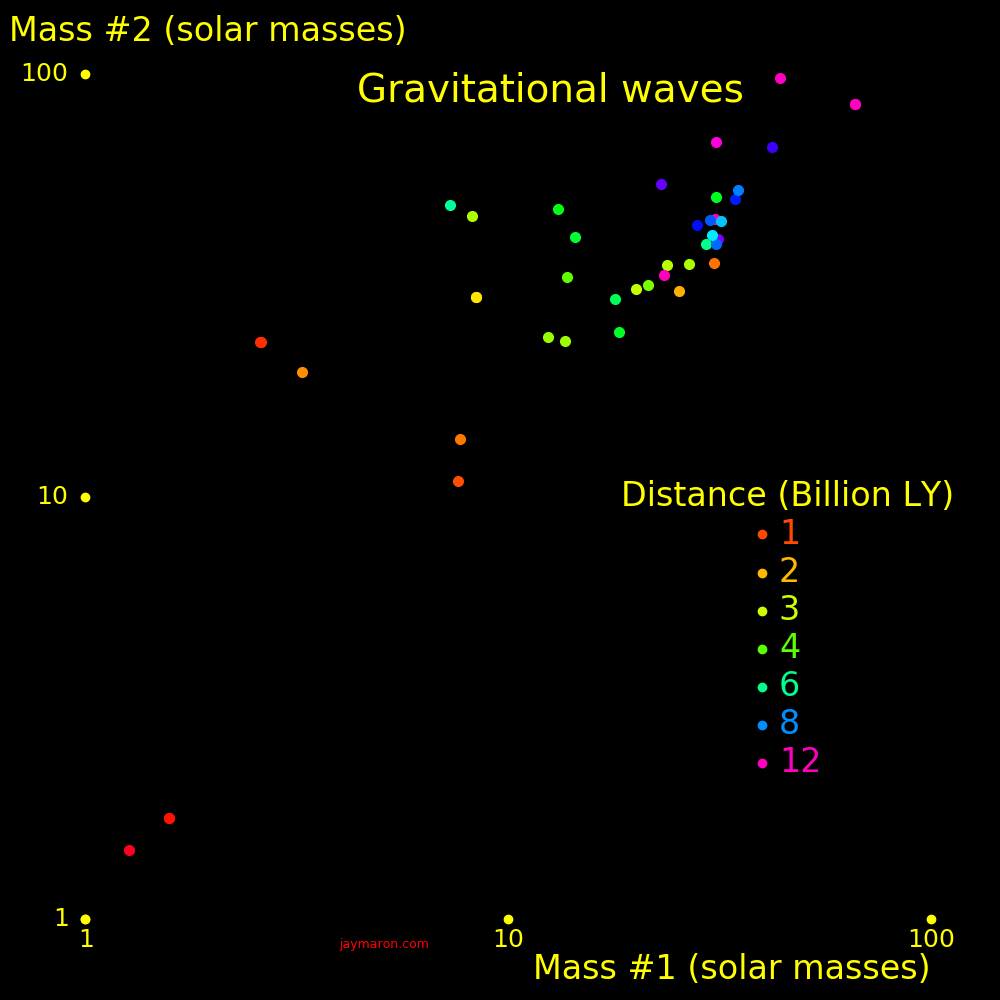
Two orbiting objects emit gravitational waves. If the objects are large enough the will lose energy, inspiral, and merge.
 |
|---|
 |
|---|
 |
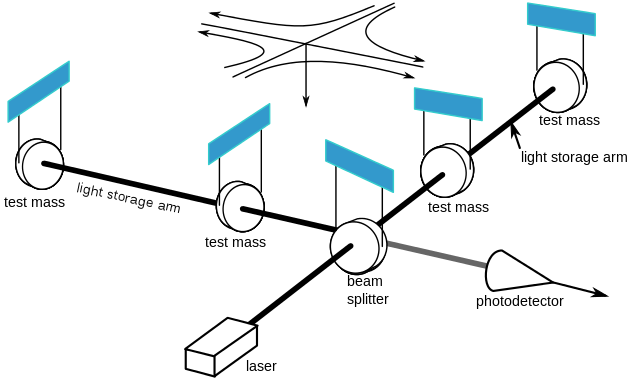 |
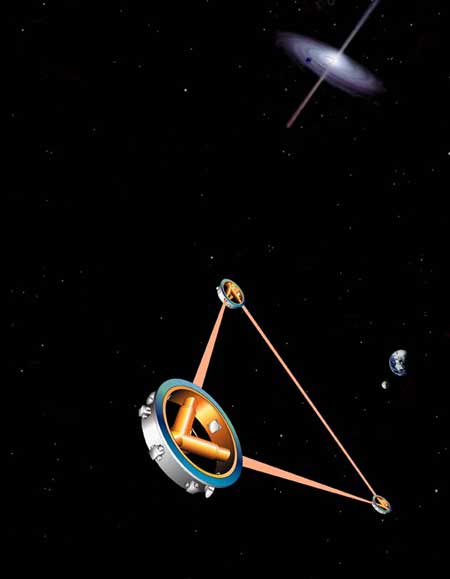 |
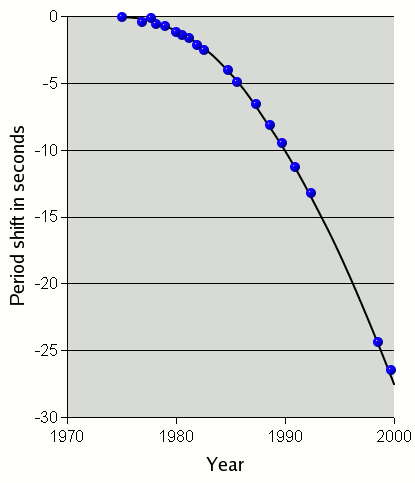 |
|---|---|---|---|
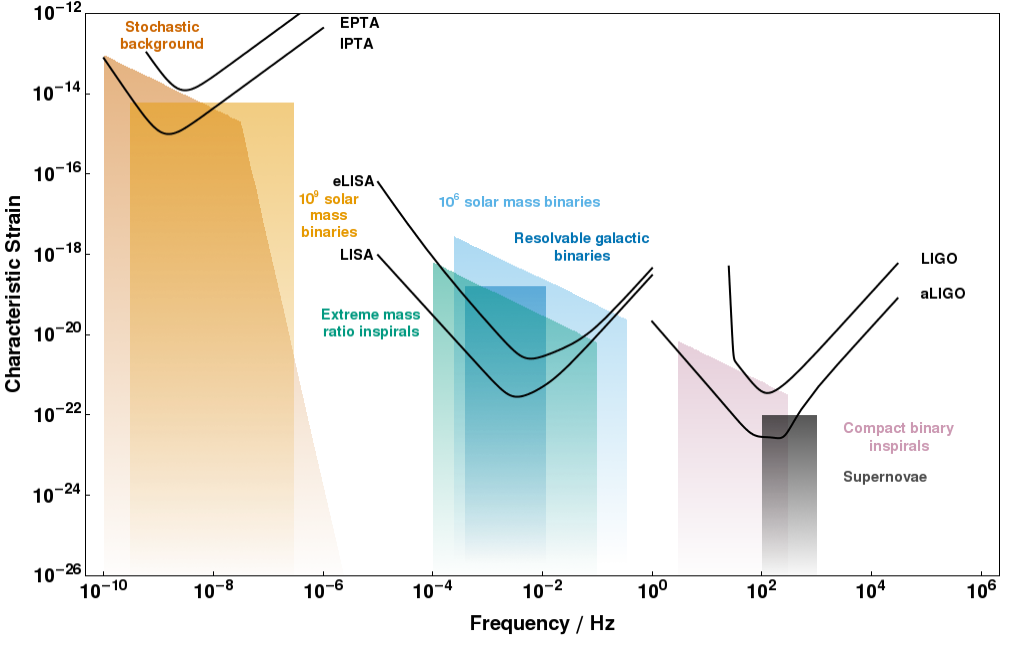 |
|---|
 |
 |
 |
|---|---|---|
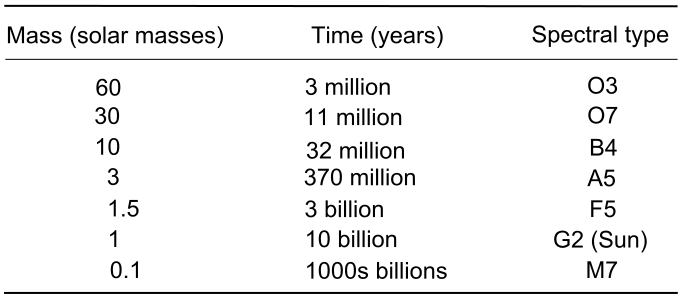
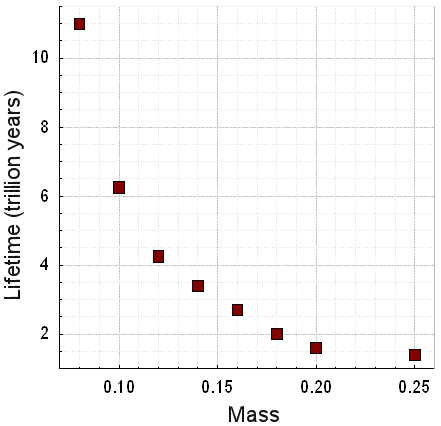
Sirius B and Pegasi B are white dwarfs and they appear as the small blue dots in the images.
 |
 |
|---|---|
 |
 |
|---|---|
 |
|---|
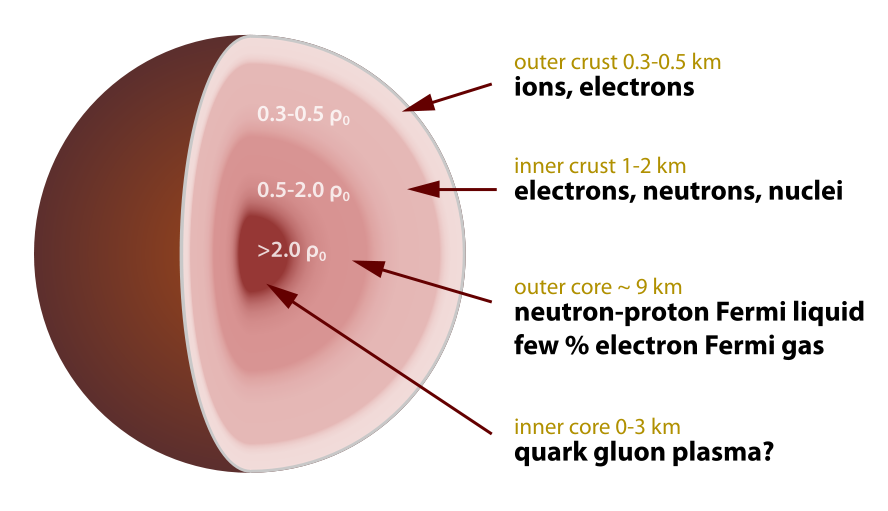
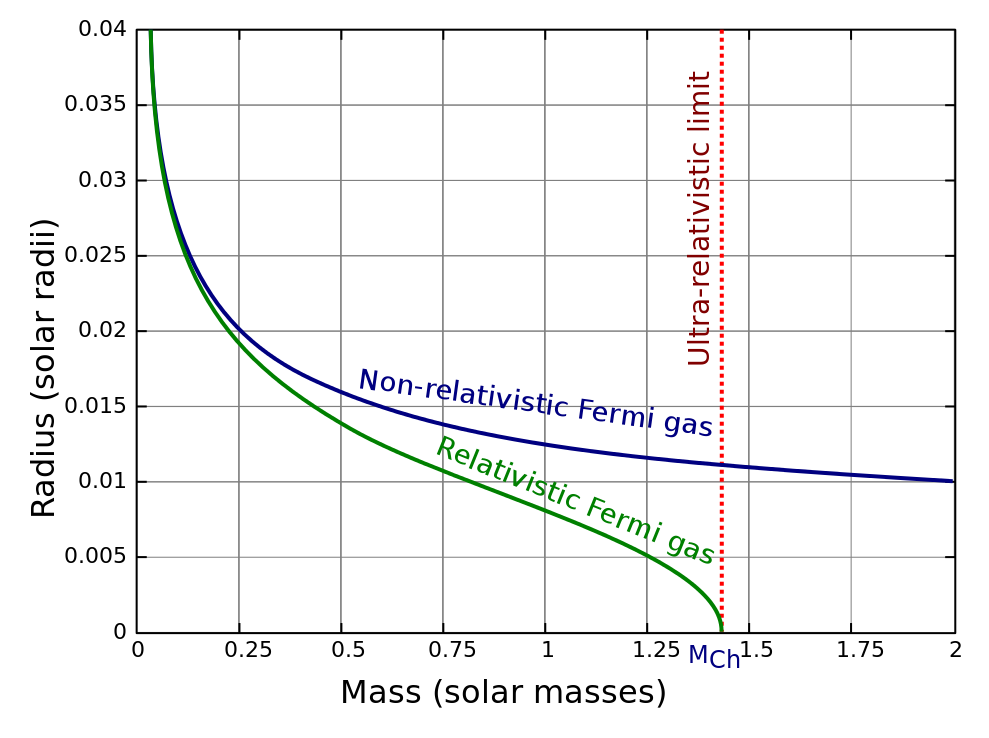
M = Star mass in solar masses Case Death Remnant M < 9 Red giant White dwarf 9 < M < 20 Supernova Neutron star M > 20 Supernova Black hole
After a star runs out of fusion fuel the core contracts. Electron pressure can hold up the core unless the mass exceeds 1.4 solar masses (the Chandrasekhar limit), at which point electrons combine with protons to produce neutrons and the core collapses into a neutron star. The energy released powers a supernova and ejects the surface layer.
Neutron pressure can hold up a neutron star unless the mass exceeds 3 solar masses, at which point it collapses into a black hole.
Object Mass Radius Core Core
(Sun=1) (km) density state
(g/cm3)
Earth .000003 6371 12 Iron
Jupiter .00096 69900 25 Iron
Red dwarf .08 70000 100 Plasma
Sun 1 696000 150 Plasma
White dwarf max 1.4 3500 1e8 Electron matter
Neutron star max 3 13 8e14 Neutron matter
Black hole min 3 9 2e15 The radius refers to the event horizon radius
Density (g/cm3)
Water 1.0
Iron 7.9
Osmium 22.6 Densest element
Earth core 12
White dwarf max 1e8
Nuclear matter 2e14
Neutron star max 8e14 Maximum core density before collapsing into a black hole
Black hole 2e15 Density of a 3 solar mass black hole (mean density inside the event horizon)
 |
 |
|---|---|
All neutron stars have extreme magnetic fields, and the ones with the most extreme fields are called magnetars. Magnetars have a field of between 108 and 1011 Tesla. A neodymium magnet has a field of 1.25 tesla and a magnetic energy density of 4.0e5 J/m3. A magnetar's 1010 tesla field, by contrast, has an energy density of 4.0e25 J/m3. The magnetic field of a magnetar is lethal at a distance of 1000 km due to the strong magnetic field distorting the electron clouds of the subject's constituent atoms, rendering the chemistry of life impossible. At a distance halfway to the moon, a magnetar could strip information from the magnetic stripes of all credit cards on Earth. As of 2010, they are the most magnetic objects ever detected in the universe.
As described in the February 2003 Scientific American cover story, remarkable things happen within a magnetic field of magnetar strength. "X-ray photons readily split in two or merge together. The vacuum itself is polarized, becoming strongly birefringent, like a calcite crystal. Atoms are deformed into long cylinders thinner than the quantum-relativistic de Broglie wavelength of an electron." In a field of about 105 teslas atomic orbitals deform into rod shapes. At 1010 teslas a hydrogen atom becomes a spindle 200 times narrower than its normal diameter.
Magnetic field in Teslas
Field generated by brain 10-12
Wire carrying 1 Amp .00002 1 cm from the wire
Earth magnetic field .0000305 at the equator
Neodymium magnet 1.4
Magnetic resonance imaging machine 8
Large Hadron Collider magnets 8.3
Field for frog levitation 16
Strongest electromagnet 32.2 without using superconductors
Strongest electromagnet 45 using superconductors
Neutron star 1010
Magnetar neutron star 1014
Mass Radius Schwarzschild Surface grav Surface tide Escape Core Core temp
(Sun=1) (km) radius (km) (m/s2) (m/s2/m) speed density (MKelvin)
(C=1) (g/cm3)
Sun 1 696000 3.0 279.4 .00000039 .0021 150 15
Red dwarf .08 70000 .24 2170 .00000031 .0018 100 13
Jupiter .00096 69900 .0028 24.8 .00000037 .00020 25 .036
Earth .000003 6371 .000009 9.8 .0000015 .000037 12 .006
White dwarf max 1.4 3500 4 15000000 4.3 .034 e8 10
Neutron star max 3 13 9 2.4e12 180000000 .82 8e14 1
Black hole min 3 9 9 4.9e13 550000000 1 2e15 -
Milky Way BH 4200000 - 12400000 3600000 .00029 1 1050 -
Andromeda BH 200000000 - 5.9e8 76000 .00000013 1 .46 -
APM-08279 BH 23000000000 - 6.8e10 660 9.7e-12 1 .00003 -
Gravity constant = 6.67e-11 N m2 / kg2
Sun mass = 1.989e30 kg
Schwarzschild radius = 2 G M / C2
Sun Schwarzschild radius = 2.95 km
Iron nucleus density = 2.3e14 g/cm3
Neutron star core pressure= 1.6e35 Pascals
The tidal magnitude is the change in gravitational acceleration per distance from the
gravitating object.
Tidal magnitude Effect on a human
(m/s2/m)
.1 Minimum perceptible
1 Tangibly perceptible
10 Uncomfortable
50 Threshold for blackout, where the heart cannot pump blood to the brain
If you are standing on the surface of a white dwarf then the tidal magnitude is
tangible but not uncomfortable. The gravity, however, is enough to squash you.
The larger the mass of a black hole, the smaller the tidal magnitude at the Schwarzschild radius. The tidal magnitude is imperceptible at the surface of the Milky Way supermassive black hole.
The largest known black hole is AMP-08279.
For the above calculations we have assumed Newtonian physics, which is okay if the escape speed is substantially less than the speed of light. This applies for stars, planets, and white dwarfs, but not for neutron stars and black holes. For these objects you need general relativity and the Newtonian numbers should be regarded as approximate.
 |
|---|
Matter falling into a black hole forms an accretion disk. The disk generates a magnetic field and the field ejects material from the disk in a jet. Most of the material falls into the hole and some is ejected in the jet.
Photon frequency = F Photon wavelength = W Photon speed = C = 3.00⋅108 meter/second Planck constant = h = 6.62⋅10-34 Joule second Photon momentum = Q Photon energy = E Wave equation C = FW Energy equation E = hF Momentum equation E = QC de Brogie equation h = QW
Photons have zero rest mass. In 1924 de Broglie found that the equation h=QW also applies to particles with finite rest mass. W is the quantum-mechanical wavelength of a particle.
For particles with positive rest mass, we add the following variables.
Speed = V Lorentz gamma = γ = (1-V2/C2)-½ Rest mass = m Relativistic mass = M = γ m
The following equations apply for all particles, whether the rest mass is zero or positive.
Q W = h de Broglie equation E = (mC2)2 + (QC)2
If the particle has zero rest mass (m=0), such as a photon, the equation reduces to:
E = Q C
A photon has an effective relativistic mass of
E = M C2
If the particle has positive rest mass then
E = M C2 Q = M VIn many cases you can transform a classical formula to a relativistic formula by replacing "m" with "M", such as above.
If you try to accelerate a particle to the speed of light,
V/C → 1 M → ∞ Acceleration → 0The particle never reaches the speed of light.
 |
|---|
We can define 4 regimes.
Classical V/C << 1 Relativistic V/C not close to zero and not close to 1 Ultrarelativistic V/C close to 1 but not equal to 1 Photon V/C = 1
The classical regime is a simplification of the relativistic equations.
The ultrarelativistic regime can often be approximated with the photon regime.
If the simplified regimes are not sufficiently precise then you have to use the full relativistic equations.
V/C → 0 M → m γ → 1 + ½ V2/C2 E → E = m C2 + ½ m V2 A rest energy plus a kinetic energy Q → m V
For particles with zero rest mass, such as photons,
E = Q C
E → Q C
In a stationary frame, let an event have space and time coordinates
S = (X,T)In a frame moving at speed +V, the event has coordinates
s = (x,t)In classical physics, s is related to S by
x = X - V T t = TThis is "Galilean relativity". In this transform, t doesn't depend on X. Time is absolute.
In special relativity,
C = Speed of light in the stationary frame c = Speed of light in the moving frame Z = 1 / Squareroot(1-V2/C2) x = Z (X - VT) t = Z (T - VX/C2)This is the "Lorentz transform".
The time transform depends both on time and space. Time is not absolute.
If V << C, Z = (1-V2/C2)-½ ~ 1 + .5 V2/C2If you are on an airplane moving at the speed of sound, V = 300 m/s and
Z ~ 1 + 5e-13The effects of realativity are hard to notice at this speed.
Suppose a photon is created in the stationary frame at S=(0,0) and travels to the right at speed C. Its coordinates in the stationary frame are
X = C TIn Galilean relativity, the coordinate of the photon in the moving frame is
t = T x = X - V T = CT - VT = (C-V) tIn the moving frame the photon moves to the right at speed (C-V).
In special relativity, the coordinate of the photon in the moving frame is
x = Z (X - VT) = Z (CT - VT ) = Z T (1-V/C) C t = Z (T - VX/C2) = Z (T - VT/C) = Z T (1-V/C)The speed of the photon in the moving frame is
c = x/t = CThe photon moves at speed C in the moving frame. The Lorentz transform preserves the speed of light.
The Lorentz transform gives the coordinates in the moving frame as a function of the coordinates in the stationary frame. In other words,
(x,t) as a function of (X,T).We can invert the transform to express the coordinates in the stationary frame as a function of the coordinates in the moving frame. In other words,
(X,T) as a function of (x,t)The inverse transform can be obtained by replacing +V with -V in the forward transform.
Lorentz transform: Inverse transform: x = Z (X - V T) X = Z (x + V t) t = Z (T - V X / C2) T = Z (t + V x / C2)
Suppose a moving spaceship fires a cannon. What is the speed of the cannonball in the stationary frame?
V = Spaceship velocity with respect to the stationary frame
v = Cannonball velocity with respect to the spaceship
U = Velocity of the cannonball in the stationary frame
(V + v) / (1 + Vv/C2) Velocity addition formula
In Galilean relativity,
U = V + vThe cannonball is fired at (X,T) = (x,t) = (0,0). The coordinates of the cannonball in the spaceship frame are x = vt. In the stationary frame, the projectile is at
X = Z (x + Vt) = Z (vt + Vt) T = Z (t + Vx/C2) = Z (t + Vvt/C2) U = X/T = (V + v) / (1 + Vv/C2) If v < C, then U < C If v = C, then U = C (if the cannonball is replaced by a photon)If an object moves at less than the speed of light in one frame, then it moves less than the speed of light in all frames.
If an object moves at the speed of light in one frame, it moves at the speed of light in all frames.
Suppose you see two simultaneous flashes of light.
(Space,time)
Flash #1 = S1 = (X1,T1)
Flash #2 = S2 = (X2,T2)
The "invariant interval" between S1 and S2 is
S = (X2-X1)2 - C2 (T2-T1)2Shift the coordinate system so that X1=T1=0
(Space,time)
Flash #1 = S1 = (0,0)
Flash #2 = S2 = (X,T)
In the moving frame,
(Space,time)
Flash #1 = s1 = (0,0)
Flash #2 = s2 = (x,t)
S = X2 - C2 T2
s = x2 - C2 t2
The Lorentz transform preserves the invariant interval.
S2 = s2If a photon is created in the first flash and arrives at the instant of the second flash,
S2 = s2 = 0The path of a photon from one place to another always has an invariant interval equal to 0. This is equivalent to saying that the speed of light is constant in all frames.
Suppose that it's possible to travel from Flash #1 to Flash #2 at speed V, where V < C. Then
S2 > 0 and s2 > 0If S2 > 0, we say that the two flashes are "causally connected" and that the interval is a "timelike interval". It is possible for Flash #1 to have an effect on Flash #2.
If two flashes are causally connected in one frame then they are causally connected in all frames.
Suppose it's not possible to travel from Flash #1 to Flash #2, even if you are moving at the speed of light. Then
S2 < 0 and s2 < 0We say that the two flashes are "causally disconnected" and that the interval is a "spacelike interval". It is not possible for Flash #1 to have an effect on Flash #2.
If two flashes are causally disconnected in one frame then they causally disconnected in all frames.
The Lorentz transform preserves causality.
If two flashes are causally connected then there exists a frame where they occur at the same point in space. The time between the flashes in this frame is the "Proper time". The observed time between flashes is longer in all other frames (time dilation).
Let the coordinates of two flashes in the stationary frame be
Flash #1 = S1 = (0,0) Flash #2 = S2 = (0,T)In a moving frame,
Flash #1 = s1 = (0,0) Flash #2 = s2 = (x,t)The proper time is T. We use the forward Lorentz transform to obtain the position and time for flash #2 as observed in the moving frame.
t = Z (T - V 0 / C2) = Z T t > T (time dilation)The time measured between two events is smallest in the frame where the events occur at the same place (the proper time).
V = Velocity of the ships
C = Speed of light
d = Distance between the ships, which is the same in both the ship and
stationary frames
= Distance the light beam travels as it goes from the top ship to the bottom ship,
in the ship frame
D = Distance the light beam travels as it goes from the top ship to the bottom ship,
in the stationary frame
t = Time required for the light signal to travel from the top ship to the bottom ship
in the ship frame
= d / C
T = Time required for the light signal to travel from the top ship to the bottom ship
in the stationary frame
= D / C
L = Distance the ships move as the light signal travels from the top ship to the
bottom ship, in the stationary frame.
= V T
= V D / C
Q = Lorentz time dilation factor
= (1-V2/C2)-½
D can be evaluated by constructing a right triangle.
D2 = d2 + L2
= d2 + V2 D2 / C2
D2 (1-V2/C2) = d2
D = Q d
T = Q t
More time passes in the stationary frame than in the ship frame by a factor of Q.
1800 Volta invents the battery, enabling the generation of large electric currents
1803 Young discovers the diffraction of light, suggesting that light is a wave
1820 Orsted finds that an electric current produces a magnetic field
1820 Ampere finds that electric currents attract each other
1831 Faraday finds that a changing magnetic field produces an electric field
1861 Maxwell finds that a changing electric field produces a magnetic field
1861 Maxwell develops the "Maxwell's equations", unifying electricity and magnetism
1864 Maxwell finds that light is an electromagnetic wave
This theory contained a paradox, that the speed of light is invariant
1884 Heaviside invents the vector calculus and uses it to simplify Maxwell's equations
1887 Hertz achieves the first detection of electromagnetic waves
1887 Michelson-Morley experiment finds that the speed of light is invariant
1889 Heaviside publishes the force law for a charge moving in a magnetic field
1892 Lorentz discovers the "Lorentz transform" for special relativity
This offered an explanation for the Michelson-Morley experiment
1904 Lorentz finds that the "Lorentz transform" resolves the paradoxes of
Maxwell's equations
1905 Einstein and Poincare each publish a complete formulation of the theory
of special relativity
1915 Einstein develops the theory of general relativity
V = Velocity of spaceship v = Velocity of cannonball fired from the ship, in the ship frame U = Velocity of the cannonball in the rest frame C = Speed of light U = (V + v) / (1 - Vv/C2)This equation forbids anything from reaching the speed of light.
If V < C and v < C then U < C.If the cannonball is a photon,
v = C U = CThe speed of light is the same in both the ship and the stationary frame
Suppose a multistage rocket is such that: The first stage accelerates from rest to .5 C. The second stage accelerates from rest to .5 C, in the frame of the first stage. Etc.
If the rocket has 5 stages, what is the velocity of each stage in the rest frame? What is the Lorentz factor of the final stage?
The magnetic force is inconsistent with Galilean relativity because it depends on the speed of the charge. Special relativity resolves the inconsistency.
Suppose two equal charges are moving in parallel. In CGS units,
Electric charge = Q
Distance between the charges = R
Velocity of the charges = V
Speed of light = C
Mass of the charges = M
Lorentz gamma factor = Z = (1-V2/C2)-½
Electric force in the moving frame = Fe = Q2 R-2
Electric accel. in the moving frame = Amove= F/M = Q2 R-2 M-1
Electric accel. in the rest frame = Arest= Amove Z-2 = Q2 R-2 (1-V/C2) M-1
Electric force in the rest rame = Q2 R-2 - Q2 (V/C)2 R-2
= Fe + Fm
Magnetic force between the charges = Fm = -Q2 (V/C)2 R-2
Two stationary charges experience an electric repulsion. If the charges move in parallel, time dilation slows down the electric force, which can be interpreted as an added attractive force. This attractive force is the magnetic force.
 |
|---|
 |
|---|