





 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|
 |
|---|
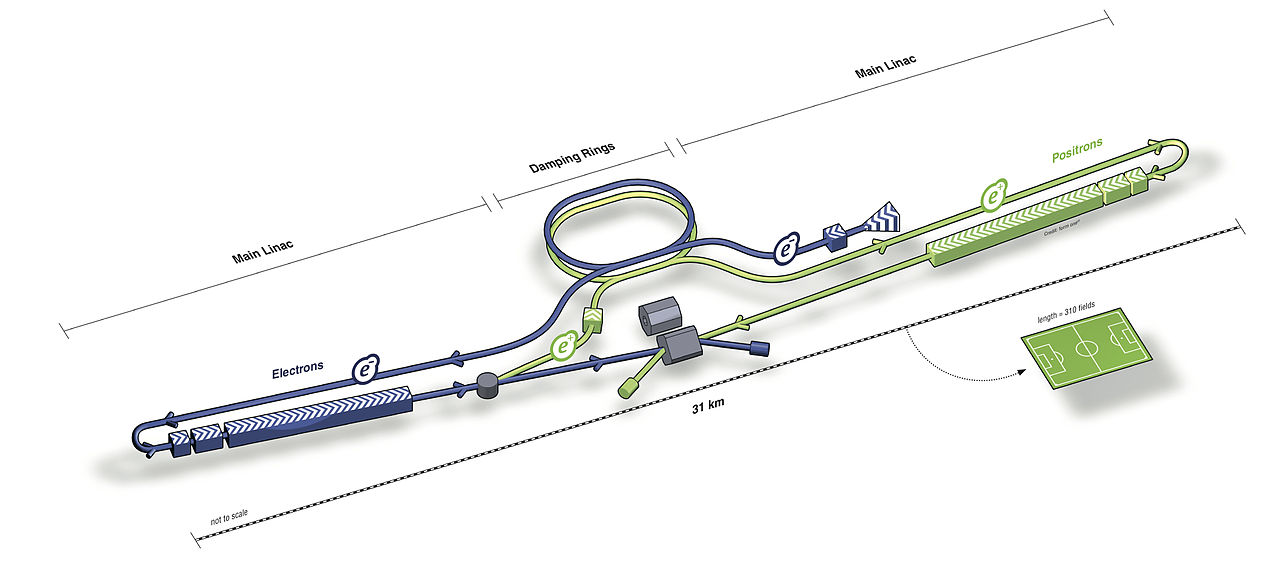
Particle physics is starved for data. The Large Hadron Collider discovered all particles it's capable of discovering and now we need a bigger collider. The options are a linear electron collider and a ring proton collider.
 |
 |
|---|---|
In a proton ring collider, a set of protons circles clockwise and another set circles counterclockwise, and they're arranged to collide.
In a linear electron collider, electrons start at one end and positrons start at the other end, and both are accelerated toward the center and arranged to collide.
Linear and ring colliders have contrasting strengths and weaknesses.
A ring proton collider can reach a higher energy than a linear electron collider.
Electron-positron collisions give more precise data than proton-proton collisions.
An electron ring collider has a maximum energy of .25 TeV, above which electrons lose energy to synchrotron radiation. This is why a high-energy electron collider has to be linear. Proton ring colliders don't have the synchrotron problem and can be arbitrarily large.
A linear electron collider that is longer than 100 km has to follow the Earth's curvature, giving it a maximum energy of 23 TeV. Above this energy, electrons lose energy to synchrotron radiaton.
In an electron-positron collision, if the electron energy is X, then the maximum energy of a particle that the collision can create is X. For proton-proton collisions, the maximum energy of a created particle is less, on the order of .15 X.
A linear collider can be built incrementally. You can always increase the length. A ring collider can't be made larger. However, you can use an existing ring collider as an injector for a bigger collider. A hypothetical strategy is to build a .25 TeV electron linear collider to study the top quark and Higgs boson, and then extend it beyond 1 TeV.
An electron linear collider is under consideration by CERN, to reside in Switzerland and France.
A proton ring collider is under consideration by China. The tunnel that hosts the proton collider will also host an electron ring collider at .2 TeV, for mass production of top quarks and Higgs bosons, to refine their measurements.
Type Particle Energy Size Year Particles discovered
GeV km
Stanford Linear Collider Linear Electron 45 3.2 1966 Up, Down, Strange, Charm, Tau
Super Proton Synchrotron Ring Proton 450 1.1 1976 W-, Z
Petra Ring Electron 20 .32 1978 Gluon
LEP Collider Ring Electron 104 4.3 1989
Fermilab Ring Proton 1000 6 1989 Bottom, Top
Large Hadron Collider Ring Proton 6500 4.3 2011 Higgs
Compact Linear Collider Linear Electron 3000 30 Future
China proton collider Ring Proton 75000 16 Future
Earth electron collider Linear Electron 30000 300 Far future
Earth proton collider Ring Proton 6000000 1000 Far future
"Collider size" is the radius for ring colliders and half the total length for a linear collider.
"Earth electron collider" is the largest electron linear collider that can be built on the Earth. Its maximum size is set by synchrotron radiation from the Earth's curvature.
"Earth proton collider" is the largest electron linear collider that can be built on the Earth. You need a large continental plate.
The LEP collider was dismantled and its tunnel now hosts the Large Hadron Collider.
 |
|---|
Particle diameter is proportional to Mass1/3.
The electron is exaggerated otherwise it would be invisible.
Blue particles represent the heaviest particle that can be produced by the accelerator.
At this scale, a Planck-mass particle has a diameter of 10 km.
Photons, Gluons, and Gravitons are massless.
The LHC is far from the Planck energy.
 |
|---|
 |
|---|
 |
 |
|---|---|
The energy of a linear accelerator is determined by length and force. The maximum force is .023 TeV/km using klystrons and .1 TeV/km using the dual-beam technique. To discover new physics, the energy has to be larger than 1 TeV. A 1 TeV accelerator based on the dual-beam technique has a length of 10 km.
Accelerator length = X = 10 km Force = F = .1 TeV/km Electron energy = E = X F = 1 TeV
 |
 |
|
|---|---|---|
In a ring collider, magnets steer protons around the ring. Ring colliders can add energy to particles each pass around the ring, and so they aren't limited by force. It's like spinning up a merry-go-round. Ring colliders are limited instead by the strength of the bending magnets. For the Large Hadron Collider,
Magnetic field strength = B = 5.4 Tesla (average field) Radius of the ring = R = 4300 meters Maximum particle energy = E = .00030 B R = 7.0 TeV
If an electron linear collider is long enough, it has to curve with the Earth's surface, and this limits the energy to 23 TeV. You can get to 30 TeV by having a straight section just before the collision.
You can make a long straight tunnel using mountains and by digging deep. The tunnel starts deep and ends at a mountain.
The deepest mines have a depth of 4 km and mountain ranges have a height of order 6 km, and this allows one to build a straight tunnel 100 km long.
The average thermal gradient of the Earth is 25 Celsius per km of depth. The deepest mines are:
Depth Rock temperature
km Celsius
Mponeng Gold Mine 4.0 66 South Africa
TauTona Gold Mine 3.9 60 South Africa
Savuka Gold Mine 3.7 South Africa
Driefontein Mine 3.4 South Africa
 |
 |
 |
|---|---|---|
An accelerating charged particle emits photons (synchrotron radiation). Particles traveling around a ring emit photons and lose energy. The larger the collider, the larger the particle energy and the larger the synchrotron loss rate. A ring collider can only be made so large before synchrotron loss exceeds energy gain from acceleration.
The synchrotron radiation power is
Particle energy = E Particle rest energy = Erest Ring radius = R Synchrotron radiation power = P ~ (E/Erest)4 / R2 Erest (Proton) ------------------- = 1836 Erest (Electron)Electrons have a smaller rest energy than protons and emit vastly more synchrotron radiation. An electron ring collider is limited by synchrotron radiation rather than by magnet strength. The maximum energy is .15 TeV. Generating electron energies larger than this requires a linear collider.
Protons emit negligible synchrotron radiation and the radiation is never a concern. Proton ring colliders are limited by magnet strength rather than by synchtrotron radiation.
Future colliders will consist of proton ring colliders and linear electron colliders.
Particle energy = E (TeV) Particle velocity = V Speed of light = C Particle charge = 1.602e-19 Coulombs Magnetic field = B (Teslas) Magnet strength averaged around the ring Collider radius = R Particle rest mass = m Particle relativistic mass = M Electric force constant = K = 8.988⋅109 Newton meter2 / Coulomb2 Electric force on a charge = Fe = q E Magnetic force on a charge = Fm = q V B Centripetal force = Fc = M V2 / RParticles in a collider are "ultrarelativistic" and so we may assume:
M >> m V ~ C E ~ M C2Particles are steered around the ring by magnets
Magnetic force = Centripetal force q B V = M V2 / R q B = E / (C R) E = q C B R E = .00030 B R (Energy in TeV)The maximum energy of a ring collider is determied by the magnetic field and the ring radius.
Magnets are a finicky technology and thus far the LHC magnets are not at full strength. The current proton energy is 4 TeV and an energy of 6.5 TeV is expected in 2015.
The Lorentz factor of a 7 TeV proton is γ = E/(mC) = 7460 = 7 TeV / .000938 TeV
If a charged particle is accelelerated it emits photons (synchrotron radiation). Particles in a ring collider emit synchrotron radiation when they are bent by the magnetic field.
Particle energy = E
Particle rest energy = Eo
Particle charge = q
Particle velocity = V
Speed of light = C
Electric force constant = K = 8.988⋅109 Newton meter2 / Coulomb2
Collider radius = R
Synchrotron power = P = (2C/3) K q2 (V/C)4 (E/Eo)4 R-2
Decelerating synchrotron force= Fs = P/V (Joules/meter)
Synch. energy loss / cycle = Es = (2πR/V) P Energy lost to synch. each ring trip
= (4πC/3V) K q2 (V/C)4 (E/Eo)4 R-1
~ (4π/3) K q2 (E/Eo)4 / R (Using V ~ C)
Fraction energy lost per cycle= Q = Es / E
Collider maximum energy = Emax
In order for a ring to be effective it must have Q << 1. If Q >= 1 then you might
as well build a linear collider. For a given collider radius R the synchrotron
energy limit is
Emax = Es / Q = (4/3 πKq2/Q) (Emax/Eo)4 R-1 Q-1
= (4/3 πKq2/Q)-1/3 Eo4/3 R1/3
The CERN ring has R = 4243 meters. If we set Q=1 we get the following energies:
Eo Emax
(TeV) (TeV)
Electron .000511 .27
Muon .106 325
Proton .938 5961
When the CERN ring housed the Large Electron Positron collider (LEP) it operated
at an energy of .104 TeV. The ring was subsequently converted to a proton collider
with an energy of 7 TeV. Proton synchrotron radiation is negligible at this energy.
The energy limit from synchrotron radiation has the form: E ~ R1/3 The energy limit from the bending magnets has the form: E ~ B RWhen these are equal, the energy and radius are "Er" and "Rr".
If R < Rr then E is limited by the strength of the magnets If R > Rr then E is limited by synchrotron radiationIf we set B = 10 Tesla and Q = 1 we get
Er (TeV) Rr
Electron .061 20 meters
Muon 2630 880 km
Proton 207000 69000 km = 11 Earth radii
An electron collider larger than 20 meters is limited by synchrotron radiation.
Any proton or muon collider that could conceivably be built on the Earth is limited by the bending magnets rather than by synchrotron radiation.
In a collider, a particle "X" collides with its antiparticle "x" and they annihilate to create a new particle-antiparticle pair Y and y.
X + x --> Y + yThe maximum rest mass of the Y particle is equal to the energy of the X particle. Hence, a collider that collides 1 TeV electrons with 1 TeV antielectrons can produce particles with a rest mass of up to 1 TeV.
Protons consist of three quarks. In a proton collision, new particles are produced by collisions between individual quarks. Since each quark carries only a fraction of the proton's total energy, not all of the proton's energy can be used to make new particles. At Fermilab, protons have an energ of 1 TeV and the heaviest particles it can create are the .171 TeV top quark and the .125 TeV Higgs boson. This gives electron and muon colliders an energy edge over proton colliders.
Electron and muon colliders can also tune the beam energy to be exactly equal to the rest energy of the particle they're trying to create, whereas the energy of a quark-quark collision can't be tuned. This means that electron and muon colliders can produce particles with greater rates than a proton collider.
Electron and muon collisions also produce less background particles than proton collisions, making the events easier to analyze.
If a collider follows the curvature of the Earth then the synchrotron energy limit is:
Collider radius = R = 6.371⋅106 meters (For the Earth) Particle energy = E = 23 TeV (For electrons limited by the Earth's curvature) Particle rest energy = Eo = .00000051 TeV (Electrons) Forward accelerating force = Fc = .0001 TeV/m (For the Compact Linear Accelerator) Synchrotron decelerating force = Fs = (2/3) K q2 (E/Eo)4 / R2If the collider force is equal to the synchrotron force,
E = Eo Fc1/4 R1/2 [(2/3) K q2]-1/4The following table gives the synchrotron energy limit for electrons, protons, and muons.
Radius Electron Muon Proton
TeV TeV TeV
Earth surface 6371 km 23 4800 43000
Orbit around Earth 10000 km 29 6000 53000
Earth orbit around sun 1.2 AU 6000 850000 7500000
Kuiper Belt orbit around sun 40 AU 53000 4700000 41000000
Light year radius 63200 AU 2109000 187060000 1630000000
Muons have a halflife of 2.2 microseconds. Muons in a collider live longer because of time dilation, and so they can traverse the ring many times before decaying.
Muon halflife = T = 2.2e-6 seconds
Collider radius = R
Magnetic field = B
Muon energy in TeV = E = .00030 B R (from the "ring colliders" section)
Muon Lorentz factor = Z = E / .000106 = E / Restenergy
Speed of light = C
Ring cycles = N = Z T C / (2 π R) (Trips around the ring in one halflife)
= (.00030 B R / .000106) T C / (2 π R)
= 297 B
A future muon collider would have B ~ 10 Tesla, and so the muons will traverse the
ring ~ 3000 times before decaying.
The obstacle to building a muon collider is the need for a muon cooling technology, currently under development at Fermilab. If this can be done, then muons could be used at the Large Hadron Collider.
Muons emit high-energy neutrinos, which is a hazard to nearby humans. A set of sample radiation parameters can be found in http://arxiv.org/pdf/hep-ex/0005006v1.pdf
Muon energy Radiation
(TeV) (mSieverts/yr)
2 .0005
5 2.3
50 10
Earth average background radiation is 3.5 mSieverts/yr. A muon collider with
energy > 5 TeV would have to be located at a remote site away from
civilization.
These are hypothetical colliders that could be built in the near or distant future. We assume a gradient of .1 TeV/km for linear colliders and a magnetic field of 10 Tesla for ring colliders.
Particle Shape Length or Energy
Radius (km) (TeV)
Electron Ring 13 .125 Higgs energy, to mass-produce the Higgs
Electron Linear 30 3 Compact Linear Collider
Proton Ring 4.2 7 Existing LHC
Electron Linear 800 80 Limited by synchrotron radiation from the Earth's curvature
Muon Linear 4000 400
Proton Ring 1000 600 Continent-sized
Electron Linear 1 AU 4200 Orbiting the sun between Earth and Mars. synchrotron limit
Muon Ring 10000 6000 Orbiting the Earth
Muon Ring 1 AU 106 Orbiting the sun between Earth and Mars. synchrotron limit
Muon Ring 100 AU 107 Orbiting the sun at the Kuiper belt, synchrotron limit
Muon Linear 1 LY 1012
An advanced civilization will likely find a way to improve the energy gradient, and hence a light year sized collider will likely reach the strong scale energy of 1013 TeV. Reaching the Planck energy of 1016 requires a substantial improvement in the energy gradient, or a colossally long collider.
The Planck energy is 1016 TeV. If the energy gradient is .1 TeV/km then the collider length is 1017 km = 10000 light years. This is 1/3 of the distance between the sun and the center of the Milky Way. Such a collider would have to be built in intergalactic space to escape the gravity of galaxies.
Collider Particle Type Energy Size Lum Power BeamX BeamY BeamZ Particles/ Particles/
TeV km MW nm nm nm second (1024) bunch
Stanford Linear Accel. e- Linear .045 3.2 .0003 64 2000 2000 .12
Large Electron Positron e- Ring .104 4.3 .01 18 200000 2000 3600.
Fermilab Proton Ring 1.0 1.0 .04 30000 30000
Large Hadron Collider Proton Ring 7 4.3 1 17000 17000 44000 29000.
Int. Linear Collider e- Linear .5 16 2 230 5.7
Compact Linear Collider e- Linear 3 30 6 240 40 1 .024
Higgs factory e- Ring .125 8.5 1.8 50
"Size" corresponds to radius for a ring collider and length for a linear collider.
"Lum" is the luminosity in 10^34 particles / cm2 / s
BeamX is the horizontal beam size
BeamY is the vertical beam size
Linear colliders tend to have a smaller beam cross section than ring colliders.
The "Circular Electron Positron" collider is a future collider that is optimized for generating Higgs particles.
Suppose we compare the tunnel lengths of a linear and a ring collider.
In an electron-positron collision, all of the particle energy can be harnessed for creating new particles. In a proton-proton collision, only a fraction of the energy is available for creating new particles.
Linear collider radius = Rl = 500 km
Linear collider energy gradient = G = .1 TeV/km
Linear collider energy = El = Rl G = 50 TeV
Ring collider radius = Rr = 83 km
Ring collider mean magnetic field = B = 10 Tesla
Ring collider constant = C = .30 TeV/Tesla/km
Ring collider reach factor = f = .2
Ring collider energy = Er = C B Rr = 250 TeV
= El/f
Radius ratio = Q = Rr/Rl = G (f C B)-1 = .17 for protons
= .033 for muons
What is the interplanetary magnetic field as a function of distance from the sun? What would you estimate is the lowest-energy cosmic ray that can reach the Earth from interstellar space?
 |
|---|