





 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|
 |
 |
 |
 |
|---|---|---|---|
Flying electric cars are easy because lithium-ion batteries have a good power to mass ratio. For 1-person flying car, the minimum power/mass required to hover is 200 Watts/kg and a lithium-ion battery can produce 1000 Watts/kg.
Electric motors contribute neglibly to the mass of the car because they have a power/mass much larger than the battery (7000 Watts/kg). The propeller weighs even less than the motor.
Because motors are easy, a flying vehicle can have many motors and propellers, which helps with safety. Also, the more propellers a vehicle has, the easier it is to fly, because it reduces the minimum power/mass required to fly.
Electric motors are simpler and safer than gasoline motors. Gasoline motors come with baggage like gears, powertrains, combustion, flywheels, mufflers, etc., none of which are present in electric motors.
For a 1-person flying car,
Power/Mass
Watts/kg
Minimum for fixed-wing flight 120
Minimum for hovering flight 200
Minimum vehicle power/mass 300 = pveh Should be easily able to hover. Use 1.5 times the minimum to hover
Lithium-ion battery 1000 = pbat
To hover, the battery mass has to be at least 3/10 the vehicle mass to provide enough power. The minimum battery mass fraction is pbat/pveh = 3/10.
Since a lithium-ion battery can easily power a hoovering vehicle, vertical takeoff is easy. There is no niche for a runway-based car.
The battery can be made larger to increase range. For fixed-wing flight, an electric flying car has a cruising speed of 50 meters/second and a range of 150 km.
Lithium-ion battery energy/mass= e = 1.0 MJoule/kg Minimum for fixed-wing flight = pfix = 100 Watts/kg Battery mass fraction = f = .3 Flying time = T = f e/pfix = 3000 seconds Fixed-wing cruising speed = V = 50 meter/second Range = X = V T = 150 km
An electric generator has a power/mass of 200 Watts/kg, too small to fly. A small detachable electric generator could be potentially added for recharging off grid.
For flight at constant velocity,
Number of propellers = N Hovering minimum power/mass = p ~ M1/6 N-1/6 Fixed-wing cruising speed = V ~ M1/6 Fixed-wing cruising flight time= T ~ M-1/6 Fixed-wing cruising range = X ~ M0
A single-person aircraft has a mass of ~ 400 kg and a hovering minimum power/mass of 200 Watts/kg. A 1 kg drone has a hovering minimum power/mass of 74 Watts/kg.
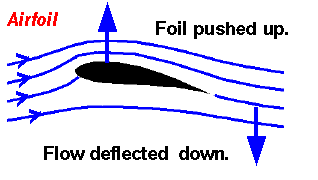
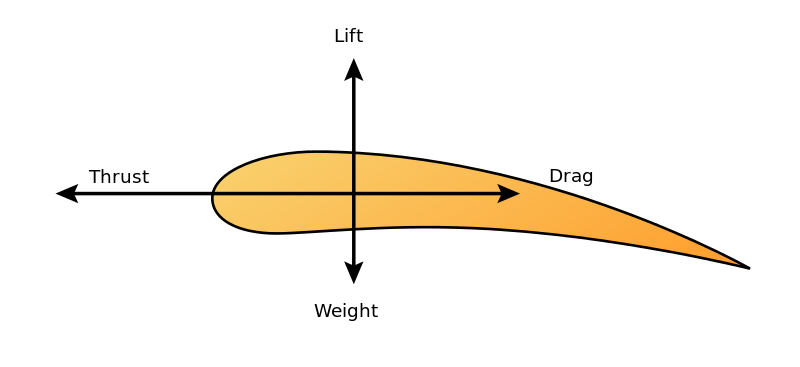
An wing generates lift at the cost of drag. Lift exceeds drag.
 |
 |
|---|---|
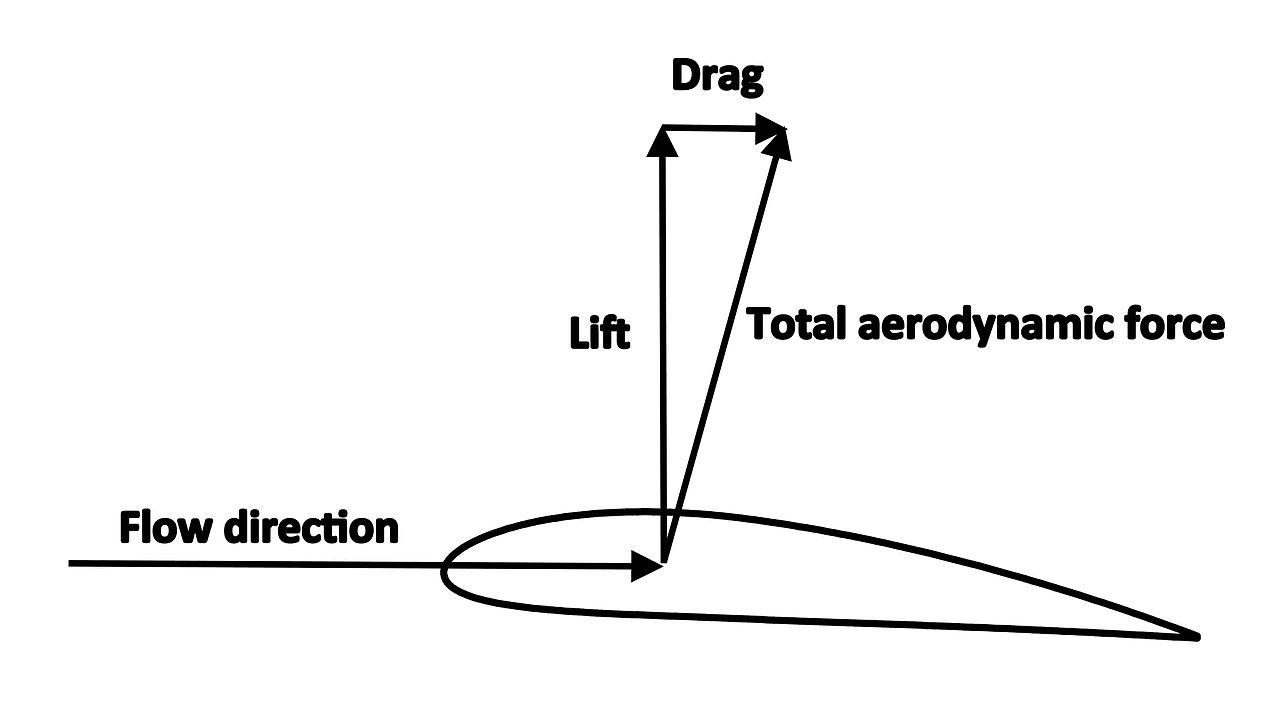
Wing drag force = F→ Wing lift force = F↑ Wing lift-to-drag coef.= Qw = F↑ / F→
The lift-to-drag coefficient Qw is proportional to wing length divided by wing width.
Wing length = L Wing width = W Wing lift-to-drag coef.= Qw ~ L/W = Wing aspect ratio.
Wing width varies along the length of the wing. We define an effective width as
Width = ½ Area / Length
"Area" is the total for both wings, and "Length" is for one wing.
Aspect ratio is Length/Width.
Qw Aspect Wing Wing Wing
ratio length width area
meter meter meter2
U-2 23 10.6 High-altitude spy plane
Albatros 20 1.7 Largest bird
Gossamer 20 10.4 14.6 1.4 41.3 Gossamer albatross, human-powered aircraft
Hang glider 15
Tern 12
Herring Gull 10
Airbus A380 7.5 7.5 36.3 11.6 845
Concorde 7.1 .7 11.4 15.7 358.2
Boeing 747 7 7.9 23.3 11.3 525
Cessna 150 7 2.6 4.5 1.7 15
Sparrow 4
Human wingsuit 2.5 1 1.0 1.0 2
Flying lemur ? Most capable gliding mammal. 2 kg max
Flying squirrel 2.0
 |
|
|---|---|
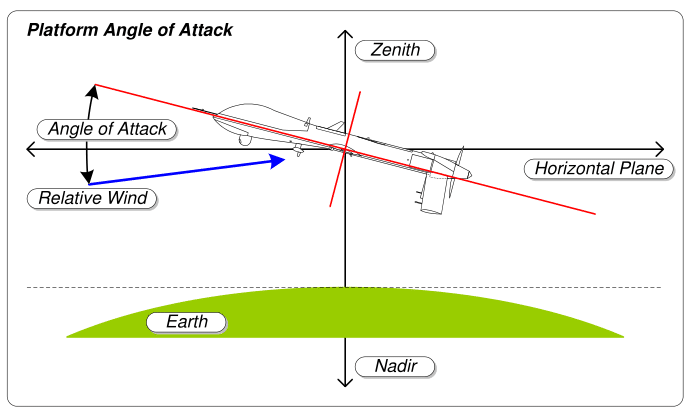
Changing wing angle changes lift and drag. There is an optimum angle that maximizes the lift-to-drag coefficient.
If the angle is larger than the optimal angle, you gain lift at the expense of drag. If you make the angle of attack too large, lift ceases and the plane stalls.
The air drag force is
Air density = D = 1.22 kg/meter2 Velocity = V Cross-sectional area = A Drag coefficient = C Drag force = F = ½ C D A V2
Human mass = M = 80 kg Gravity = g = 10 meter/second2 Gravity force = F↓ = 800 Newton Chute drag coefficient = C = 1 Dimensionless Air density = D =1.22 kg/meter2 Parachute area = A = 100 meter2 Drag force = F↑ = ½ C D A V2 = F↓ Terminal velocity = V = 3.6 meter/second
Drag force = F = ½ C D A V2 Drag power = P = F V = ½ C D A V3
Drag coef Drag area Power Max speed
dimensionless meter2 Watt meter/second
Bike 1 .5 400 11
Car .4 3 300000 74
Cw
F-4 Phantom .021 (subsonic)
Cessna 310 .027
Airbus A380 .027
Boeing 747 .031
F-4 Phantom .044 (supersonic)
 |
|---|
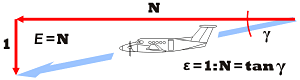
A glider is unpowered. The more efficient the glider, the smaller the glide angle. The minimum glide angle is determined by the wing lift/drag coefficient.
Drag force = F→ Lift force = F↑ = Fgrav Wing lift/drag ratio = Qw = F↑ / F→ Horizontal speed = V→ Vertical descent speed = V↓ Glide ratio = G = V→ / V↑ Gravitational force = Fgrav Drag power = Pdrag = F→ V→ Power from gravity = Pgrav = Fgrav V↓If the glider descends at constant velocity,
Pdrag = PgravThe goal of a glider is to maximize the glide ratio
V→ / V↓ = (Pdrag / F→) / (Pgrav / Fgrav)
= Fgrav / F→
= Qw
The glide ratio is equal to the lift coefficient. Qw = G
 |
|---|
Air density = D Wing area = A Wing drag coefficient = Cw Wing drag = F→ = ½ Cw D A V2 Wing lift = F↑ Wing lift/drag ratio = Qw = F↑ / F→ Aircraft speed = V Aircraft mass = M Gravity = g = 9.8 meters/second2 Gravity force = Fgrav= M g Engine force = Feng = V F→ Drag power = P→ = F→ V = ½ Cw D A V3 Agility (Power/mass) = p = P→ / M = V g / QwFor flight at constant velocity,
Feng = F→ Horizontal force balance F↑ = Fgrav Vertical force balance F↑ = F→ Qw Definition of the wing lift/drag coefficient Fgrav= Fdrag Qw → M g = Qw ½ Cw D A V2 Cruising speed = V = M½ g½ Qw-½ (½ Cw D A)-½ ~ M1/6 Agility (Power/mass) = p = M½ g3/2 Qw-3/2 (½ Cw D A)-½ ~ M1/6 Aircraft energy/mass = e ~ M0 Flight time = T = e/p ~ M-1/6 Range = X = V T ~ M0
For the mass scalings, we assume that wing area scales as M2/3.
 |
|---|
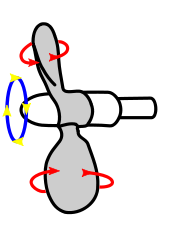
A wingtip creates a vortex as it moves. Wingtips are often equipped with a vertical element to damp the vortex. The vertical element increases the effective wing length and improves the lift-to-drag coefficient. coefficient.
Birds fly in a "V" formation to use the updraft from their neighbor's wingtip vortices.
 |
|---|
For propellers,
Rotor radius = R
Air density = D = 1.22 kg/meter3 at sea level
Rotor tip speed = V
Rotor width param= Cr
Rotor lift force = F↑ = D Cr R2 V2
Rotor drag force = F→
Rotor lift/drag = Qr = F↑ / F→
Rotor power = P = F→ V = F↑ V / Qr
Rotor force/power= Z = F↑/ P
= Qr / V
= R F↑-½ D½ Cr½ Qr
= R F↑-½ D½ qr
Rotor quality = qr = Qr Cr½
The physical parameters of a propeller are {Qr,Cr,qr}, with typical values of
Qr = 5.5 Cr = .045 qr = 1.17Most propellers have 2 blades and some have 3. If there are 4 or more blades then qr declines.
The parameters are not independent. They're related through the blade aspect ratio.
K ≈ Aspect ratio Cr ≈ K-½ Qr ≈ K qr ≈ K½
Aircraft mass = M Gravity = g Aircraft force = F↑ = M g Rotor radius = R ~ M1/3 Hovering force/power = Z = qr D½ R F↑-½ ~ M-1/6 Hovering power/mass = p = g / Z ~ M1/6 Aircraft energy/mass = e ~ M0 Hovering time = T = e / p ~ M-1/6
A drive propeller has to move substantially faster than the aircraft to be effective. This distinguishes it from a hovering propeller, which is designed to minimze propeller speed.
Rotor radius = R Air density = D = 1.22 kg/meter3 Aircraft speed = U Rotor speed coef. = s Rotor tip speed = V = s U Rotor lift force = F↑ Rotor drag force = F↓ Rotor lift/drag = Qr = F↑ / F↓ Rotor power = P = F↓ V = F↑ V / Q Rotor force/power = Z = Q / VTypically, Q ~ 5.5 and s ~ 3.
A commonly-appearing quantity is the power/mass ratio, which is inversely proportional to the force/power ratio.
Mass = M Gravity = g Rotor quality = q Hover force = F = M g Hover power = P Force/Power ratio = Z = F/P Power/Mass ratio = p = P/M = g/Z
Air density = Dair= 1.22 Seawater density = Dwater= 1025 Gravity = g = 9.8 meters/second2 Wing drag coef. = Cw = .03 Wing Lift/drag = Qw = 7 Rotor lift/drag = Qr = 5.5 Rotor width param = Cr = .045 Rotor quality = qr = 1.17 = Qr Cr½ Rotor force/power = Zr Rotor agility = pr = g/Zr Wing agility = pw
Aircraft mass = M Gravity = g Air density = D = 1.22 kg/meter3 Aircraft speed = U Rotor speed coef. = s Rotor tip speed = V = s U Aircraft lift force = F = M g Rotor lift force = F↑ Wing lift/drag = Qw = F / F↑ Rotor drag force = F→ Rotor lift/drag = Qr = F↑ / F→ Rotor power = P = F→ V = F↑ V / Qr = F V / (Qr Qw) Aircraft force/power = Z = F / P = [Qr Qw / s] / UThere is a tradeoff between Qr and s.
The larger the number of rotors, the less power is required to fly. The efficiency of a rotor is characterized by the force per power.
Number of rotors = N
Aircraft mass = M
Total rotor mass = m
Rotor mass = m/N
Rotor constant = C
Rotor radius = R = C m1/3 N-1/3
Gravity = g
Force per rotor = F = Mg/N
Rotor quality = q = 1.17
Air density = D = 1.22
Rotor quality = Q = q D½ = 1.29
Rotor force/power = q D½ C (m/N)1/3 (Mg/N)-½
= q D½ C N1/6 m1/3 M-½ g-½
For example, in dimensionless units,
Rotors Rotor Rotor Rotor Rotor
mass radius force force/power
1 1 1 1 1
2 .5 .79 .5 1.12
3 .33 .69 .33 1.20
4 .25 .63 .25 1.26
6 .167 .55 .167 1.35
8 .125 .50 .125 1.41
16 .062 .40 .062 1.59
 |
|---|
Altitude Density
(km) (kg/m3)
Sea level 0 1.22
1 1.14
2 1.02
Cessna 150 3 .79
Mount Everest 8.8 .46
Boeing 747 11.0 .36
Airbus A380 13.1 .26
Concorde 18.3 .115
F-22 Raptor 19.8 .091
U-2 21.3 .071
SR-71 Blackbird 25.9 .034
Energy/Mass Power/Mass Recharge Year Anode Cathode Market fraction of
MJoule/kg Watt/kg Lithium-ion batteries
Lithium air 6.12 No Future Li O2
Aluminum air 4.68 200 No 1970 Al O2
Lithium thionyl 2.00 700 No 1973 Li SOCl2
Zinc air 1.59 No 1932 Zn O2
Lithium-ion sulfur 1.44 670 Yes Future Li S 0
Lithium metal 1.01 400 No 1976 Li MnO2
Lithium-ion CoNiAlO2 .79 Yes 1999 Li CoNiAlO2 .10
Lithium-ion CoNiMnO2 .74 1200 Yes 2008 Li CoNiMnO2 .29
Lithium-ion CoO2 .70 200 Yes 1991 Li CoO2 .29
Lithium-ion Mn2O4 .54 1200 Yes 1999 Li Mn2O4 .10
Lithium-ion FePO4 .47 1200 Yes 1996 Li FePO4 .22
Alkaline .40 Yes 1992 Zn MnO2
NiMH .34 1000 Yes 1990 MH NiO(OH)
Lead acid .15 180 Yes 1881 Pb PbO2
NiCd .14 200 Yes 1960 Cd NiO(OH)
Voltage = V Volts
Charge = C Coulombs
Time = T seconds
Electric current = I = C/T Amperes (Amps)
Electric power = P = VI Watts
Energy = E = PT Joules
= CV Joules
Battery energy is often given in "Watt hours" or "Ampere hours".
1 Watt hour = 3600 Joules = 1 Watt * 3600 seconds
1 Amp hour = 3600 Coulombs = 1 Coulombs/second * 3600 seconds
A battery with a voltage of 3.7 Volts that delivers
1 Ampere for 1 hour has an energy of
Energy = 1 Ampere * 3.7 Volts * 3600 seconds = 13320 Joules
 |
|---|
Energies and powers are for lithium batteries, which have a voltage of 3.7 Volts. The "ID #" is often used instead of cell size.
Cell Energy Power Current Mass Diameter Length Charge Price ID # size kJoule Watt Ampere gram mm mm AmpHour $ D 107 220 60 138 32 67 8.0 13 32650 C 67 220 60 92 26 50 5.0 8 26650, 25500 B 58 160 45 72 22 60 4.5 5 21700, 20700 A 47 110 30 49 18 50 3.5 3 18650 AA 9 22 6 15 14 53 .70 1 14500 AAA 4.7 11 3 7.6 10 44 .35 .5 10440 AAAA 2.3 6 1.5 3.8 8 42 .17 .25 75400 CR2032 3. Most common button cell CR1216 .33 Smallest button cell Apple Watch 4 4.0 .29 iPhoneXR 6" 41 2.94 Machine = .194 kg iPhoneXSM 6" 44 3.17 Machine = .208 kg iPhoneXS 6" 36 2.66 Machine = .177 kg iPhone8+ 6" 27 2.79 Machine = .202 kg iPhone8 5" 25 1.82 Machine = .148 kg iPhone7+ 6" 40 2.90 Machine = .188 kg iPhone7 5" 27 1.96 Machine = .138 kg iPad Mini 8" 70 5.12 Machine = .30 kg iPad Pro 10" 111 8.13 Machine = .47 kg Mac Air 11" 137 Machine = 1.08 kg Mac Air 13" 194 Machine = 1.34 kg MacBook 12" 149 Machine = .92 kg Mac Pro 13" 209 Machine = 1.37 kg Mac Pro 15" 301 Machine = 1.83 kg
Energy Power Lifetime
kJoule Watts hours
iPhone 8 5" 25 .50 14
iPhone 8+ 6" 27 .54 14
iPad Mini 8" 70 1.9 10
iPad Pro 10" 111 3.1 10
Mac Air 11" 137 3.8 10
Mac Air 13" 194 5.4 10
Mac Pro 13" 209 5.8 10
Mac Pro 15" 301 8.4 10
A single battery is a "cell" and a set of cells is a "pack". Packs are used to multiply the energy and power of cells.
Battery packs are notorous for catching fire, but cell technology has reached the point where it's now possible to make safe battery packs, and the design is simple enough so that anyone can construct their own packs.
Cells can be combined in series and/or parallel. Connecting in series multiples voltage, and voltage is helpful for achieving high power in a motor.
Connecting in series is easier than in parallel. If it's possible to achieve the required power without parallelization then one should do so, and this is usually possible with modern cells.
Series packs have the advantage that the cells can easily be extracted and charged individually, and cells can be interchanged between packs. One can also construct a set of series packs and swap them in like gun clips.
High power electric bikes use a voltage of 72 Volts. If we use one series array of C cells then a pack provides 4440 Watts and 1.2 MJoules. Any electric device requiring less than this much power can be powered by a series pack.
The properties of a modern high-power cell are:
Type = "C" Voltage = 3.7 Volts Energy = 60 kJoules Power = 155 Watts Mass = 92 grams Energy/mass = 650 kJoules/kg Power/mass =1680 Watts/kg Current = 42 Amperes Manufacturer = "Basen"When the cells are connected in series the values for voltage and power are:
Cells Voltage Power
Volts kWatts
1 3.7 .15
2 7.4 .30
3 11 .45 Electric kick scooter
4 15 .60
6 24 .90 Electric bike
10 36 1.5
20 72 3.0 Compact electric car
96 356 15.0 Large electric car
Size Charge Current Price
Amphours Amps $
Basen C 4.5 60 8.0
Panasonic B 4.0 15 8.0
Sony VTC6 A 3.0 30 8.0
Panasonic A 3.5 10 5.5
Efest IMR AA .65 6.5 3.5
Efest IMR AAA .35 3 3.0
Prices from www.liionwholesale.com
 |
|---|