





 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|
A (B C) = (A B) C Associativity A B = B A Commutivity (A + B) C = A C + B C Distributivity CAB = CA CB logC(A B) = logC(A) + logC(B)
1! = 1 2! = 2 = 2⋅1 3! = 6 = 3⋅2⋅1 3! = 24 = 4⋅3⋅2⋅1 x! = x (x-1) (x-2) ... 1
(x+y)2 = x2 + 2 xy + y2 (x+y)3 = x3 + 3 x2y + 3 xy2 + y3 (x+y)4 = x4 + 4 x3y + 6 x2y2 + 4 xy3 + y4
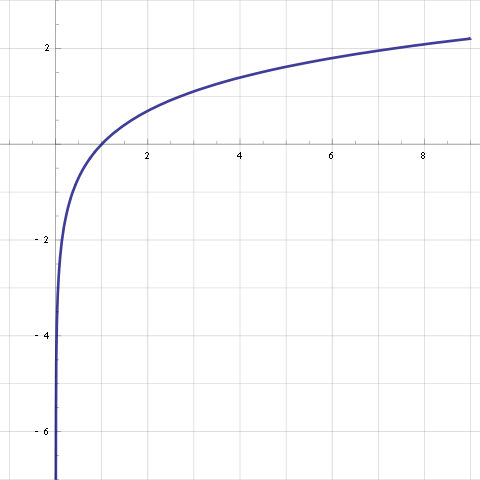
The exponential function is
exp(x) = ex e = 2.718281828459...The exponential function has the property that
∂x ex = ex e = ∑n=0∞ 1 / n! = 1 + 1/2 + 1/6 + 1/24 + ...
 |
|---|
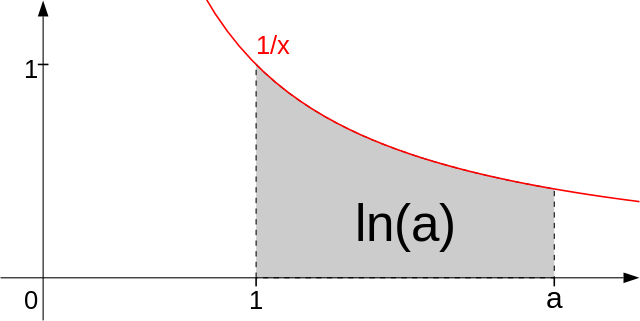
The logarithm is the inverse of the exponential function.
10-2 = .01 log10 .01 = -2 10-1 = .1 log10 .1 = -1 100 = 1 log10 1 = 0 101 = 10 log10 10 = 1 102 = 100 log10 100 = 2 10log10x = log10 10x = 1 eln x = ln ex = 1
Two integers are "relatively prime" if they have no common factors that are larger than 1. For example, "4" and "6" are not relatively prime because they share the factor "2", and the numbers "3" and 5" are relatively prime because they have no common factors.
i = √-1 X = Xr + Xi i = Xm eiXθ = cos(θ) + sin(θ) i Xm = (Xr2 + Xi2)½ tanθ= Xi/Xr A = Ar + Ai i = Am eiAθ B = Br + Bi i = Bm eiAθ A B = Ar Br - Ai Bi + (Ai Br + Ar Bi) i= Am Bm ei(Aθ+Bθ)
 |
|---|
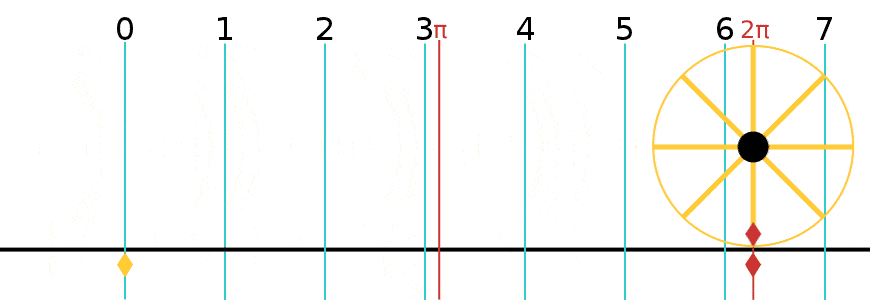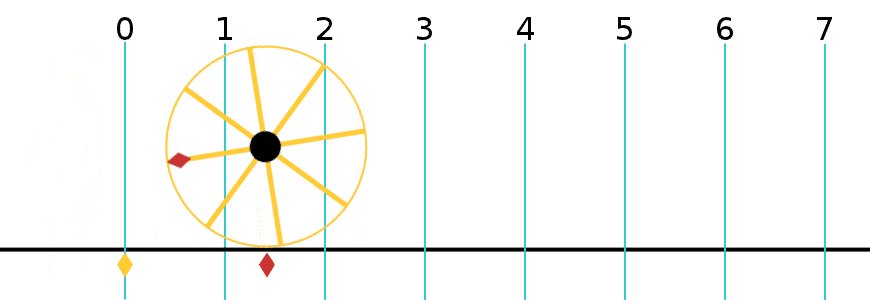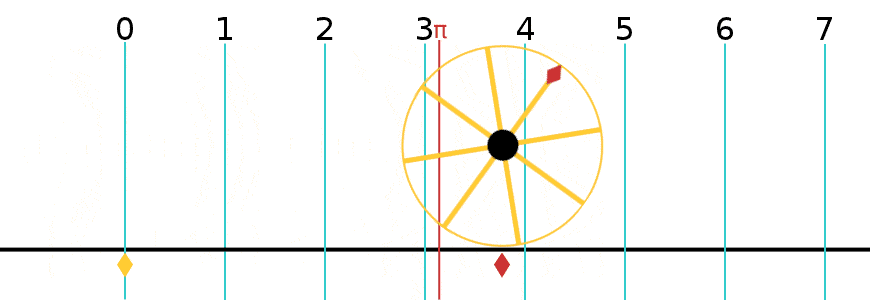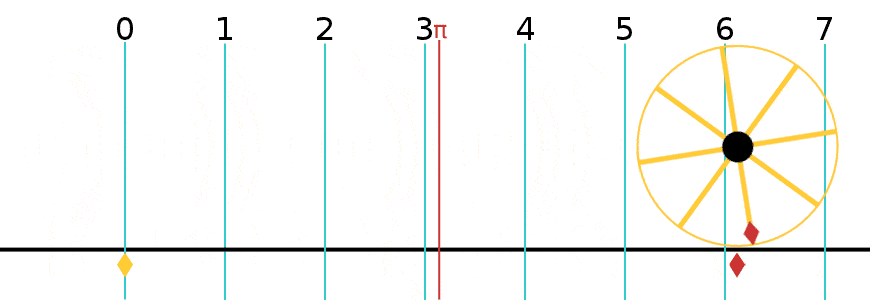
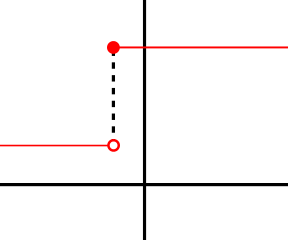
= Angle in radians (dimensionless) X = Arc distance around the circle in meters (the red line in the figure) R = Radius of the circle in meters X = R
 |
 |
|---|---|
Pi is defined as the ratio of the circumference to the diameter.
Full circle = 360 degrees = 2 radians 1 radian = 57.3 degrees 1 degree = .0175 radians
 |
|---|
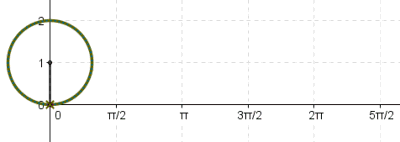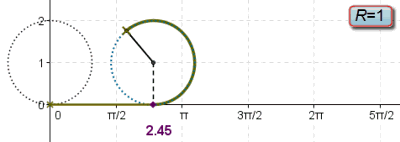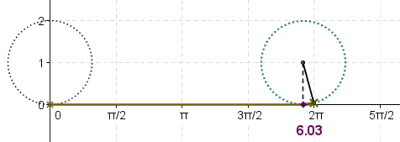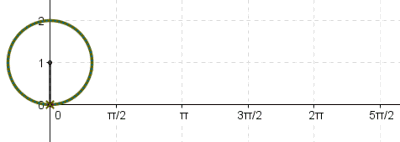
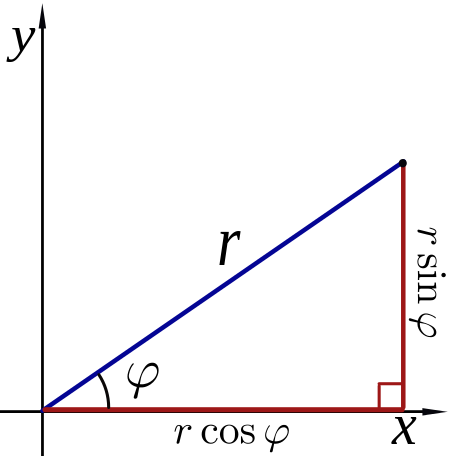
Radius = R Angle = X coordinate = X = R cos(θ) Y coordinate = Y = R sin(θ) tan(θ) = sin(θ) / cos(θ)
Let (X,Y) be a point on a circle of radius R.
θ = Angle of the point (X,Y) in radians X = R cos(θ) Y = R sin(θ) Y/X = tan(θ)If θ is close to zero then
X ~ R Y << X Y << R sin(θ) ~ θ tan(θ) ~ θThe "small angle approximation" is
Y/X ~ θ
10 2 4 8 16 0 0 0 0 0 1 1 1 1 1 2 10 2 2 2 3 11 3 3 3 4 100 10 4 4 5 101 11 5 5 6 110 12 6 6 7 111 13 7 7 8 1000 20 10 8 9 1001 21 11 9 10 1010 22 12 A 11 1011 23 13 B 12 1100 30 14 C 13 1101 31 15 D 14 1110 32 16 E 15 1111 33 17 F 16 10000 40 20 10 17 10001 41 21 11 18 10010 42 22 12 19 10011 43 23 13 20 10100 44 24 14
If an object starts at X=0 and moves with constant velocity,
Time = T (seconds) Velocity = V (meters/second) Distance traveled = X = V T (meters)
 |
|---|
In the previous case the acceleration is 0.
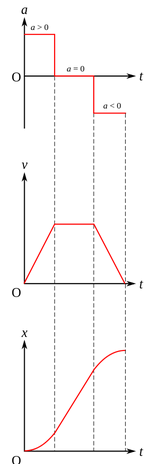
If an object starts at rest with X=0 and V=0 and moves with constant acceleration,
Time = T (seconds) Acceleration = A (meters/second2) Final velocity = V = A T (meters/second) Average velocity = Va = .5 V (meters/second) Distance traveled = X = Va T = .5 V T = .5 A T2 (meters)All of these equations contain the variable T. We can solve for T to obtain an equation in terms of (X, A, V).
V2 = 2 A XSim: Position, velocity, and acceleration
There are four variables (X, V, A, T) and four equations, and each equation contains
three of the variables.
At T=0, X=0 and V=0.
Equations Variables in Variable not
the equation in the equation
V = A T V A T X
X = .5 A T2 X A T V
X = .5 V T X V T A
V2 = 2 A X X V A T
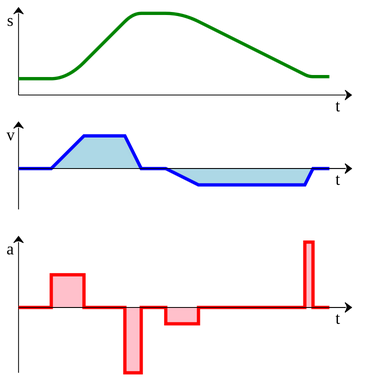
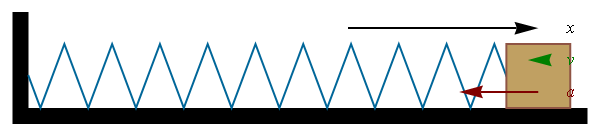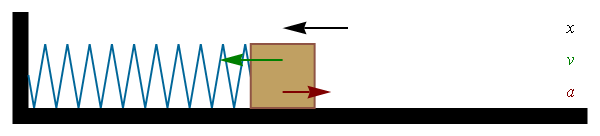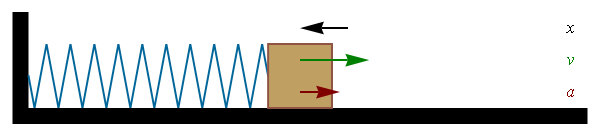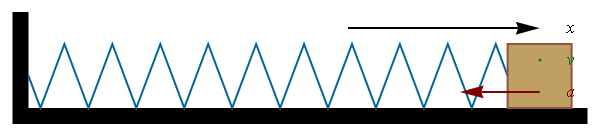
The figure shows the position of a ball at regular time intervals and the green arrow shows the direction of the acceleration.
Top row Zero acceleration (constant velocity) Second row Positive acceleration Third row Negative acceleration (deceleration) Fourth row Free-fall in gravityIn the language of calculus,
Time = T Position = X = = V dT Velocity = V = ∂X/∂T = A dT Acceleration = A = ∂V/∂TExamples of position, velocity, and acceleration.
 |
 |
 |
|---|---|---|
Sim: Position, velocity, and acceleration #2
Mass = M Acceleration = A Force = F = M A (Newton's law)
.gif) |
|---|
For an object falling in gravity, the acceleration doesn't depend on mass and the acceleration is the same everywhere on the surface of the Earth.
Mass = M
Gravity constant = g = 9.8 m/s2
Gravity acceleration = A
Gravity force = F = M g (Law of gravity)
= M A (Newton's law)
Cancelling the "M's", the acceleration experienced by the object is
A = gIf gravity is the only force involved, then all objects experience the same gravitational acceleration.
We can distinguish between gravitational mass and inertial mass.
Mgrav = Gravitational mass Minertial = Inertial mass F = Mgrav g Gravitational mass causes gravitational force F = Minertial A Inertial mass governs the response to forceFor all known forms of matter,
Mgrav = Minertial
For this example we set g=10 m/s2 and assume there is no air drag. If an object starts at rest and falls under gravity, the distance fallen is
Time Velocity Average Distance Acceleration
(s) (m/s) velocity fallen (m/s2)
(m/s) (m)
0 0 0 0 10
1 10 5 5 10
2 20 10 20 10
3 30 15 45 10
4 40 20 80 10
Distance fallen = ½ * Acceleration * Time2
limx→∞ x-1 = 0 limx→0 x-1 = ∞ limx→∞ x = ∞ limx→∞ ex = ∞ limx→∞ e-x = 0 limx→∞ ln x = ∞ limx→∞ sin x = DNE limx→∞ sin x = DNE limx→∞ cos x = DNEDNE: The limit does not exist
 |
|---|
 |
|---|
The derivative is defined as
∂x f(x) = limδ→0 [f(x+δ) - f(x)] / δ if this limit existsFor example,
∂x x = limδ→0 [(x+δ) - x] / δ = 1Notation:
∂x [∂x f(x)] = ∂x2 f(x) ∂x f(x) = f'(x) ∂x2 f(x) = f"(x) ∂x3 f(x) = f‴(x) ∂x4 f(x) = f""(x)
Time = t Position = x(t) Velocity = v(t) = ∂t x(t) Acceleration = a(t) = ∂t v(t) = ∂t2 x(t)
"a" is a constant and "x" is the veriable being differentiated
∂x a = 0 ∂x x = 1 ∂x x2 = 2 x ∂x x3 = 3 x2 ∂x x4 = 4 x3 ∂x xn = n xn-1 ∂x ex = ex ∂x ln(x) = x-1 ∂x sin(x) = cos(x) ∂x cos(x) = -sin(x)
 |
 |
|---|---|
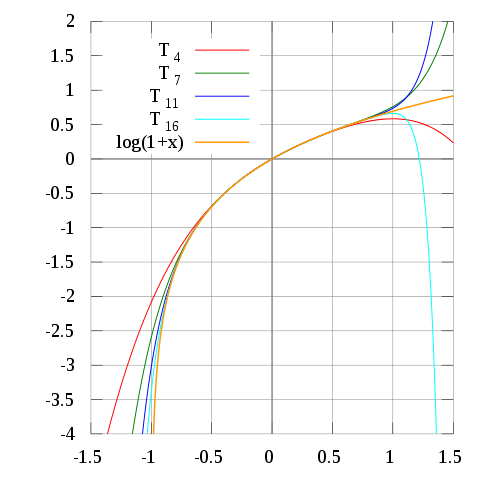
f(x) = f(0) + f'(0) x + (2!)-1 f"(0) x2 + (3!)-1 f‴(0) x3 + (4!)-1 f""(0) x4 + ... ex = 1 + x + (2!)-1 x2 + (3!)-1 x3 + (4!)-1 x4 + ... ln (1+x) = x - 2-1 x2 + 3-1 x3 - 4-1 x4 + ... sin x = x - (3!)-1 x3 + (5!)-1 x5 - (7!)-1 x7 + ... cos x = 1 - (2!)-1 x2 + (4!)-1 x4 - (6!)-1 x6 + ...
∂x (A B) = (∂xA) B + A (∂xB)
"C" denotes an arbitrary constant.
∂x Y = Y → Y = C ex ∂2x Y = -Y → Y = C1 sin(x) + C2 cos(x)
 |
 |
|---|---|
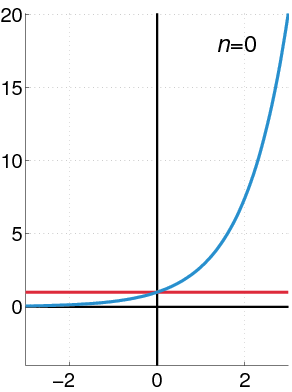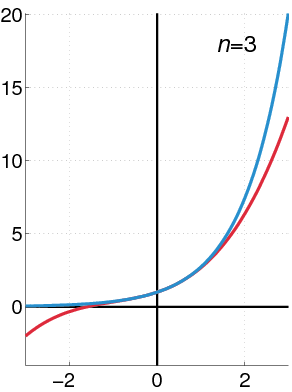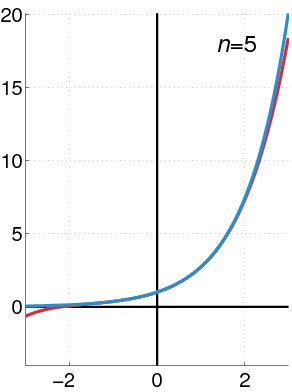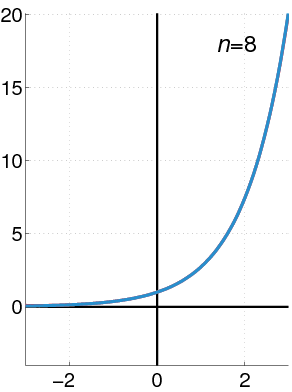
ex = limn→∞ (1 + x/n)n
Getting the correct answer is only worth half the points. For full credit, you must give a rigorous proof.
What are the last 2 digits of
33333
Note that exponentials are evaluated top down. 333 = 3(33) = 327
Using tiles of size 4x6 and 5x7, how would you tile a floor of size 1999x1999? The tiles cannot overlap and there can be no gaps.
Let Tn(x) be a sequence such that T1(x) = x and Tn+1(x) = xTn(x). For example,
T1(x) = x T2(x) = xx T3(x) = x(xx)For what positive values of x does limn→∞ Tn(x) converge?
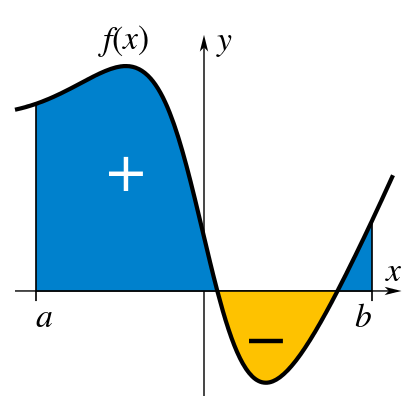
f(x) is a continuous function and f(x) >= 0 for all x. If
∫-∞∞ f(x) dx
is finite, does it follow that
∫-∞∞ [f(x)]2 dx
is finite?
 |
|---|