Quantum Relativistic Strong Planck Example
phenomena speeds gravity energy
Classical physics No No No No Rugby
Special relativity No Yes No No Interstellar spaceships
General relativity No Yes Yes No Black holes
Quantum mechanics Yes No No No Atomic sizes & smaller
Quantum field theory (QFT) Yes Yes No No Particle colliders
Quantum gravity Yes Yes Yes Yes Big bang
Quantum mechanics is relevant if the scale is equal to or less than the quantum
wavelength. If an object is larger than the quantum wavelength it behaves
classically.
In atoms, the size scale is small enough for quantum phenomena and the
characteristic speeds of electrons are nonrelativistic, and so this is the regime
of "Quantum mechanics".
In Ancient Greece, Aristarchus (310 BCE - 230 BCE) used a lunar eclipse to measure the size of the moon relative to the size of the Earth. He found that
Size of moon / Size of Earth ~ 1/3
Using this plus Eratosthenes' measurement of the size of the Earth, Aristarchus calculated that the distance to the moon is ~ 60 Earth radii.
Aristarchus also used a half moon to measure the distance to the sun and found that
Distance to sun / Distance to moon > 20
The true value, unmeasurable at the time, is
Distance to sun / Distance to moon = 420A solar eclipse tells us that the sun and moon have the same angular size.
Sun diameter = Moon diameter * Distance to sun / Distance to moonUsing this, Aristarchus established that the minimum size for the sun is
Sun diameter > 1/3 Earth diameters * 20
> 7 Earth diameters
This established that the sun is larger than the Earth, and this was the first solid
clue for heliocentrism. The true solar distance is
The measurement of the distance to the sun was refined by Aryabhata (476 CE - 550 CE).
If the Earth is stationary and if the sun orbits the Earth, then the stars will have zero parallax. If the Earth orbits the sun then the stars will have positive parallax. The parallax of stars is positive but it's too small for the eye to see. To the Ancient Greeks, this implied that either:
(*) The universe is Geocentric even though the sun is vastly larger than the Earth
or
(*) The universe is heliocentric and the stars must be extremely distant.
The resolution of the human eye is 3e-4 radians. Given that the parallax of stars is undetectable to the eye,
Z = Distance to the stars / distance to the sun > 2 / 3e-4 > 6700 Astronaumical units > .11 Light yearsIn 1831 Bessel produced the first successful measurement of a stellar parallax. He measured the distance to 61 Cygni to be 10.3 light years and the modern value is 11.4. The closest star is Proxima Centauri with a distance of 4.3 light years.
The fact that the stars are distant implies that they are luminous.
D = Distance to a star
Luminosity = Power radiated by a star in Watts.
Flux = Observed intensity of light from a star in Watts/meter^2.
= Luminosity / (4 Pi D^2)
Distance Luminosity Flux
from Earth (Watts) (Watts/m^2)
(ly)
Full Earth 5.4e16
Full Moon 4.1e-8 4.8e15 2.6e-3
Sun .000016 3.8e26 1360
Alpha Centauri A 4.36 5.9e26 2.7e-8
Sirius 8.58 9.8e27 1.2e-7
The brightest star is Sirius. If Sirius were at a distance of .11 light years
its luminosity would be .0043 solar luminosities, which is 340 million times
more luminous than the full moon. According to heliocentrism this is the
minimum luminosity for stars. This might have been hard for the Ancient Greeks
to accept.
In classical physics, an accelerating charge emits synchrotron photons and loses energy. If an electron orbits a proton then the emitted photons cause the electron to inspiral into the proton in 10^-15 seconds. This is an example where a theory predicts a phenomenon that breaks the theory, and this usually points the way to a more fundamental theory. The thing that stops the electron from crashing into the proton is quantum mechanics.
Suppose an electron is on a circular orbit around a proton.
R = Distance between the electron and the proton V = Velocity of the electron C = Speed of light = 3.00e8 m/s M = Electron rest mass = 5.68e-31 kg Z = Electric charge on an electron = 1.602e-19 Coulombs K = Electric force constant = 8.988*10^9 Newton Meter^2 / Coulomb^2 F = Force between the proton and electron = -K Z^2 / R^2 E = Electron kinetic energy = .5 M V^2 Ee = Electric energy between the proton and electron = Integral (Force dR) = -K Z^2 / R Q = Electron momentum = M V h = Planck Constant = 6.62 * 10-34 Joule seconds W = Electron quantum-mechanical wavelength = h / QBalance the electric and the centripetal forces:
K Z^2 / R^2 = M V^2 / RThe kinetic energy is
E = .5 M V^2 = .5 K Z^2 / RThe electron becomes relativistic when E ~ M C^2. Define
R_classical = Classical radius of the electron
= Radius of a circular orbit for which the kinetic energy equals the rest energy
= K Z^2 / (M C^2)
= 2.818e-15 meters
If R < R_classical, classical physics is guaranteed to fail and so some new
physics has to appear. A similar example is a black
hole where Newtonian gravity breaks down and general relativity takes over.
The Schwarzschild radius of a black hole is the characteristic distance where infalling matter becomes relativistic.
M = Mass of an electron
M_hole = Mass of a black hole
E_grav = - G M_hole M / R^2
R = Distance of an electron from a black hole
R_schwarz= Schwarzschild radius of a black hole, the closest distance from which
light can escape.
= 2 G M / C^2
Setting the gravitational energy equal to the rest energy gives the gravitational
radius of a black hole, which is proportional to the Schwarzschild radius.
As R->0, the scale where quantum mechanics becomes important is the "quantum radius of the electron".
To derive this scale we calculate the electron wavelength as a function of R. We assume that the electron is nonrelativistic and we assume the electron is on a circular orbit around the proton. The balance of electric and centripetal force is
W = Quantum-mechanical wavelength of the electrom R = Orbital radius of the electronThe parameter that characterizes the importance of quantum mechanics is W/R.
If W/R > 1 Quantum mechanics is important
If W/R < 1 Quantum mechanics is unimportant and classical physics can be used
W/R = (h/Q) * Q^2 / (K q^2 m)
= h Q / (K q^2 m)
= Constant * R^(-1/2)
As R-> Infinity W/R -> 0 Classical physics applies
As R-> 0 W/R -> Infinity Quantum mechanics applies
The radius where W/R=1 is the quantum radius of the electron.
R_quantum = h^2 / (K q^2 m)
= 2.086e-9 meters
We can compare the quantum radius to the classical radius.
R_quantum / R_classical = h^2 C^2 / (K^2 q^4)
= 740000
Because R_quantum / R_classical >> 1, quantum mechanics becomes important
before relativity.
R_quantum sets the size of atoms. If you calculate the electron orbital radius
in a hydrogen atom using the Bohr theory,
R_bohr = R_quantum / (2 Pi)
= 5.29e-11 meters
This is the radius of the S=1 orbital in a hydrogen atom.
If a particle is nonrelativistic (V << C),
Q = Momentum = m V E = Energy = .5 m V^2 Q^2 = 2 m EIf a particle is relativistic (V~C),
E ~ Q CFor relativistic particles we can define an equivalence between space and time by setting V=C.
Space = C * TimeWe can also define an equivalence between space and energy by setting the space scale equal to the quantum mechanical wavelength.
E = Q C = h C / WIf we set E equal to the particle's rest energy, we call the resulting wavelength the "Compton wavelength". This particle is "barely relativistic".
m C^2 = h C / R_compton R_compton = h / (m C)All particles with finite mass have a Compton wavelength.
If a photon has the same energy as a particle's rest energy the wavelength of the photon is equal to the Compton wavelength.
For an electron,
R_compton = 2.426e-12 meters
We can define a measure of the strength of the electric force "Z" by using photons. Suppose two electrons are a distance R apart and a photon has wavelength W = 2 Pi R. The photon energy is E = hf = hC/W.
Z = Electric energy / Photon energy = (K q^2 / R) / (hC/W) = 2 Pi K q^2 / (hC) = .007297Z is the "Fine structure constant", an important dimensionless number that appears everywhere in physics. For example,
R_classical / R_compton = Z / (2Pi) R_classical / R_quantum = Z^2 / (2Pi)^2 Electron charge / Planck charge = Z^(1/2)
Force Force carrying Mass of force Compton radius of
particle carrying particle force-carrying particle
(GeV) (meters)
Gravity Graviton 0 Infinite
Weak W 80 1.5e-17
Z 91 1.4e-17
Electromagnetic Photon 0 Infinite
Strong Pion .135 9.2e-15
Technically the strong force is carried by gluons.
For protons and neutrons in a nucleus the strong force can be considered to be
carried by pions.
If a force is carried by a massless particle then the force is given by Force = Constant / R^2 such a force is said to have "infinite range".
If the force is carried by a massive particle then the force is said to have "finite range". The range of the force is equal to the carrier's Compton wavelength and beyond this range the force is essentially zero.
The size scale of the nucleus is determined by the pion's Compton wavelength.
The force carrying particles for the weak force are heavy and hence the weak force has short range, 100 times shorter than the size of a nucleus. This is why the weak force is weak.
The fine structure constant characterizes the strength of the electromagnetic force.
For two electrons, the gravitational force is vastly weaker than the electric force.
Force of gravity / Electric force = G m^2 / K q^2 = 2.40e-43
Quantum mechanics resolved the electron crisis. The next crisis is the Higgs crisis.
Higgs mass = 125.3 GeV
meters
Electron quantum radius 2.09e-9 Limit for classical physics
Atomic scale 2e-10
Electron Compton radius 2.43e-12 Limit for non-relativistic quantum mechanics
Electron classical radius 2.82e-15
Nuclear scale 1e-15
Higgs Compton radius 9.9e-18
Suppose we consider a length scale R.
If R > Electric quantum radius Classical physics applies If R < Electron quantum radius Quantum mechanics apples If R > Electron Compton radius Non-relativistic quantum mechanics may be used If R < Electron Compton radius Relativistic quantum mechanics must be used If R > Higgs Compton radius The Standard Model applies If R < Higgs Compton radius The Standard Model breaks downThe Standard Model breaks down for scales below the Higgs scale and some new theory must take over for smaller scales. The most promising candidates are "Supersymmetry" and "The Multiverse". The Large Hadron Collider can at present explore down to the Higgs scale but no further. When it is upgraded to higher energies in 2015 it will be able to go beyond the Higgs scale.
There is much drama in the world of supersymmetry. It is predicted that the LHC should already have detected supersymmetric particles and thus far none have been found.
Tangible matter = Stuff that interacts by the strong and/or electromagnetic force,
such as protons, neutrons, electrons, photons.
These particles can be stopped by a meter of lead.
Dark matter = Stuff that does not interact by the strong or electromagnetic
force but interacts by the weak force and gravity.
These particles easily pass through the Earth.
Examples include neutrinos.
Most of the dark matter in the universe consists of particles
that have not yet been discovered.
Dark energy = An energy density that has negative pressure.
Tangible matter and dark matter have positive pressure and dark energy has negative
pressure. All three have positive energy density.
Densities:
kg/m^3
Planck density 5 *10^96 = PlanckMass / PlanckLength^3
Black hole 1.8 *10^19 = Density of a 1 solar mass black hole
Neutron star 1 *10^18 = Upper range for the density at the core
Nuclear matter 2.3 *10^17 = Density of a nucleus
White dwarf 1 *10^9 = White dwarf density
Osmium 22.6 *10^3 = Densest element
Water 1 *10^3
Solar system 2 *10^-8 = Mass of sun / (30 AU)^3
Milky Way 3 *10^-21 = 1.2e12 solar masses / (100000 lightyears)^3
Ordinary matter .12*10^-27 = Mean density of protons, neutrons, & electrons in the universe
Dark matter .66*10^-27 = Mean density of dark matter in the universe
Dark energy 1.67*10^-27 = Mean density of dark energy in the universe
Sum 2.45*10^-27 = Total density of matter, dark matter, and dark energy
As the universe expands the matter and dark matter density decrease and the
dark energy density is constant.
In the early universe the dark matter density was vastly greater than the dark energy density. In the future dark energy will overwhelm dark matter and the universe will expand unchecked.
The Earth's escape velocity is Ve=11.2 km/s. Suppose the Earth had no atmosphere and you launched a cannonball upward with velocity V.
Trajectory
V < Ve Elliptic The cannonball falls back to the Earth
V > Ve Hyperbolic The cannonball escapes from the Earth and asymptotes to a
positive velocity
V = Ve Parabolic The cannonball is on the boundary between escape and falling back. It never returns to the Earth and it asymptotes to zero velocity.
If the universe consisted entirely of ordinary matter and dark matter and no
dark energy, then there is a critical value of the density such that the
expansion of the universe is parabolic. This value is 2.45e-27 kg/m^3.
d = Density of a parabolic universe = 2.45e-27 kg/m^3 D = 1.0 = Density of all matter and dark energy in the universe / d Dom = .049 = Fraction of ordinary matter in the universe / d Ddm = .27 = Fraction of dark matter in the universe / d Dde = .68 = Fraction of dark energy in the universe / dD, Dom, Ddm, and Dde are scaled relative to the parabolic density d.
If Dde = 0 then
If D > 1 The density of the universe is large enough to reverse the expansion from
the big bang and the universe collapses in a Big Crunch.
The Hubble constant goes from positive to zero to negative.
If D > 1 The universe expands forever, ending with a positive Hubble constant
If D = 1 The universe stops expanding and the Hubble constant goes to zero.
The universe ends in a "Big Chill".
If Dde > 0 then dark energy trumps all of the above. If the universe survives long
enough to avoid a Big Crunch then dark energy causes the universe to expand unchecked
regardless of the matter density. The universe ends in a Big Chill.
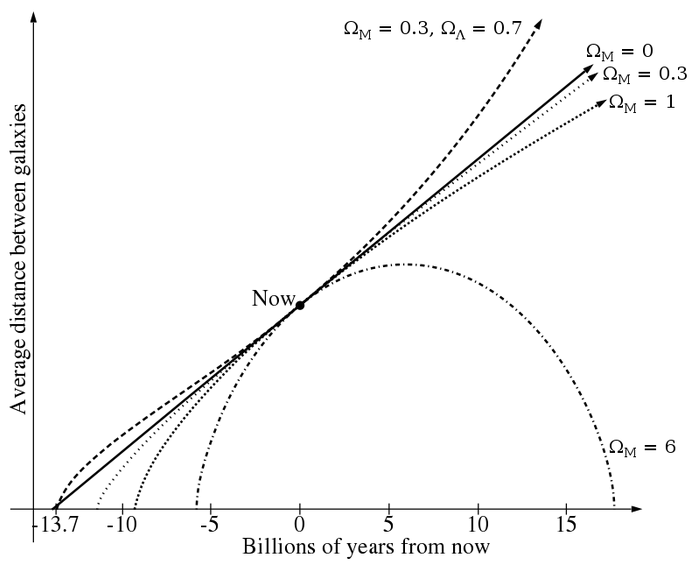
Previous to 2005 we knew that the value of D was close to 1 and we couldn't tell if it was larger or smaller than 1. The value of the dark energy density was unknown and the fate of the universe was unknown. The theory of "Inflation" was developed to explain why D is close to 1.
In 2005 measurements of distant supernovae showed that Dde > 0, implying that the universe will end in a Big Chill.
In 2010 the Planck spacecraft measured the precise values of Dom, Ddm, and Dde.
In the plot, Omega_M = Dom + Ddm Omega_Lambda = Dde
 |
|---|
You can illustrate the concept of escape velocity with the "My Solar System" simulation at phet.colorado.edu.
Mass Position Velocity
X Y X Y
Body 1 100. 0 0 0 0 Sun
Body 2 1. 100 0 Vx Vy Planet
If Vx=100 and Vy=0 the planet orbits the sun on a circular orbit.
What do the orbits look like if you vary Vx?
The escape velocity from the sun at X=100 is Ve=100*Squareroot(2).
If Vx=0 and Vy > Ve the planet escapes. If Vx=0 and Vy < Ve the planet crashes into the sun.
1635 Gassendi measures the speed of sound to be 478 m/s with 25% error.
1660 Viviani and Borelli produce the first accurate measurement of the speed of
sound, giving a value of 350 m/s.
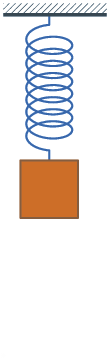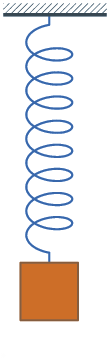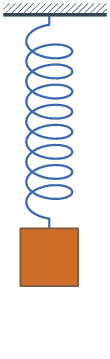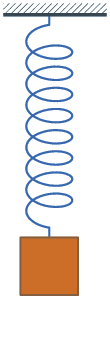
1660 Hooke's law published. The force on a spring is proportional to the change
in length.
1662 Boyle discovers that for air at fixed temperature,
Pressure * Volume = Constant
1687 Newton publishes the Principia Mathematica, which contains the first analytic
calculation of the speed of sound. The calculated value was 290 m/s.
The fact that Newton's calculation differed from the measured speed was the first
solid clue for the existence of atoms, and it also contained a clue for quantum
mechanics.
 |
 |
 |
|---|---|---|
Because of Hooke's law, springs oscillate with a constant frequency.
X = Displacement of a spring V = Velocity of the spring A = Acceleration of the spring F = Force on the spring M = Spring mass Q = Spring constant q = (K/M)^(1/2) t = time T = Spring oscillation periodHooke's law and Newton's law:
F = - Q X = M A A = - (Q/M) X = - q^2 XThis equation is solved with
X = sin(q t) V = q cos(q t) A = -q^2 sin(q t) = - q^2 XThe oscillation period of the spring is
T = 2 Pi / q = 2 Pi (M/Q)^(1/2)According to Boyle's law, a gas functions like a spring and hence a gas oscillates like a spring. An oscillation in a gas is a sound wave.
For a gas,
P = Pressure dP = Change in pressure Vol = Volume dVol= Change in volumeIf you change the volume of a gas according to Boyle's law,
P Vol = Constant P dVol + Vol dP = 0 dP = - (P/Vol) dVolThe change in pressure is proportional to the change in volume. This is equivalent to Hooke's law, where pressure takes the role of force and the change in volume takes the role of displacement of the spring. This is the mechanism behind sound waves.
In Boyle's law, the change in volume is assumed to be slow so the gas has time to equilibrate with its surroundings. In this case the the temperature is constant as the volume changes and the change is "isothermal".
P Vol = ConstantIf the change in volume is fast then the walls do work on the molecules, changing their temperature. If there isn't enough time to equilibrate temperature with the surroundings then the change is "adiabatic". You can see this in action with the "Gas" simulation at phet.colorado.edu.
In Newton's time it was not known that a a change in volume produces a change in temperature.
If a gas consists of pointlike particles then
Vol = Volume of the gas
Ek = Total kinetic energy of gas molecules within the volume
E = Total energy of gas molecules within the volume
= Kinetic energy plus the energy from molecular rotation and vibration
dE = Change in energy as the volume changes
P = Pressure
dP = Change in pressure as the volume changes
D = Density
C = Speed of sound in the gas
d = Number of degrees of freedom of a gas molecule
= 3 for a monotomic gas such as Helium
= 5 for a diatomic gas such as nitrogen
G = Adiabatic constant
= 1 + 2/d
= 5/3 for a monatomic gas
= 7/5 for a diatomic gas
k = Boltzmann constant
T = Temperature
The ideal gas law is
P Vol = (2/3) Ek (Derived in www.jaymaron.com/oom/gas.html)This law is equivalent to the formula that appears in chemistry: P Vol = Moles R T but the above form is more useful.
For a gas in thermal equilibrium each degree of freedom has a mean energy of .5 k T. For a gas of pointlike particles (monotomic) there are three degrees of freedom, one each for motion in the X, Y, and Z direction. In this case d=3. The mean kinetic energy of each gas molecule is 3 * (.5 k T). The total mean energy of each gas molecule is also 3 * (.5 k T).
For a diatomic gas there are also two rotational degrees of freedom. In this case d=5.
In general,
Ek = 3 * (.5 k T) E = d * (.5 k T) Ek = (3/d) EIf you change the volume of a gas adiabatically, the walls change the kinetic and rotational energy of the gas molecules.
dE = -P dVolThe ideal gas law in terms of E instead of Ek is
P Vol = (2/d) E
dP = (2/d) (dE/Vol - E dVol/Vol^2)
= (2/d) [-P dVol/Vol - (d/2) P dVol/Vol]
= -(1+2/d) P dVol/Vol
= - G P dVol/Vol
This equation determines the speed of sound in a gas.
C^2 = G P / DFor air,
P = 1.01e5 Newtons/meter^2 D = 1.2 kg/meter^3Newton assumed G=1 from Boyle's law and calculated the speed of sound in air to be
C = 290 m/sThe correct value for air is G=7/5, which gives a sound speed of
C = 343 m/swhich is in accord with the measurement.
For a gas, G can be measured by measuring the sound speed. The results are
Helium 5/3 Monatomic molecule Argon 5/3 Monatonic molecule Air 7/5 Oxygen 7/5 Diatomic molecule Nitrogen 7/5 diatomic moleculeThe fact that G is not equal to 1 was the first solid evidence for the existence of atoms and it also contained a clue for quantum mechanics. If a gas is a continuum it has G=1 and if it consists of pointlike particles (monatonic) it has G=5/3. This explains helium and argon but not nitrogen and oxygen. Once it was discovered that nitrogen and oxygen are diatomic the crisis was still not resolved because G=4/3 for a diatomic molecule. The reason G=7/5 instead of 4/3 is because quantum mechanics freezes out one of the rotational degrees of freedom of the diatomic molecule so that d=5 instead of d=6.
For dark energy,
E = Energy dE = Change in energy e = Energy density Vol= Volume P = PressureThe volume expands as the universe expands.
As a substance expands it does work on its surroundings according to its pressure.
dE = - P dVolFor dark energy, the energy density "e" is constant in space and so
dE = e dVolHence,
P = - eDark energy has a negative pressure, which means that it behaves differently from a continuum and from particles.
Dark matter consists of pointlike particles and has a particle-like pressure with G=5/3.
Scale Constituents of matter (meters) 1 Materials, gases, chemicals, pizza 10^-9 Molecules 10^-10 Elements (hydrogen, helium, ...) 10^-14 Nuclei & electrons 10^-15 Protons, neutrons, pions, electrons, photons, neutrinos, dark matter 10^-16 Quarks, electrons, photons, gluons, neutrinos, W, Z, Higgs, dark matter
Parameters of the universe:
Number of Parameter
parameters
6 Quark masses. Up, down, charm, strange, top, bottom
3 Lepton masses. Electron, muon, tau
3 Neutrino masses. Electron neutrino, muon neutrino, tau neutrino
1 Z mass. The W mass is determined by the Z mass.
1 Higgs mass
1 Electric force constant
1 Gravitational force constant
1 Strong force constant
1 Weak force constant
4 3 Neutrino mixing angles and one phase
6 Cosmological parameters. These are:
Density of tangible matter in the universe (nuclei, electrons, etc)
Density of dark matter in the universe
Dark energy density (cosmological constant)
Scalar spectral index of the universe
Curvature fluctuation amplitude of the universe
reionization optical depth of the universe
Dark matter is likely a source of new parameters, such as the masses of the dark
matter particles.
The masses of the proton and neutron can be calculated from the masses of the up and down quark.
At present the origin of these parameters is unknown. Ideally, a future physics theory will explain the origin of the parameters based on a compact set of principles, and the number of parameters will decrease. This was the hope of Einstein. Since special relativity and general relativity can be generated from compact principles it was hoped that particle physics could as well, but at present no successful principles have been found.
An alternative to principles is The Multiverse, where there are multiple universes, each with different parameters, and we live in a universe where the parameters allow for the existence of intelligent life. This is similar to the Anthropic Principle.
If you change the parameters of the universe there are extreme consequences. For example,
If the electron mass increases, protons will consume the electrons to produce neutrons, leaving behind a boring universe with no nuclei.
If the dark energy density is increased, the universe expands too fast for galaxies to form.
If you increase the electric force relative to the strong force then nuclei can't form.
Possibilities for the laws of physics:
Natural The parameters of the universe will be found to originate
from compact principles and no fine tuning is required for life.
Fine tuned The parameters of physics require fine tuning to be
amenable to life.
Intelligent design The parameters of the universe were designed to be amenable
to life.
Multiverse There are multiple universes with different laws of physics,
most of them dull and lifeless, but the probability of one of
them accomodating life is unity.
Fortuitous There is only one universe. The laws of physics require fine
tuning and we are lucky that they are amenable to life.
Matrix The universe is a computer simulation.
Darwin universe Universes beget universes and the laws of physics evolve
by natural selection.
An analogue of The Multiverse is the Drake equation.
P = Probability that a star has a planet with intelligent life
N = Number of stars in the universe.
If:
P ~ 1 Life is natural
P << 1 Life requires fine tuning
P << 1 and PN >> 1 Life requires fine tuning but life is probable in the universe.
This is the "Anthropic principle" or the "Multiverse" scenario.
P << 1 and PN << 1 Life is improbable in the universe.
Either life is "Lucky" or we live in The Matrix or the
Earth was intelligently designed.
Mass of orbiting objects /
Mass of central object
Sun .00134
Mercury 0
Venus 0
Earth .0123
Mars .000000004
Jupiter .00021
Saturn .000239
Uranus .000070
Neptune .00021
Pluto .12 Moon = Charon
Eris .0048 Moon = Dysnomia
Orcus .069 Moon = Vanth
For the sun, the value given is for the mass of the planets divided by the
mass of the sun.
The planets formed within the sun's accretion disk, and the moons of the gas giants formed within the gas giant's accretion disk. The Earth's moon and Charon were likely formed by collisions.
If two planets collide, most of the material ends up in the merged planet and some of it is ejected into orbit where it forms a ring. Any material within the Roche radius falls back to the planet and any material beyond the Roche radius coalesces into a moon. The moon subsequently spirals outward from the Roche radius due to the planet-moon tidal interaction. In this scenario, the planet is always much more massive than the moon.
Mass of moon / Mass of Earth = .0123This is a "natural" result because we expect the moon to be less massive.
Suppose instead that
Mass of moon / Mass of Earth = 1.00000000045571This is not forbidden by the laws of physics but it is unlikely. One has to construct a "fine tuned" scenario to make this happen. Alternatively, the Earth and moon could have been designed by aliens.
Mount Fuji: Natural Stonehenge: Intelligent design
1789 Lavoisier finds that combustion conserves mass
1789 Lavoisier publishes the "Elementary Treatise of Chemistry", the
first modern textbook.
He lists a set of irreducible substances, which were
oxygen, nitrogen, hydrogen, phosphorus, mercury, zinc, and sulfur.
1808 Dalton publishes the law that elements combine in integer ratios.
1828 Berzelius publishes a list of the atomic weights of all known elements.
Among the elements known in 1828, the ones that are lighter than iron are:
Mass Protons Discovery
Hydrogen 1.0000 1 1766
Lithium 6.88 3 1821
Boron 10.725 5 1808
Carbon 11.916 6 Ancient
Nitrogen 13.897 7 1772
Oxygen 15.873 8 1771
Sodium 22.809 11 1807
Magnesium 24.114 12 1755
Aluminum 26.769 13 1825
Silicon 27.864 14 1824
Phosphorus 30.730 15 1669
Sulfur 31.807 16 Ancient
Chlorine 35.171 17 1774
Potassium 38.790 19 1807
Calcium 39.762 20 1808
Chromium 51.586 24 1797
Manganese 54.505 25 1774
Iron 55.405 26 -1200
Masses have been normalized to the hydrogen mass. At the time it was not
obvious if the elements were composed of more fundamental particles. This was
because not all of the elements were known, and also because an element can
consist of a mixture of isotopes, clouding the mass.