
 |
|---|
Section 1: Physics of music (this section)
Section 2: Materials and elasticity
Section 3: Anatomy
Section 4: Music performance
Section 5: Physics
Balance
History of kung fu
Instrument balance
![]() Sword
Angular momentum
Frames of reference
Speed
Eyes
Damage control
Fundamentals
Phase lock
Standard violin technique
Videos
Styles
Sword
Angular momentum
Frames of reference
Speed
Eyes
Damage control
Fundamentals
Phase lock
Standard violin technique
Videos
Styles
Units Conservation of momentum and energy Angular momentum
 |
 |
|---|---|
 |
 |
|---|---|
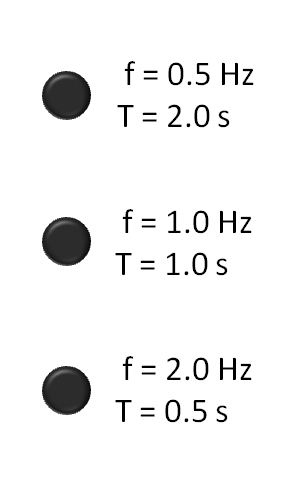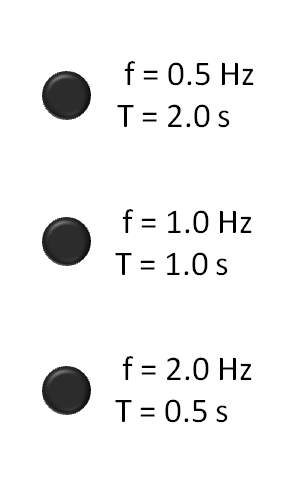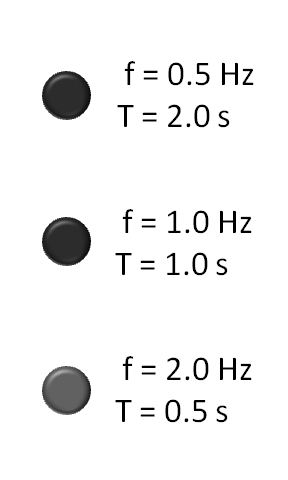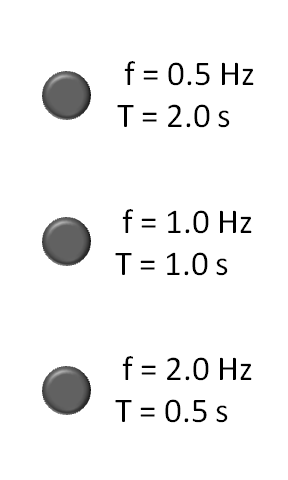 |
|---|
The properties of a wave are
F = Frequency (1/seconds) W = Wavelength (meters) V = Wavespeed (meters/second) T = Period (seconds) (The time it takes for one wavelength to pass by) A = Amplitude (half the distance between the top and bottom crests of the wave)Wave equations:
F W = V F T = 1
 |
|---|
Length of a train car = Wavelength = W = 10 meters Speed of the train = Wavespeed = V = 20 meters/second Cars per second = Frequency = F = 2 Hertz Car time = Period = T = .5 seconds
 |
|---|
Speed of sound at sea level = V = 340 meters/second Frequency of a violin A string = F = 440 Hertz Wavelength of a sound wave = W = .77 meters = W/F Wave period = T = .0023 seconds
 |
|---|
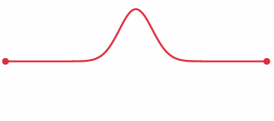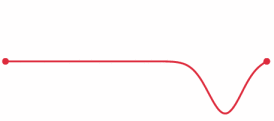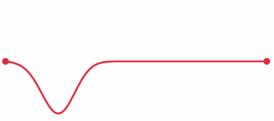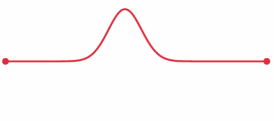
A wave on a string moves at constant speed and reflects at the boundaries.
Frequency of a violin A-string = F = 440 Hertz Length of a violin A-string = L = .32 meters Round trip time up and down the string = T = 2L/V = F-1 =.00227 seconds Speed of a wave on a violin A-string = V = F/(2L) = 688 meters/second
 |
|---|
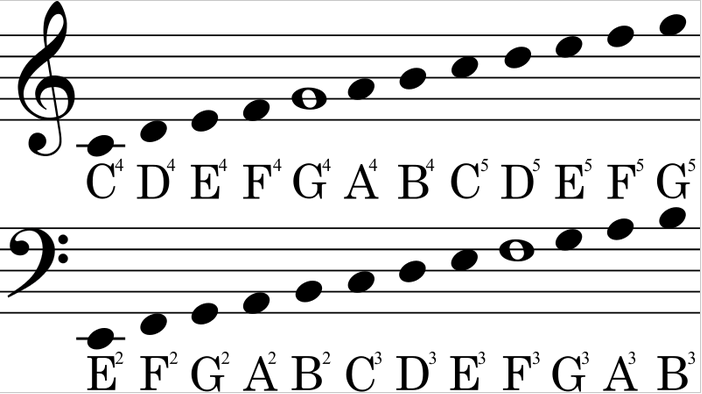
The "A" at the center of the treble clef has a frequency of 440 Hertz. We will use this "A" as a reference. There are 12 notes between this "A" and the "A" an octave above it, where each note is separated by a half step.
Note Note Notes in an Notes in an Name of index letters A-major scale A-minor scale interval 0 A A A Tonic 1 A# or Bb Minor second = Half step 2 B B B Major second = Whole step 3 C C Minor third 4 C# or Db C# Major third 5 D D D Perfect fourth 6 D# or Eb Tritone 7 E E E Minor fifth 8 F F Minor sixth 9 F# or Gb F# Major sixth 10 G G Minor seventh 11 G# or Ab G# Major seventh 12 A A A Octave"A#" stands for "A sharp" and "Bb" stands for "B flat".
The bottom note is the "tonic" and the "interval" is the distance between the tonic and the given note.
When describing intervals we will usually refer to the note index rather than the interval name or the note letter. A change of index of 1 is a half step and a change of index of 2 is a whole step. An octave is 12 half steps.
 |
 |
|---|---|
The choice of "A" for the tonic is arbitrary. We could have used any of the other 11 notes. If the tonic is "D" then the notes in a major and minor scale are:
 |
 |
|---|---|
A chromatic scale contains all 12 notes. A chromatic scale with a tonic of "C" looks like:
 |
|---|
Wikipedia: Clefs Musical intervals Chromatic scale Major scale Minor scale Octave Perfect fifth Perfect fourth
If two notes are played at the same time then we hear the sum of the waveforms.
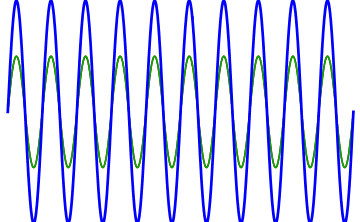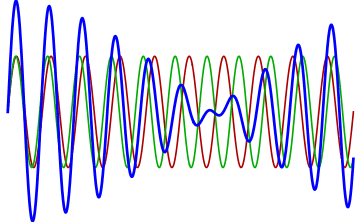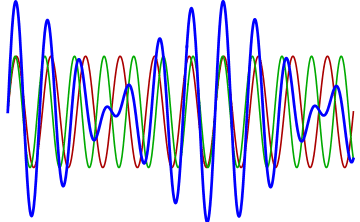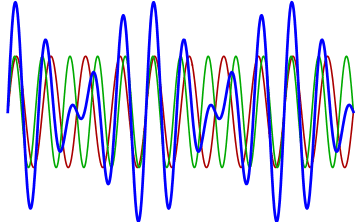
If two notes are played such that the frequency of the high note is twice that of the low note then this is an octave. The wavelength of the high note is half that of the low note.
Color Frequency Wavelength Orange 220 Hertz 1 Red 440 Hertz 1/2Because the red and orange waves match up after a distance of 1 the blue note is periodic. This makes it easy for your ear to process.
 |
|---|
If we double both frequencies then it also sounds like an octave. The shape of the blue wave is preserved.
 |
|---|
Color Frequency Wavelength Orange 440 Hertz 1/2 Red 880 Hertz 1/4When listening to two simultaneous pitches our ear is sensitive to the frequency ratio. For both of the above octaves the ratio of the high frequency to the low frequency is 2.
440 / 220 = 2 880 / 440 = 2If we are talking about frequency ratios and not absolute frequencies then for simplicity we can set the bottom frequency equal to 1. Hence for an octave,
F1 = 1 F2 = 2For a fifth (playing an A and an E),
F1 = 1 F2 = 3/2
 |
|---|
 |
|---|
 |
|---|
 |
|---|
 |
|---|
 |
|---|
The octave, fifth, fourth, major third, and minor third are all periodic and sound harmonious.
The tritone is not periodic and sounds dissonant.
If two notes in an interval have frequencies such that
Frequency of top note / Frequency of bottom note = I / J where I and J are small integersthen the summed note will be periodic. The smaller the integers I and J, the more noticeable the periodicity and the more harmonious the interval. This is why fifths and fourths sound more resonant than thirds.
If the note "A" is played together with the notes of the 12-tone scale the result is
Note Interval Frequency Result A Unison 1.000 Strongly resonant Bb Minor second 1.059 Dissonant B Major second 9/8 Resonance barely noticeable C Minor third 6/5 Weakly resonant C# Major third 5/4 Weakly resonant D Fourth 4/3 Strongly resonant Eb Tritone 1.414 Dissonant E Fifth 3/2 Strongly resonant F Minor sixth 1.587 Weakly resonant F# Major sixth 5/3 Weakly resonant G Minor seventh 1.587 Dissonant G# Major seventh 1.888 Dissonant A Octave 2 Strongly resonantThe notes {Bb, B, Eb, G, Ab} cannot be expressed as a ratio of small integers and so they sound dissonant when played together with an A.
If two notes are out of tune they produce dissonant beat frequencies.
Frequency of note #1 = F1 Frequency of note #2 = F2 Beat frequency = Fb = F2 - F1For the beats to not be noticeable, Fb has to be less than one Hertz. On the E string there is little margin for error. Vibrato is often used to cover up the beat frequencies.
 |
|---|
 |
|---|
 |
|---|
 |
|---|
The more out of tune the note, the more pronounced the beat frequencies. In the first figure, the notes are in tune and no beat frequencies are produced.
If you play an octave out of tune you also get beat frequencies.
 |
|---|
 |
|---|
 |
|---|
If you want to divide the octave into 12 pitches such that the interval between each pitch is equal, the pitches have the form
I = An integer where 0 corresponds to the tonic and 12 corresponds to the octave. F = Frequency of the pitches = 2I/12For the tonic,
F = 20/12 = 1For the octave,
F = 212/12 = 2The frequency ratio between two adjacent pitches is
Frequency ratio = 2(I+1)/12 / 2I/12
= 21/12
= 1.059
which is independent of I.
 |
|---|
Note Index Interval Equal Just tuning Major Minor Pythagorean Cents
tuning scale scale tuning
A 0 Unison 1.000 1.000 = 1/1 * * 1/1 = 1.000 0
Bflat 1 Minor second 1.059 256/243 = 1.053
B 2 Major second 1.122 1.125 = 9/8 * * 9/8 = 1.125 + 9
C 3 Minor third 1.189 1.200 = 6/5 * 32/27 = 1.185 -16
C# 4 Major third 1.260 1.250 = 5/4 * 81/64 = 1.266 +14
D 5 Fourth 1.335 1.333 = 4/3 * * 4/3 = 1.333 + 2
Eflat 6 Tritone 1.414 729/512 = 1.424
E 7 Fifth 1.498 1.500 = 3/2 * * 3/2 = 1.500 - 2
F 8 Minor sixth 1.587 1.600 = 8/5 * 128/81 = 1.580 -14
F# 9 Sixth 1.682 1.667 = 5/3 * 27/16 = 1.688 +16
G 10 Minor seventh 1.782 * 16/9 = 1.778
Aflat 11 Major seventh 1.888 * 243/128 = 1.898
A 12 Octave 2.000 2.000 = 2/1 * * 2/1 = 2.000 0
In equal tuning, the frequency ratio of an interval is
Frequency ratio = 2(Index/12) Where "Index" is an integerEqual tuning is based on equal frequency ratios. Just tuning adjusts the frequencies to correspond to the nearest convenient integer ratio. For example, in equal tuning, the frequency ratio of a fifth is 1.498 and just tuning changes it to 1.500 = 3/2.
For the 12 tone scale, equal tuning and just tuning are nearly identical.
The major and minor modes favor the resonant notes.
Cents refers to the difference between just tuning and equal tuning. 100 Cents corresponds to a half step and 1 cent corresponds to .01 half steps.