Mountains and the roundness of solar system objects






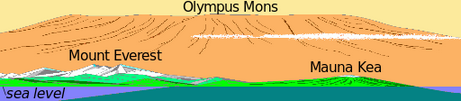
Olympus Mons and Hawaii
Ceres
Vesta




If a mountain gets too high, pressure causes the rock to deform elastically and
the mountain sags.  The height of a mountain is limited by the pressure that the
rock can withstand.  This critical pressure is called the "yield modulus".  For
a stout rock such as granite this is ~ 100 MegaPascals (Newton / meter^2).  The
density of granite is ~ 3000 kg/m^3.

The pressure at the base of a mountain is

Pressure = RockDensity * g * Height

The height that gives a pressure of 100 MegaPascals is

Height  ~  10^8 N/m^2   /  10 m/s^2  /  3000 kg/m^3  ~  3 km

       Gravity  Radius  Tallest mountain
       (m/s^2)   (km)     (km)
Earth    9.8     6371     10        Mount Everest
Mars     3.7     3386     21        Mount Olympus
Io       1.80    1822
Ceres     .27     476               Round
Moon     1.62    1738
Vesta     .25     265               Not round
Pluto     .66    1173

What would you predict is the maximum height of a mountain on Ceres?

If a planet is substantially heavier than the earth and if it has enough
water for oceans, gravity might make it impossible for dry land to exist.
http://en.wikipedia.org/wiki/olympus_mons


Round or potato?

If we define roundness of an object as the characteristic mountain height
divided by the object's radius, then for the Earth,

Roundness ~ 10 km / 7*10^3 km ~ 10^-3

If a mountain is too high, pressure deforms the rock and the mountain
sags. Pressure is proportional to gravity, and gravity for equal-density
objects is proportional to radius, hence the roundness of an object of
radius r scales as

Roundness  ~  10^-3 * (r / RadiusOfEarth)^2

For an object a tenth the size of the earth, the roundness is ~ 10^-1.
if we take this magnitude as the boundary between round and potato-shaped,
then the smallest round objects should be a tenth the Earth's radius.
The smallest round object in the solar system is Ceres, which has
a radius of 487 km. The radius of the earth is ~ 6370 km.