





 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|
 |
|---|
 |
|---|
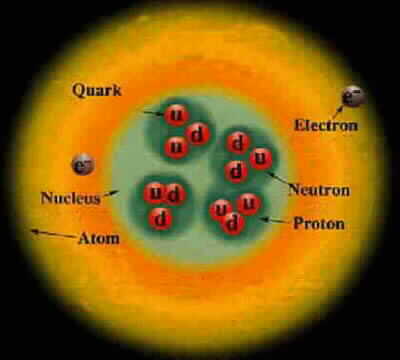
Atoms consist of the following particles:
Particle Symbol Charge Mass
(MeV)
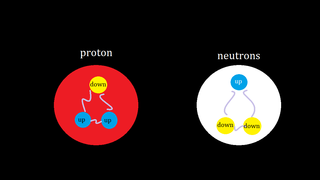
Proton p +1 938.3 p = u + u + d + gluons
Neutron n 0 939.6 n = u + d + d + gluons
Electron e- -1 .511
Up quark u +2/3 2.2
Down quark d -1/3 4.6
Photon γ 0 0 Carries the electromagnetic force and binds electrons to the nucleus
Gluon g 0 0 Carries the strong force and binds quarks, protons, and neutrons
 |
|---|
The only stable particles in the chart are electrons, up quarks, down quarks, and protons. All other particles decay.
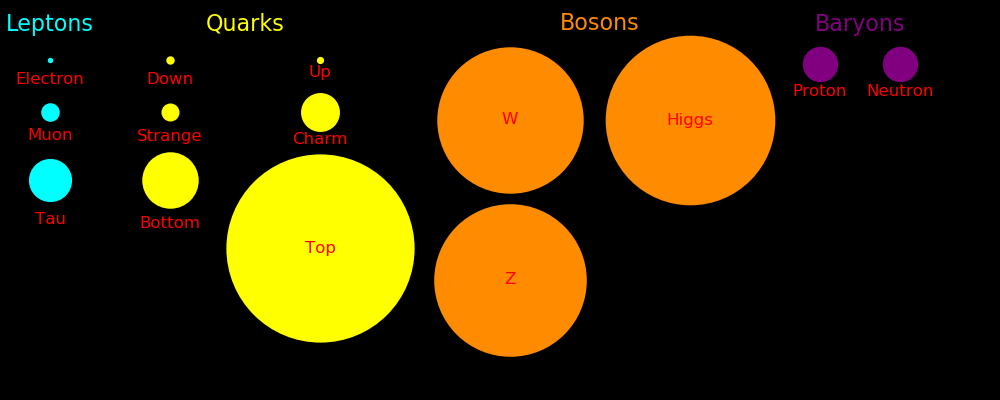
There are 6 quarks: Up, down, charm, strange, top, and bottom.
There are 6 leptons: Electron, muon, tauon, electron neutrino, mu neutrino, and tau neutrino.
The masses of neutrinos are unknown, but they're known to be positive.
Quarks are never found in isolation.
A "hadron" is composed of 3 quarks, such as protons and neutrons.
A "meson" is composed of 2 quarks, such as pions and kaons.
"Fermions" have spin 1/2 or 3/2, and these include quarks, leptons, and neutrinos.
"Bosons" have spin 0, 1, or 2, and these include photons, gravitons, gluons, the weak bosons, and the Higgs boson.
 |
|---|
Fermions don't interact directly. They always interact through a boson. Each force is associated with a boson. For example, photons are bosons, and they carry the force exerted by charged particles.
Each force is associated with boson, and also with a quantity. The quantity is ususally conserved, but not always. For example, the conserved quantity for the electric force is charge.l
Some bosons interact with other bosons and others don't. Photons don't interact with other photons because photons interact with electric charge, and photons don't have charge.
Gravitons interact with other gravitions because gravitons interact with energy, and gravitons have energy.
Gluons interact with other gluons because gluons interact with color charge, and gluons carry color charge.
Force Felt by Boson Relative Particles that interact with the boson
strength
Gravity Energy Graviton 10-40 All particles
Electric Charge Photon 1 All particles with charge, plus gravitons
Strong Color charge Gluon 100 Particles with color charge (quarks & gluons), plus gravitons
Weak W Weak isospin W+ 10-5 Quarks, leptons, Higgs, W-, Z, graviton, photon. All except gluons
Weak Z Weak charge Z 10-5 Quarks, leptons, Higgs, W-, Z, graviton. All except gluons and photons
Higgs Mass Higgs All particles with positive rest mass, plus gravitons
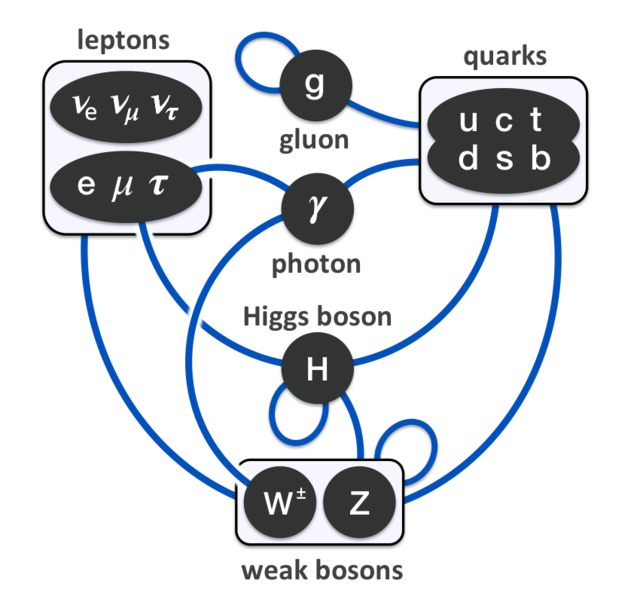 |
|---|
A blue line indicates that an interaction exists between the given particles. For example, an electron interacts with a photon. The Higgs interacts with all particles with positive rest mass.
The conserved quanties of physics are:
Energy Momentum Angular momentum Electric charge Color charge (3 types, all separately conserved) Weak charge (2 types, not separately conserved) Baryon number (number of quarks - number of antiquarks) Lepton number (number of leptons - number of antileptons)
"Baryon number" could be called "quark number". The total number of quarks minus antiquarks is conserved.
Weak charge and weak hypercharge are not conserved. A combination of them is conserved.
Every particle has an antiparticle. Some particles are identical to their antiparticle, those being the neutral bosons (Photon, gluon, Z, Higgs, graviton).
A particle and its antiparticle have opposite charge.
Symbol Charge Spin Rest mass Strong Lifetime Decay products
(GeV) force (seconds)
Up quark u +⅔ ½ .0022 * Stable
Charm quark c +⅔ ½ 1.25 * 1⋅10-12 s + e+ + νe
Top quark t +⅔ ½ 171 * 5⋅10-25 b + e+ + νe
Down quark d -⅓ ½ .0046 * Stable u + e- + νe
Strange quark s -⅓ ½ .1 * 1.2⋅10-8 u + e- + νe
Bottom quark b -⅓ ½ 4.2 * 1.6⋅10-12 c + e- + νe
Electron e- -1 ½ .000511 Stable
Muon μ- -1 ½ .1057 2.2⋅10-6 e- + νe + νμ
Tau τ- -1 ½ 1.777 2.9⋅10-13 π- + π0 + ντ
Electron neutrino νe 0 ½ <2.2e-9 Oscillates to muon neutrino or tau neutrino
Muon neutrino νμ 0 ½ <.00017 Oscillates to electron neutrino or tau neutrino
Tau neutrio ντ 0 ½ <.016 Oscillates to electron neutrino and muon neutrino
Photon γ 0 1 0 Stable
Gluon g 0 1 0 * Stable
Graviton G 0 2 0 * Stable Hypothetical
W boson W+ +1 1 80.4 3⋅10-25 e+ + νe
Z boson Z0 0 1 91.2 3⋅10-25 e+ + e-
Higgs Boson H0 0 0 125.3 1.6⋅10-22 b + b
Proton p +1 ½ .9383 * Stable
Neutron n 0 ½ .9396 * 882 p + e- + νe
Axion A0 0 0 ~ 10-4 Stable Hypothetical
X boson X +4/3 1 ~ 1015 * ~ 10-38 u + u or d + e+ Hypothetical
Y boson Y +⅓ 1 ~ 1015 * ~ 10-38 u + d or u + e+ Hypothetical
Magnetic monopole ? ? ~ 1017 Stable Hypothetical
Magnetic photon ? ? 0 Stable Hypothetical
Inflaton ? 0 ? ~ 10-34 ? Hypothetical
All of these particles are fundamental (not composed of smaller particles) except the proton and neutron.
If no half life is given in the table, the particle is stable (as far as we know).
As neutrinos propagate they can change to other kinds of neutrinos.
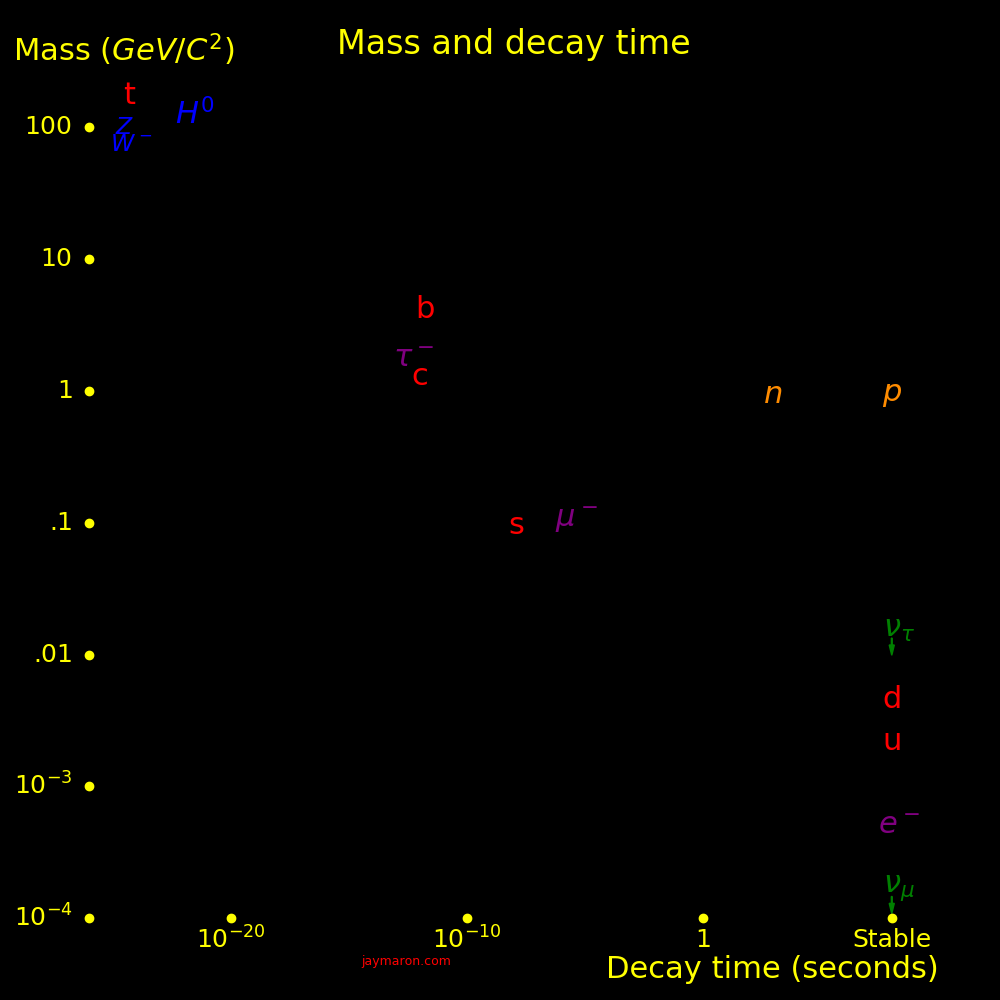 |
|---|
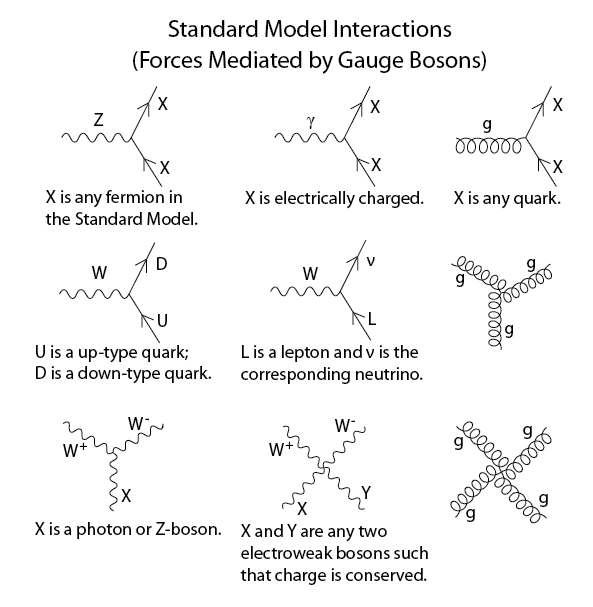 |
|---|
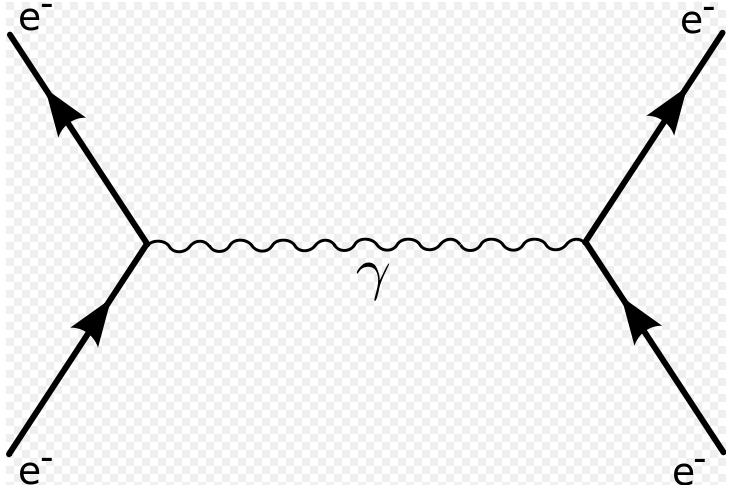
Feynman diagrams are a way of illustrating the possible particle interactions. In the above diagram, two electrons interact by exchanging a photon.
The W boson interacts with "weak isospin", and the Z boson interacts with "weak charge".
All interactions conserve weak isospin and weak charge, except for interactions with the Higgs boson.
Interactions with the Higgs boson break conservation of weak isospin and weak charge, but they conserve Q = 2 I - w.
Weak charge = w Weak isospin = I Electric charge = Q = 2 I - w
The weak force also has a "weak hypercharge", defined as W = Q - w.
Q W w I
Up quark 2/3 1/3 1/3 1/2
Down quark -1/3 1/3 -2/3 -1/2
Electron -1 -1 ~0 -1/2
Neutrino 0 -1 1 1/2
W+ 1 0 1 -1
Z 0 0 0 0
Higgs 0 1 -1 -1/2
Photon 0 0 0 0
Gluon 0 0 0 0
Graviton 0 0 0 0 Hypothetical
X 4/3 5/6 1/2 1/2 Hypothetical
Y 1/3 5/6 1/2 -1/2 Hypothetical
 |
|---|
1687 Earth gravity + Planetary motion → Newtonian gravity Newton
1750 Vitreous charge + Resinous charge → Electric charge Franklin
1752 Lightning + Electric charge Franklin
1820 Electric current + Magnet → Electromagnetism Oersted
1820 North magnetic fluid + South magnetic fluid → Magnetic field Ampere
1862 Electric force + Magnetic force → Maxwell's equations Maxwell
1864 Electromagnetism + Light → Elecromagnetic waves Maxwell
1905 Electromagnetism + Lorentz transform → Special relativity Poincare, Lorentz, Einstein
1915 Newtonian Gravity + Special relativity → General relativity Einstein
1926 Newtonian mechanics + Schroedinger eq. → Quantum mechanics Schroedinger
1928 Quantum mechanics + Special relativity → Dirac theory Dirac
1948 Quantum mechanics + Special relativity → Quantum electrodynamics Feynman, Schwinger, Tomonaga, Dyson
1954 Quantum electrodynamics + Gauge theory → Quantum field theory Yang, Mills
1967 Electromagnetism + Weak force → Electroweak force Salam, Glashow, Weinberg
1979 Strong force theory developed (Quantum Chromodynamics).
The theories of the strong and electroweak forces are not unified.
The theories of the strong and electroweak forces are collectively called the Standard Model
Future Electroweak force + Strong force → Grand Unified Theory (GUT)
Future Grand Unified Theory + General Relativity → Quantum Gravity
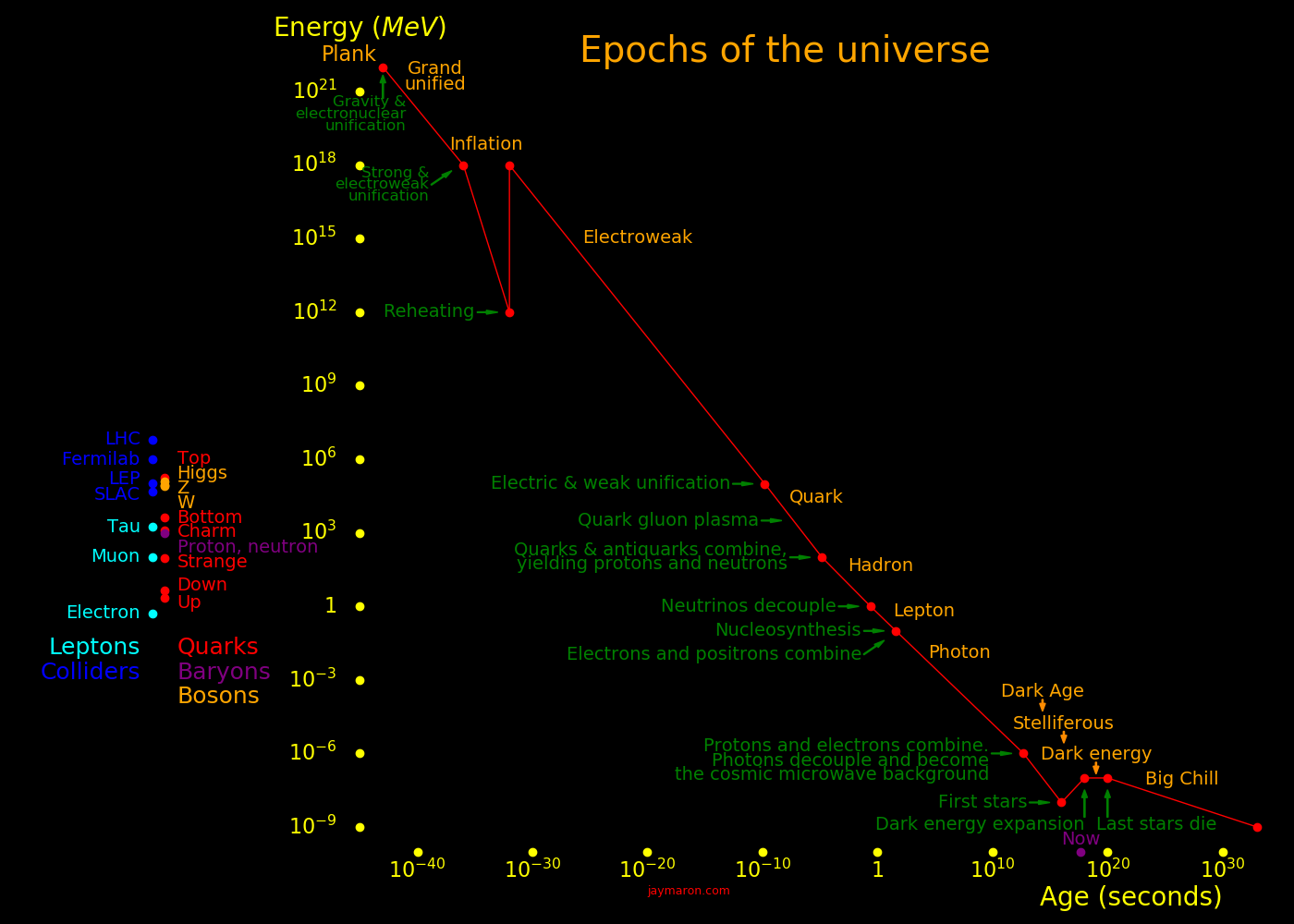
Epoch End time End energy Forces Particles
seconds MeV
Planck 10-43 1022 Quantum gravity Unknown
Grand Unified 10-36 1018 Electronuclear, gravity Unknown
Inflation 10-32 1018 Strong, electroweak, inflation Unknown
Electroweak 10-9 105 Strong, Electroweak Unknown
Quark 10-6 102 Strong, weak, electric, gravity Quarks, antiquarks, leptons, antileptons
Hadron 100 100 Strong, weak, electric, gravity Protons, neutrons, electrons, positrons. Neutrinos decouple from matter at this time
Lepton 101 10-1 Strong, weak, electric, gravity Protons, neutrons, electrons, positrons. Big Bang nuclearsynthesis occurs during this epoch
Photon 1013 10-6 Strong, weak, electric, gravity Protons, neutrons, electrons
Dark Age 1016 10-8 Strong, weak, electric, gravity Protons, neutrons, electrons
Reionization 1018 10-7 Strong, weak, electric, gravity Protons, neutrons, electrons
Dark energy 1020 10-7 Strong, weak, electric, gravity Protons, neutrons, electrons
Big Chill 10∞ <10-9 Strong, weak, electric, gravity Protons, neutrons, electrons
Planck: all the forces were unified.
Grand Unified: The strong and electroweak forces are unified as the electronuclear force. Gravity is a separate force and weaker than the electronuclear force.
Inflation: The universe expands by a factor of 1022 over a time of 10-32 seconds, undergoing supercooling during this time. After the conclusion of inflation, the energy of the inflation field goes to reheating the particles.
Electroweak: The strong force is separate from the electroweak force.
Quark: The electric force is separate from the weak force. Quarks are still too energetic to be bound to each other. The universe consists of almost equal numbers of quarks and antiquarks.
Hadron: The universe has cooled enough so that quarks can become bound into hadrons (baryons and mesons). Most of the quarks and antiquarks annihilate, leaving behind only quarks. Neutrinos are still energetic enough that they strongly interact with other particles.
Lepton: The hadron epoch ends when neutrinos are cold enough that they decouple from other particles. The universe consists of almost equal numbers of leptons and antileptons.
Photon: The universe has cooled enough so that most of the leptons and antileptons annihilate, leaving behind only leptons.
Dark age: The univese had cooled enough so that nuclei and electrons can combine. This is the end of the plasma age.
Stelliferous: Matter has collapsed gravitationally and formed stars.
Dark energy: The universe has expanded enough so that dark energy now dominates the expansion, and the expansion accelerates. All galaxies except those in the local group are accelerated beyond the cosmic horizon. We are in the beginning of this age.
Big Chill: After a trillion years the last stars burn out and the universe goes dark.
It is likely that protons decay on a timescale of 1036 years. If this happens, protons will decay to positrons and annihilate with electrons, leaving behind only photons.
After 1070 years, black holes evaporate by Hawking radiation.
 |
 |
|---|---|
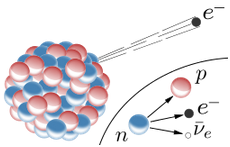
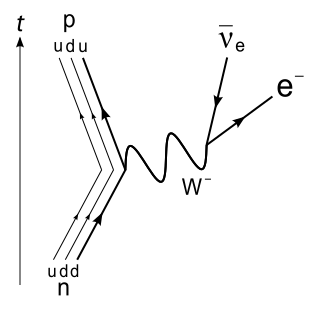
Beta decay changes a neutron into a proton, an electron, and an electron antineutrino. At the quark level it changes a down quark into an up quark.
p = u + u + d n = u + d + d d → u + W- → u + e- + νe n → p + e- + νe
The only bosons capable of changing particle identity are the W and Z, and this is how particles decay. For example, the τ particle decays as:
τ → W- + ντ
The W- then decays. Their ability to change particle identity is reflected in their decay modes, which are:
W+ → u + d W+ → u + s W+ → u + b W+ → c + d W+ → c + s W+ → c + b W+ → e+ + νe W+ → μ+ + νμ W+ → τ+ + ντ Z → e- + e+ Z → μ- + μ+ Z → τ- + τ+ Z → νe + νe Z → νμ + νμ Z → ντ + ντ Z → u + u Z → d + d Z → c + c Z → s + s Z → b + b
The W and Z bosons can't decay to a top quark because the top quark is heavier. The top quark decays as:
t → b + W+
Particle masses can be expressed in terms of electron Volts.
1 Electron Volt (eV) = The energy gained by an electron upon falling down a potential of 1 Volt.
= 1.602 Joules
M = Particle rest mass
C = Speed of light
E = particle rest energy
= M C2
Electron mass = 9.11 kilograms
= 511000 eV
1 keV = eV
1 MeV = eV
1 GeV = eV
Mass (GeV)
Electron .00051
Proton .9383
Neutron .9396
SLAC limit 45 Heaviest particle that can be produced by the Stanford Linear Accelerator
Higgs Boson 125 Discovered at the LHC
Fermilab limit 200 Heaviest particle that can be produced by Fermilab
LHC limit 700 Heaviest particle that can be produced by the Large Hadron Collider
Cosmic rays 1012 Highest-energy events observed
Big bang energy 1019 Energy of particles at the time of the big bang
Big bang energy = Planck energy
= 1.22 GeV
= 1.956 Joules
= 2.2 kg C2
The "Standard Model" describes:
The strong force (quantum chromodynamics)
The electroweak force
The Higgs particle and the mechanism for generating mass
Dark matter, dark energy, and matter-antimatter asymmetry are examples of
things that are not explained by the Standard Model.
String theory is an attempt to construct a theory of quantum gravity.
1803 Young discovers the diffraction of light, suggesting that light is a wave
1861 Maxwell develops the "Maxwell's equations", unifying electricity and magnetism
1864 Maxwell finds that light is an electromagnetic wave
1900 Planck solves the blackbody problem by assuming that photon energy is quantized as
E = h F
1905 Einstein publishes the "photoelectric effect" experiment, providing the first
direct measurement of photon energy and momentum.
1905 Theory of special relativity completed.
Einstein publishes the photoelectric experiment
1924 de Broglie postulates that for particles with mass,
Momentum * Wavelength = PlanckConstant
1927 Davisson and Germer experimentally verify the de Broglie relation for electrons.
Photons have zero rest mass. In 1924 de Broglie found that this equation
also applies to particles with finite rest mass. W is the "quantum-mechanical
wavelength" of a particle.
Photon frequency = F Photon wavelength = W Photon speed = C = 3.00⋅108 meter/second Planck constant = h = 6.62⋅10-34 Joule second Photon momentum = Q Photon energy = E Wave equation C = FW Energy equation E = hF Momentum equation E = QC de Brogie equation h = QW
Photons have zero rest mass. In 1924 de Broglie found that the equation h=QW also applies to particles with finite rest mass. W is the quantum-mechanical wavelength of a particle.
For particles with positive rest mass, we add the following variables.
Speed = V Lorentz gamma = γ = (1-V2/C2)-½ Rest mass = m Relativistic mass = M = γ m
The following equations apply for all particles, whether the rest mass is zero or positive.
Q W = h de Broglie equation E = (mC2)2 + (QC)2
If the particle has zero rest mass (m=0), such as a photon, the equation reduces to:
E = Q C
A photon has an effective relativistic mass of
E = M C2
If the particle has positive rest mass then
E = M C2 Q = M VIn many cases you can transform a classical formula to a relativistic formula by replacing "m" with "M", such as above.
If you try to accelerate a particle to the speed of light,
V/C → 1 M → ∞ Acceleration → 0The particle never reaches the speed of light.
 |
|---|
We can define 4 regimes.
Classical V/C << 1 Relativistic V/C not close to zero and not close to 1 Ultrarelativistic V/C close to 1 but not equal to 1 Photon V/C = 1
The classical regime is a simplification of the relativistic equations.
The ultrarelativistic regime can often be approximated with the photon regime.
If the simplified regimes are not sufficiently precise then you have to use the full relativistic equations.
V/C → 0 M → m γ → 1 + ½ V2/C2 E → E = m C2 + ½ m V2 A rest energy plus a kinetic energy Q → m V
For particles with zero rest mass, such as photons,
E = Q C
E → Q C
The following table shows example values for the properties of particles.
Rest Kinetic V/C Wavelength Compton radius
mass energy (angstroms) (amgstroms)
(MeV) (MeV)
Infrared photon 0 .0000001 1 107000 107000
Green photon 0 .0000023 1 5550 5550
X ray photon 0 .01 1 1.28 1.28
Gamma ray photon 0 5 1 .0026 .0026
Electron .511 0 0 - .0243
Electron from vacuum tube .511 .00001 .00626 12.3 .0243 10 electron Volts
Electron from beta decay .511 5 .9957 .0025 .0243
Electron at SLAC .511 45000 .999999999936 .00000028 .0243
Pion
Proton 938 0 0 - .0000132
Proton in nucleus 938 5 .103 .00013 .0000132
Proton at the LHC 938 7000000 .9999999910 .0000000018 .0000132
Cosmic ray proton 938 e15 nearly 1 1e-17 .0000132
Higgs boson 125000 0 0 - .0000000099
Baseball pitch e29 e15 .00000015 1e-24 e-24 146 grams, 45 m/s
F-22 Raptor, Mach 2.3 e36 3e22 .0000023 5e-31 e-41 20 tons, 700 m/s
Planck particle e22 e22 nearly 1 e-25 e-25
E = Energy
C = Speed of light
m = Rest mass
Q = Momentum
h = Planck constant
Particle energy and momentum are related by
E2 = (mC2)2 + (QC)2 If Q << mC the particle is nonrelativistic If Q = mC the particle is at the boundary between nonrelativistic and ultrarelativistic If Q >> mC the particle is ultrarlativisticIf the particle is on the boundary (Q=mC) then its wavelength is called the "Compton wavelength". For force-carrying particles this sets the range of the force.
Compton wavelength = h / Q = h / (mC)A F-22 Raptor has the same kinetic energy as a Planck particle.
A baseball pitch has the same Compton wavelength as a Planck particle.
The energy of a particle can be expressed as a rest energy plus a kinetic energy
E = Gamma m C2 = m C2 + (Gamma - 1) m C2 = m C2 + 1/2 m V2 in the limit of V/C << 1If Gamma < 2, a particle's rest energy is larger than its kinetic enegy.
In the Stanford Linear Collider (SLAC), electrons are accelerated to an energy of 45 GeV and collided head-on with antielectrons with the same energy.
Rest energy of electron = .0005 GeV Kinetic energy of SLAC electron = 45 GeVSLAC electrons are highly relativistic. When a SLAC electron is collided with a SLAC antielectron, they annihilate and new particles are created. The energy available to create new particles is 90 GeV. This is how a high-energy collison can produce particles that have a larger rest energy than the colliding particles.
For example,
Electron with 45 GeV + Antielectron with 45 GeV -> Annihilate
-> Charm Quark + Anti Charm Quark + 87.4 GeV of kinetic energy
Energy in GeV
Electron .0005
Proton 1.0
Neutron 1.0
Charm Quark 1.3
Higgs Boson 125
Big Bang particle 1019 GeV Energy required for quantum gravity
Quantum Relativistic Strong Planck Example
phenomena speeds gravity energy
Classical physics Rugby
Special relativity * Interstellar spaceships
General relativity * * Black holes
Quantum mechanics * Atomic sizes & smaller
Quantum field theory (QFT) * * Particle colliders
Quantum gravity * * * * Big bang
Quantum mechanics is relevant if the scale is equal to or less than the quantum
wavelength. If an object is larger than the quantum wavelength it behaves
classically.
In atoms, the size scale is small enough for quantum phenomena and the characteristic speeds of electrons are nonrelativistic, and so this is the regime of "Quantum mechanics".
Q = Momentum h = Planck Constant = 6.62e-34 Joule second W = Wavelength = h/Q meter K = Electric force constant = 8.988e9 Newton meter2 / Coulomb2 q = Proton charge = 1.602e-19 Coulombs G = Gravity constant = 6.67e-11 Newton meter2 / kg2 V = Velocity C = Speed of light R = Distance from the object Re = Object event horizon radius = 2 G M / C2 If V << C Special relativity may be neglected If V > 0.1 C Special relativity applies If W << R Quantum mechanics doesn't apply If W >= R Quantum mechanics applies If R >> Re Spacetime is flat enough for general relativity to be neglected If R < 10 Re Gravity warps spacetime and general relativity appliesIf gravity is strong enough to make particles relativistic and if the scale is small enough for quantum mechanics, quantum gravity is relevant. This is the "Planck scale". The space near an event horizon can make particles relativistic but a solar mass black hole is too large for quantum mechanics. Quantum gravity occurs at the centers of black holes and during the big bang.
As the mass of a particle increases, its event horizon radius increases and its quantum-mechanical wavelength decreases. When they become equal, quantum-gravity applies. THis is the "Planck scale".
For an ultrarelativistic particle,
E = Q C = h C / WIf the event horizon radius equals the quantum wavelength,
W = (G h / C3)½ = 4.1*10-35 meters This is the Planck scale
The physical constants can be used to define a universal set of units called "Planck units".
Planck distance = X Planck time = T Planck mass = M Photon energy = E = h f Photon frequency = f Speed of light = C = 2.998⋅108 Meters/Second Gravity constant = G = 6.674⋅10-11 Newton (Meter/Kg)2 Electron charge = e = 1.602⋅10-19 Coulombs Planck constant = h = 6.626⋅10-34 Joule Seconds Reduced Planck constant= ℏ = h (2π)-1 = 1.055⋅10-34 Joule SecondsWhen discussing Planck units, ℏ is used instead of h.
Speed of light: X = C T Gravitational energy: E = G M2 / X -> C2 = G M / X Energy quantization: E T = ℏ -> M C2 T = ℏSolving for {X, T, M},
Planck length = X = (G ℏ / C3)½ = 1.62⋅10-35 meters Planck time = T = (G ℏ / C5)½ = 5.39⋅10-44 seconds Planck mass = M = (ℏ C / G)½ = 2.18⋅10-8 kg = 1.22⋅1019 GeVThese are the scales for particles at the time of the big bang.
R = Distance between two particles M = Planck mass in kg = (ℏ C / G)½ m = Proton mass in kg = 1.673⋅10-27 kg Q = Planck charge in Coulombs q = Charge on the proton = 1.602e-19 Coulombs Fg = Gravity force = G M2 / R2 Fe = Electric force = K Q2 / R2 G = Gravity constant = 6.67e-11 Newton Meter2 / Kg2 K = Electric constant = 8.988e9 Newton Meter2 / Coulomb2The Planck charge is defined such that
Electric force between two Planck charges = Gravitational force between two Planck masses
G M2 = K Q2
Q = (ℏ C / K)½
= 1.876⋅10-18 Coulombs
q/Q = Proton Charge / Planck charge = .0854
m/M = Proton mass / Planck mass = 7.68⋅10-20
For two protons,
Gravity force / Electric force = G m m / (K q q) = (m/M)2 / (q/Q)2 = 8.087⋅10-37Gravity is vastly weaker than the electric force. This is because the proton mass is much less than the Planck mass, while the proton charge is similar to the Planck charge.
We can define a measure of the strength of the electric force "Z" by using photons. Suppose two electrons are a distance R apart and a photon has wavelength W = 2 π R. The photon energy is E = hf = hC/W.
R = Distance between two electrons f = Photon frequency W = Photon wavelength = 2 π R h = Planck constant E = Photon energy = h f = h C / W = ℏ C / R q = electron charge Ee = Electric energy between the electrons = K q2 / R α = Electric energy / Photon energy = (K q2 / R) / (hC/W) = 2 π K q2 / (hC) = .007297The dimensionless number α appears everywhere in physics and is called the "fine structure constant". For example,
Z = Proton charge / Planck charge = q K½ (ℏ C)-½ = .0854 = α½ R_classical / R_compton = α / (2Pi) R_classical / R_quantum = α2 / (2π)2
G = Gravitational force constant = 6.67*10-11 Newton Meter2 / Kilogram2 C = Speed of light M = Mass of a black hole m = Rest mass of a particle R = Distance between the black hole and the particle F = Force on a particle from the black hole E = Potential energy of the particle with respect to the black hole Re= Black hole event horizon radiusIf the particle is far from the black hole then the Newtonian formulas for force and energy apply
F = G M m / R2 E = -G M m / RAs the particle falls toward the black hole its velocity approaches C and the gravitational energy approaches the rest energy. General relativity becomes important here, and the characteristic scale R for this to happen is determined by C, G, and M. The only combination of these variables that gives units of length is
R = DimensionlessConstant * C2 / (GM)This is an estimate for the radius of a black hole event horizon. Order-of-magnitude estimates like this tend to give the right exponents (C2, G-1, M-1) but they can't give the dimensionless constant in front. Using general relativity, the exact formula for the event horizon radius is
Re = 2 C2 / (GM)The dimensionless constant turns out to be "2".
We can also estimate the event horizon radius by setting the gravitational energy equal to the rest energy.
G M m / R = .5 m C2 R = 2 G M / C2This is only an estimate because the Newtonian formulas break down near the black hole.
Plugging in the values for C and G,
Event horizon radius = 2 * 6.67e-11 / (3*108 m/s)2 * M
= 1.49e-27 * M
= 3000 meters * (M / Mass of sun)
If the sun were a black hole the event horizon radius would be 3000 meters.
To make the Earth a black hole you would have to squash it to a radius of
7 millimeters.
Neutron stars have a mass between 2 and 4 solar masses and a radius slightly larger than the event horizon radius.
The black hole at the center of the galaxy has a mass of 4 million solar masses and an event horizon radius of 12 million km. This is 1/12 the distance from the Earth to the sun.
In classical physics, an accelerating charge emits synchrotron photons and loses energy. If an electron orbits a proton then the emitted photons cause the electron to inspiral into the proton in 10-15 seconds. This is an example where a theory predicts a phenomenon that breaks the theory, and this usually points the way to a more fundamental theory. The thing that stops the electron from crashing into the proton is quantum mechanics.
Suppose an electron is on a circular orbit around a proton.
R = Distance between the electron and the proton V = Velocity of the electron C = Speed of light = 3.00e8 m/s M = Electron rest mass = 5.68e-31 kg Z = Electric charge on an electron = 1.602e-19 Coulombs K = Electric force constant = 8.988*109 Newton Meter2 / Coulomb2 F = Force between the proton and electron = -K Z2 / R2 E = Electron kinetic energy = .5 M V2 Ee = Electric energy between the proton and electron = Integral (Force dR) = -K Z2 / R Q = Electron momentum = M V h = Planck Constant = 6.62 * 10-34 Joule seconds W = Electron quantum-mechanical wavelength = h / QBalance the electric and the centripetal forces:
K Z2 / R2 = M V2 / RThe kinetic energy is
E = .5 M V2 = .5 K Z2 / RThe electron becomes relativistic when E ~ M C^2. Define
R_classical = Classical radius of the electron
= Radius of a circular orbit for which the kinetic energy equals the rest energy
= K Z2 / (M C2)
= 2.818e-15 meters
If R < R_classical, classical physics is guaranteed to fail and so some new
physics has to appear. A similar example is a black
hole where Newtonian gravity breaks down and general relativity takes over.
The Schwarzschild radius of a black hole is the characteristic distance where infalling matter becomes relativistic.
M = Mass of an electron
M_hole = Mass of a black hole
E_grav = - G M_hole M / R2
R = Distance of an electron from a black hole
R_schwarz= Schwarzschild radius of a black hole, the closest distance from which
light can escape.
= 2 G M / C2
Setting the gravitational energy equal to the rest energy gives the gravitational
radius of a black hole, which is proportional to the Schwarzschild radius.
As R->0, the scale where quantum mechanics becomes important is the "quantum radius of the electron".
To derive this scale we calculate the electron wavelength as a function of R. We assume that the electron is nonrelativistic and we assume the electron is on a circular orbit around the proton. The balance of electric and centripetal force is
W = Quantum-mechanical wavelength of the electrom R = Orbital radius of the electronThe parameter that characterizes the importance of quantum mechanics is W/R.
If W/R > 1 Quantum mechanics is important
If W/R < 1 Quantum mechanics is unimportant and classical physics can be used
W/R = (h/Q) * Q2 / (K q2 m)
= h Q / (K q2 m)
= Constant * R-½
As R-> Infinity W/R -> 0 Classical physics applies
As R-> 0 W/R -> Infinity Quantum mechanics applies
The radius where W/R=1 is the quantum radius of the electron.
R_quantum = h2 / (K q2 m)
= 2.086e-9 meters
We can compare the quantum radius to the classical radius.
R_quantum / R_classical = h2 C2 / (K2 q4)
= 740000
Because R_quantum / R_classical >> 1, quantum mechanics becomes important
before relativity.
R_quantum sets the size of atoms. If you calculate the electron orbital radius
in a hydrogen atom using the Bohr theory,
R_bohr = R_quantum / (2 Pi)
= 5.29e-11 meters
This is the radius of the S=1 orbital in a hydrogen atom.
If a particle is nonrelativistic (V << C),
Q = Momentum = m V E = Energy = ½ m V2 Q2 = 2 m EIf a particle is relativistic (V~C),
E ~ Q CFor relativistic particles we can define an equivalence between space and time by setting V=C.
Space = C * TimeWe can also define an equivalence between space and energy by setting the space scale equal to the quantum mechanical wavelength.
E = Q C = h C / WIf we set E equal to the particle's rest energy, we call the resulting wavelength the "Compton wavelength". This particle is "barely relativistic".
m C2 = h C / R_compton R_compton = h / (m C)All particles with finite mass have a Compton wavelength.
Suppose a photon has an energy equal to a particle's rest energy E.
f = Photon frequency W = Photon wavelength E = h f = h C / W W = h C / E = h / (M C)The wavelength of the photon is equal to the particle's Compton wavelength. If a photon has the same energy as a particle's rest energy the wavelength of the photon is equal to the Compton wavelength.
For an electron,
R_compton = 2.426e-12 meters
m = Particle rest mass E = Particle rest energy = m C2 T = Particle lifetime X = Characteristic distance a virtual particle travels during its lifetime h = Planck constant Q = Particle momentum C = Speed of lightFrom the Heisenberg uncertainty principle, a virtual particle has a characteristic lifetime such that
E T = hVirtual particles are relativistic and so we assume V ~ C.
The distance the virtual particle travels in its lifetime is
X = T C = h C / EIf we set E equal to the rest energy mC2,
X = h / (m C)This is the "Compton wavelength" of a particle.
Force Force carrying Mass of force Compton radius of
particle carrying particle force-carrying particle
(GeV) (meters)
Gravity Graviton 0 Infinite
Weak W 80 1.5e-17
Z 91 1.4e-17
Electromagnetic Photon 0 Infinite
Strong Pion .135 9.2e-15
Technically the strong force is carried by gluons.
For protons and neutrons in a nucleus the strong force can be considered to be
carried by pions.
If a force is carried by a massless particle then the force is given by
Force = Constant / R2such a force is said to have "infinite range".
If the force is carried by a massive particle then the force is said to have "finite range". The range of the force is equal to the carrier's Compton wavelength and beyond this range the force is essentially zero.
The size scale of the nucleus is determined by the pion's Compton wavelength.
The force-carrying particles for the weak force are heavy and hence the weak force has short range, 100 times shorter than the size of a nucleus. This is why the weak force is weak.
The fine structure constant characterizes the strength of the electromagnetic force.
For two electrons, the gravitational force is vastly weaker than the electric force.
Force of gravity / Electric force = G m2 / K q2 = 2.40e-43
Quantum mechanics resolved the electron crisis. The next crisis is the Higgs crisis.
Higgs mass = 125.3 GeV
meters
Electron quantum radius 2.09e-9 Limit for classical physics
Atomic scale 2e-10
Electron Compton radius 2.43e-12 Limit for non-relativistic quantum mechanics
Electron classical radius 2.82e-15
Nuclear scale 1e-15
Higgs Compton radius 9.9e-18
Suppose we consider a length scale R.
If R > Electric quantum radius Classical physics applies If R < Electron quantum radius Quantum mechanics apples If R > Electron Compton radius Non-relativistic quantum mechanics may be used If R < Electron Compton radius Relativistic quantum mechanics must be used If R > Higgs Compton radius The Standard Model applies If R < Higgs Compton radius The Standard Model breaks downThe Standard Model breaks down for scales below the Higgs scale and some new theory must take over for smaller scales. The most promising candidates are "Supersymmetry" and "The Multiverse". The Large Hadron Collider can at present explore down to the Higgs scale but no further. When it is upgraded to higher energies in 2015 it will be able to go beyond the Higgs scale.
There is much drama in the world of supersymmetry. It is predicted that the LHC should already have detected supersymmetric particles and thus far none have been found.
kg/m3
Planck density 5 ⋅1096 = PlanckMass / PlanckLength^3
Solar system 2 ⋅10-8 = Mass of sun / (30 AU)^3
Milky Way 3 ⋅10-21 = 1.2e12 solar masses / (100000 lightyears)^3
Matter .12⋅10-27 Mean density of protons & electrons in the universe
Dark matter .66⋅10-27 Mean density of dark matter in the universe
Dark energy 1.67⋅10-27 Mean density of dark energy in the universe
As the universe expands the matter and dark matter density decrease and the
dark energy density is constant.
In the early universe the dark matter density was vastly greater than the dark energy density. In the future dark energy will overwhelm dark matter and the universe will expand unchecked.
Tangible matter = Stuff that interacts by the strong and/or electromagnetic force,
such as protons, neutrons, electrons, photons.
These particles can be stopped by a meter of lead.
Dark matter = Stuff that does not interact by the strong or electromagnetic
force but interacts by the weak force and gravity.
These particles easily pass through the Earth.
Examples include neutrinos.
Most of the dark matter in the universe consists of particles
that have not yet been discovered.
Dark energy = An energy density that has negative pressure.
Tangible matter and dark matter have positive pressure and dark energy has negative
pressure. All three have positive energy density.
Densities:
kg/m3
Planck density 5 *1096 = PlanckMass / PlanckLength^3
Black hole 1.8 *1019 = Density of a 1 solar mass black hole
Neutron star 1 *1018 = Upper range for the density at the core
Nuclear matter 2.3 *1017 = Density of a nucleus
White dwarf 1 *109 = White dwarf density
Osmium 22.6 *103 = Densest element
Water 1 *103
Air 1.22*100 At sea level
Solar system 2 *10-8 = Mass of sun / (30 AU)^3
Milky Way 3 *10-21 = 1.2e12 solar masses / (100000 lightyears)^3
Ordinary matter .12*10-27 = Mean density of protons, neutrons, & electrons in the universe
Dark matter .66*10-27 = Mean density of dark matter in the universe
Dark energy 1.67*10-27 = Mean density of dark energy in the universe
Sum 2.45*10-27 = Total density of matter, dark matter, and dark energy
As the universe expands the matter and dark matter density decrease and the
dark energy density is constant.
In the early universe the dark matter density was vastly greater than the dark energy density. In the future dark energy will overwhelm dark matter and the universe will expand unchecked.
The Earth's escape velocity is Ve=11.2 km/s. Suppose the Earth had no atmosphere and you launched a cannonball upward with velocity V.
V < Ve Elliptic The cannonball falls back to the Earth
V > Ve Hyperbolic The cannonball escapes from the Earth and asymptotes to a
positive velocity
V = Ve Parabolic The cannonball is on the boundary between escape and falling back.
It never returns to the Earth and it asymptotes to zero velocity.
If the universe consisted entirely of ordinary matter and dark matter and no
dark energy, then there is a critical value of the density such that the
expansion of the universe is parabolic. This value is 2.45e-27 kg/m3.
d = Density of a parabolic universe = 2.45e-27 kg/m3 D = 1.0 = Density of all matter and dark energy in the universe / d Dom = .049 = Fraction of ordinary matter in the universe / d Ddm = .27 = Fraction of dark matter in the universe / d Dde = .68 = Fraction of dark energy in the universe / dD, Dom, Ddm, and Dde are scaled relative to the parabolic density d.
If Dde = 0 then
If D > 1 The density of the universe is large enough to reverse the expansion from
the big bang and the universe collapses in a Big Crunch.
The Hubble constant goes from positive to zero to negative.
If D > 1 The universe expands forever, ending with a positive Hubble constant
If D = 1 The universe stops expanding and the Hubble constant goes to zero.
The universe ends in a "Big Chill".
If Dde > 0 then dark energy trumps all of the above. If the universe survives long
enough to avoid a Big Crunch then dark energy causes the universe to expand unchecked
regardless of the matter density. The universe ends in a Big Chill.
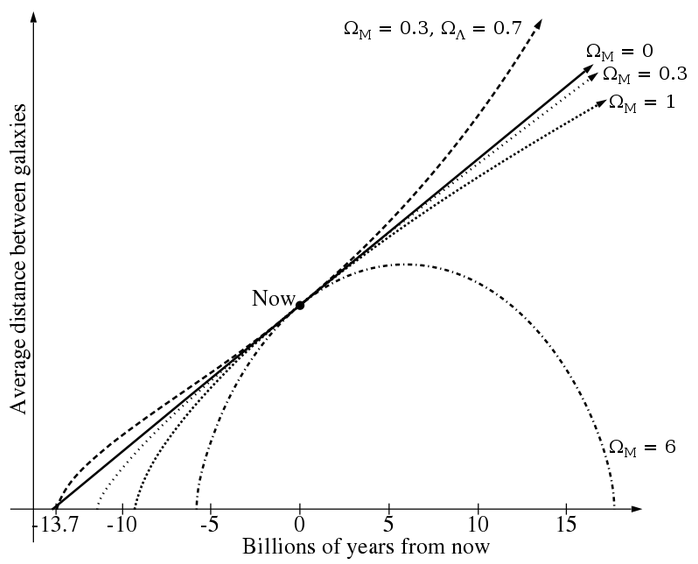
Previous to 2005 we knew that the value of D was close to 1 and we couldn't tell if it was larger or smaller than 1. The value of the dark energy density was unknown and the fate of the universe was unknown. The theory of "Inflation" was developed to explain why D is close to 1.
In 2005 measurements of distant supernovae showed that Dde > 0, implying that the universe will end in a Big Chill.
In 2010 the Planck spacecraft measured the precise values of Dom, Ddm, and Dde.
In the plot, Omega_M = Dom + Ddm Omega_Lambda = Dde
 |
|---|
You can illustrate the concept of escape velocity with the "My Solar System" simulation at phet.colorado.edu.
Mass Position Velocity
X Y X Y
Body 1 100. 0 0 0 0 Sun
Body 2 1. 100 0 Vx Vy Planet
If Vx=100 and Vy=0 the planet orbits the sun on a circular orbit.
What do the orbits look like if you vary Vx?
The escape velocity from the sun at X=100 is Ve=100*Squareroot(2).
If Vx=0 and Vy > Ve the planet escapes. If Vx=0 and Vy < Ve the planet crashes into the sun.
Scale Constituents of matter (meters) 1 Materials, gases, chemicals, pizza 10-9 Molecules 10-10 Elements (hydrogen, helium, ...) 10-14 Nuclei & electrons 10-15 Protons, neutrons, pions, electrons, photons, neutrinos, dark matter 10-16 Quarks, electrons, photons, gluons, neutrinos, W, Z, Higgs, dark matter
Number of Parameter
parameters
6 Quark masses. Up, down, charm, strange, top, bottom
3 Lepton masses. Electron, muon, tau
3 Neutrino masses. Electron neutrino, muon neutrino, tau neutrino
1 Z mass. The W mass is determined by the Z mass.
1 Higgs mass
1 Electric force constant
1 Gravitational force constant
1 Strong force constant
1 Weak force constant
4 3 Neutrino mixing angles and one phase
6 Cosmological parameters. These are:
Density of tangible matter in the universe (nuclei, electrons, etc)
Density of dark matter in the universe
Dark energy density (cosmological constant)
Scalar spectral index of the universe
Curvature fluctuation amplitude of the universe
reionization optical depth of the universe
Dark matter is likely a source of new parameters, such as the masses of the dark
matter particles.
The masses of the proton and neutron can be calculated from the masses of the up and down quark.
At present the origin of these parameters is unknown. Ideally, a future physics theory will explain the origin of the parameters based on a compact set of principles, and the number of parameters will decrease. This was the hope of Einstein. Since special relativity and general relativity can be generated from compact principles it was hoped that particle physics could as well, but at present no successful principles have been found.
An alternative to principles is The Multiverse, where there are multiple universes, each with different parameters, and we live in a universe where the parameters allow for the existence of intelligent life. This is similar to the Anthropic Principle.
If you change the parameters of the universe there are extreme consequences. For example,
If the electron mass increases, protons will consume the electrons to produce neutrons, leaving behind a boring universe with no nuclei.
If the dark energy density is increased, the universe expands too fast for galaxies to form.
If you increase the electric force relative to the strong force then nuclei can't form.
Possibilities for the laws of physics:
Natural The parameters of the universe will be found to originate
from compact principles and no fine tuning is required for life.
Fine tuned The parameters of physics require fine tuning to be
amenable to life.
Intelligent design The parameters of the universe were designed to be amenable
to life.
Multiverse There are multiple universes with different laws of physics,
most of them dull and lifeless, but the probability of one of
them accommodating life is unity.
Fortuitous There is only one universe. The laws of physics require fine
tuning and we are lucky that they are amenable to life.
Matrix The universe is a computer simulation.
Darwin universe Universes beget universes and the laws of physics evolve
by natural selection.
An analogue of The Multiverse is the Drake equation.
P = Probability that a star has a planet with intelligent life
N = Number of stars in the universe.
If:
P ~ 1 Life is natural
P << 1 Life requires fine tuning
P << 1 and PN >> 1 Life requires fine tuning but life is probable in the universe.
This is the "Anthropic principle" or the "Multiverse" scenario.
P << 1 and PN << 1 Life is improbable in the universe.
Either life is "Lucky" or we live in The Matrix or the
Earth was intelligently designed.
 |
|
|---|---|
The rules of soccer are "natural" in the sense that they flow from a single premise (don't use your arms) and they lead to a rich game. The rules of football are "unnatural" in that the rulebook is thick and it takes a squad of referees to enforce.
 |
|---|
The notes for 12-tone equal temperament coincide well with the note of just intonaton.
The most resonant notes in the 12-tone equal temperament scale are the fourth and the fifth and these are particularly close to their just-intonation counterparts.
The frequency ratio between a fourth and a fifth in just-temperament is
R = (3/2) / (4/3) = 9/8 = 1.125In a 12-tone equal-tempered scale the frequency ratio of a whole step is
R = 2(2/12) = 1.122which is nearly the same as the ratio between a fourth and a fifth. This is why the 12-tone scale works so well. If you try any number other than 12 it doesn't work. This is why the 12-tone scale is the most useful for writing harmony.
Tunings exist that use numbers different from 12, such as for Indian, Thai, and Arabic music. These tunings can generate exotic melodic structure but they are less useful for harmony than the 12-tone scale.
The 12-tone scale is natural in the sense that it doesn't have any "free parameters". The choice of the number "12" emerged naturally from the positions of the resonant notes. It is also "fortuitous" in that the values of Z are so small.
Soccer is an example of a "natural sport". The rules are simple and if you change the parameters (such as field size, number of players, etc) the game is essentially the same.
American football requires "fine tuning". In order for the sport to make sense you need a large rulebook. It also has lots of "free parameters" because there are many different ways the rules could be constructed.
The chess player Edward Lasker once said:
"While the Baroque rules of Chess could only have been created by humans, the rules of Go are so elegant, organic, and rigorously logical that if intelligent life forms exist elsewhere in the universe, they almost certainly play Go."
The rules of chess are an example of "fine tuning" and there are lots of
free parameters (the moves allowed by each piece).
 |
|---|
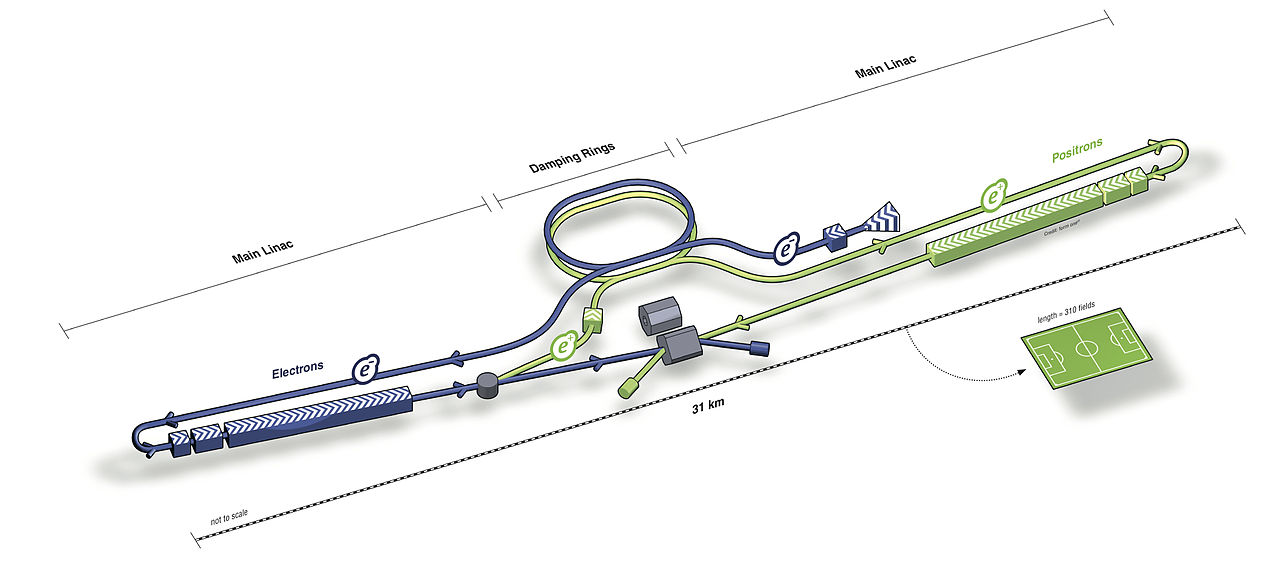
Particle physics is starved for data. The Large Hadron Collider discovered all particles it's capable of discovering and now we need a bigger collider. The options are a linear electron collider and a ring proton collider.
 |
 |
|---|---|
In a proton ring collider, a set of protons circles clockwise and another set circles counterclockwise, and they're arranged to collide.
In a linear electron collider, electrons start at one end and positrons start at the other end, and both are accelerated toward the center and arranged to collide.
Linear and ring colliders have contrasting strengths and weaknesses.
A ring proton collider can reach a higher energy than a linear electron collider.
Electron-positron collisions give more precise data than proton-proton collisions.
An electron ring collider has a maximum energy of .25 TeV, above which electrons lose energy to synchrotron radiation. This is why a high-energy electron collider has to be linear. Proton ring colliders don't have the synchrotron problem and can be arbitrarily large.
A linear electron collider that is longer than 100 km has to follow the Earth's curvature, giving it a maximum energy of 23 TeV. Above this energy, electrons lose energy to synchrotron radiaton.
In an electron-positron collision, if the electron energy is X, then the maximum energy of a particle that the collision can create is X. For proton-proton collisions, the maximum energy of a created particle is less, on the order of .15 X.
A linear collider can be built incrementally. You can always increase the length. A ring collider can't be made larger. However, you can use an existing ring collider as an injector for a bigger collider. A hypothetical strategy is to build a .25 TeV electron linear collider to study the top quark and Higgs boson, and then extend it beyond 1 TeV.
An electron linear collider is under consideration by CERN, to reside in Switzerland and France.
A proton ring collider is under consideration by China. The tunnel that hosts the proton collider will also host an electron ring collider at .2 TeV, for mass production of top quarks and Higgs bosons, to refine their measurements.
Type Particle Energy Size Year Particles discovered
GeV km
Stanford Linear Collider Linear Electron 45 3.2 1966 Up, Down, Strange, Charm, Tau
Super Proton Synchrotron Ring Proton 450 1.1 1976 W-, Z
Petra Ring Electron 20 .32 1978 Gluon
LEP Collider Ring Electron 104 4.3 1989
Fermilab Ring Proton 1000 6 1989 Bottom, Top
Large Hadron Collider Ring Proton 6500 4.3 2011 Higgs
Compact Linear Collider Linear Electron 3000 30 Future
China proton collider Ring Proton 75000 16 Future
Earth electron collider Linear Electron 30000 300 Far future
Earth proton collider Ring Proton 6000000 1000 Far future
"Collider size" is the radius for ring colliders and half the total length for a linear collider.
"Earth electron collider" is the largest electron linear collider that can be built on the Earth. Its maximum size is set by synchrotron radiation from the Earth's curvature.
"Earth proton collider" is the largest electron linear collider that can be built on the Earth. You need a large continental plate.
The LEP collider was dismantled and its tunnel now hosts the Large Hadron Collider.
 |
|---|
Particle diameter is proportional to Mass1/3.
The electron is exaggerated otherwise it would be invisible.
Blue particles represent the heaviest particle that can be produced by the accelerator.
At this scale, a Planck-mass particle has a diameter of 10 km.
Photons, Gluons, and Gravitons are massless.
The LHC is far from the Planck energy.
 |
|---|
 |
|---|
 |
 |
|---|---|
The energy of a linear accelerator is determined by length and force. The maximum force is .023 TeV/km using klystrons and .1 TeV/km using the dual-beam technique. To discover new physics, the energy has to be larger than 1 TeV. A 1 TeV accelerator based on the dual-beam technique has a length of 10 km.
Accelerator length = X = 10 km Force = F = .1 TeV/km Electron energy = E = X F = 1 TeV
 |
 |
|
|---|---|---|
In a ring collider, magnets steer protons around the ring. Ring colliders can add energy to particles each pass around the ring, and so they aren't limited by force. It's like spinning up a merry-go-round. Ring colliders are limited instead by the strength of the bending magnets. For the Large Hadron Collider,
Magnetic field strength = B = 5.4 Tesla (average field) Radius of the ring = R = 4300 meters Maximum particle energy = E = .00030 B R = 7.0 TeV
If an electron linear collider is long enough, it has to curve with the Earth's surface, and this limits the energy to 23 TeV. You can get to 30 TeV by having a straight section just before the collision.
You can make a long straight tunnel using mountains and by digging deep. The tunnel starts deep and ends at a mountain.
The deepest mines have a depth of 4 km and mountain ranges have a height of order 6 km, and this allows one to build a straight tunnel 100 km long.
The average thermal gradient of the Earth is 25 Celsius per km of depth. The deepest mines are:
Depth Rock temperature
km Celsius
Mponeng Gold Mine 4.0 66 South Africa
TauTona Gold Mine 3.9 60 South Africa
Savuka Gold Mine 3.7 South Africa
Driefontein Mine 3.4 South Africa
 |
 |
 |
|---|---|---|
An accelerating charged particle emits photons (synchrotron radiation). Particles traveling around a ring emit photons and lose energy. The larger the collider, the larger the particle energy and the larger the synchrotron loss rate. A ring collider can only be made so large before synchrotron loss exceeds energy gain from acceleration.
The synchrotron radiation power is
Particle energy = E Particle rest energy = Erest Ring radius = R Synchrotron radiation power = P ~ (E/Erest)4 / R2 Erest (Proton) ------------------- = 1836 Erest (Electron)Electrons have a smaller rest energy than protons and emit vastly more synchrotron radiation. An electron ring collider is limited by synchrotron radiation rather than by magnet strength. The maximum energy is .15 TeV. Generating electron energies larger than this requires a linear collider.
Protons emit negligible synchrotron radiation and the radiation is never a concern. Proton ring colliders are limited by magnet strength rather than by synchtrotron radiation.
Future colliders will consist of proton ring colliders and linear electron colliders.
Particle energy = E (TeV) Particle velocity = V Speed of light = C Particle charge = 1.602e-19 Coulombs Magnetic field = B (Teslas) Magnet strength averaged around the ring Collider radius = R Particle rest mass = m Particle relativistic mass = M Electric force constant = K = 8.988⋅109 Newton meter2 / Coulomb2 Electric force on a charge = Fe = q E Magnetic force on a charge = Fm = q V B Centripetal force = Fc = M V2 / RParticles in a collider are "ultrarelativistic" and so we may assume:
M >> m V ~ C E ~ M C2Particles are steered around the ring by magnets
Magnetic force = Centripetal force q B V = M V2 / R q B = E / (C R) E = q C B R E = .00030 B R (Energy in TeV)The maximum energy of a ring collider is determied by the magnetic field and the ring radius.
Magnets are a finicky technology and thus far the LHC magnets are not at full strength. The current proton energy is 4 TeV and an energy of 6.5 TeV is expected in 2015.
The Lorentz factor of a 7 TeV proton is γ = E/(mC) = 7460 = 7 TeV / .000938 TeV
If a charged particle is accelelerated it emits photons (synchrotron radiation). Particles in a ring collider emit synchrotron radiation when they are bent by the magnetic field.
Particle energy = E
Particle rest energy = Eo
Particle charge = q
Particle velocity = V
Speed of light = C
Electric force constant = K = 8.988⋅109 Newton meter2 / Coulomb2
Collider radius = R
Synchrotron power = P = (2C/3) K q2 (V/C)4 (E/Eo)4 R-2
Decelerating synchrotron force= Fs = P/V (Joules/meter)
Synch. energy loss / cycle = Es = (2πR/V) P Energy lost to synch. each ring trip
= (4πC/3V) K q2 (V/C)4 (E/Eo)4 R-1
~ (4π/3) K q2 (E/Eo)4 / R (Using V ~ C)
Fraction energy lost per cycle= Q = Es / E
Collider maximum energy = Emax
In order for a ring to be effective it must have Q << 1. If Q >= 1 then you might
as well build a linear collider. For a given collider radius R the synchrotron
energy limit is
Emax = Es / Q = (4/3 πKq2/Q) (Emax/Eo)4 R-1 Q-1
= (4/3 πKq2/Q)-1/3 Eo4/3 R1/3
The CERN ring has R = 4243 meters. If we set Q=1 we get the following energies:
Eo Emax
(TeV) (TeV)
Electron .000511 .27
Muon .106 325
Proton .938 5961
When the CERN ring housed the Large Electron Positron collider (LEP) it operated
at an energy of .104 TeV. The ring was subsequently converted to a proton collider
with an energy of 7 TeV. Proton synchrotron radiation is negligible at this energy.
The energy limit from synchrotron radiation has the form: E ~ R1/3 The energy limit from the bending magnets has the form: E ~ B RWhen these are equal, the energy and radius are "Er" and "Rr".
If R < Rr then E is limited by the strength of the magnets If R > Rr then E is limited by synchrotron radiationIf we set B = 10 Tesla and Q = 1 we get
Er (TeV) Rr
Electron .061 20 meters
Muon 2630 880 km
Proton 207000 69000 km = 11 Earth radii
An electron collider larger than 20 meters is limited by synchrotron radiation.
Any proton or muon collider that could conceivably be built on the Earth is limited by the bending magnets rather than by synchrotron radiation.
In a collider, a particle "X" collides with its antiparticle "x" and they annihilate to create a new particle-antiparticle pair Y and y.
X + x --> Y + yThe maximum rest mass of the Y particle is equal to the energy of the X particle. Hence, a collider that collides 1 TeV electrons with 1 TeV antielectrons can produce particles with a rest mass of up to 1 TeV.
Protons consist of three quarks. In a proton collision, new particles are produced by collisions between individual quarks. Since each quark carries only a fraction of the proton's total energy, not all of the proton's energy can be used to make new particles. At Fermilab, protons have an energ of 1 TeV and the heaviest particles it can create are the .171 TeV top quark and the .125 TeV Higgs boson. This gives electron and muon colliders an energy edge over proton colliders.
Electron and muon colliders can also tune the beam energy to be exactly equal to the rest energy of the particle they're trying to create, whereas the energy of a quark-quark collision can't be tuned. This means that electron and muon colliders can produce particles with greater rates than a proton collider.
Electron and muon collisions also produce less background particles than proton collisions, making the events easier to analyze.
If a collider follows the curvature of the Earth then the synchrotron energy limit is:
Collider radius = R = 6.371⋅106 meters (For the Earth) Particle energy = E = 23 TeV (For electrons limited by the Earth's curvature) Particle rest energy = Eo = .00000051 TeV (Electrons) Forward accelerating force = Fc = .0001 TeV/m (For the Compact Linear Accelerator) Synchrotron decelerating force = Fs = (2/3) K q2 (E/Eo)4 / R2If the collider force is equal to the synchrotron force,
E = Eo Fc1/4 R1/2 [(2/3) K q2]-1/4The following table gives the synchrotron energy limit for electrons, protons, and muons.
Radius Electron Muon Proton
TeV TeV TeV
Earth surface 6371 km 23 4800 43000
Orbit around Earth 10000 km 29 6000 53000
Earth orbit around sun 1.2 AU 6000 850000 7500000
Kuiper Belt orbit around sun 40 AU 53000 4700000 41000000
Light year radius 63200 AU 2109000 187060000 1630000000
Muons have a halflife of 2.2 microseconds. Muons in a collider live longer because of time dilation, and so they can traverse the ring many times before decaying.
Muon halflife = T = 2.2e-6 seconds
Collider radius = R
Magnetic field = B
Muon energy in TeV = E = .00030 B R (from the "ring colliders" section)
Muon Lorentz factor = Z = E / .000106 = E / Restenergy
Speed of light = C
Ring cycles = N = Z T C / (2 π R) (Trips around the ring in one halflife)
= (.00030 B R / .000106) T C / (2 π R)
= 297 B
A future muon collider would have B ~ 10 Tesla, and so the muons will traverse the
ring ~ 3000 times before decaying.
The obstacle to building a muon collider is the need for a muon cooling technology, currently under development at Fermilab. If this can be done, then muons could be used at the Large Hadron Collider.
Muons emit high-energy neutrinos, which is a hazard to nearby humans. A set of sample radiation parameters can be found in http://arxiv.org/pdf/hep-ex/0005006v1.pdf
Muon energy Radiation
(TeV) (mSieverts/yr)
2 .0005
5 2.3
50 10
Earth average background radiation is 3.5 mSieverts/yr. A muon collider with
energy > 5 TeV would have to be located at a remote site away from
civilization.
These are hypothetical colliders that could be built in the near or distant future. We assume a gradient of .1 TeV/km for linear colliders and a magnetic field of 10 Tesla for ring colliders.
Particle Shape Length or Energy
Radius (km) (TeV)
Electron Ring 13 .125 Higgs energy, to mass-produce the Higgs
Electron Linear 30 3 Compact Linear Collider
Proton Ring 4.2 7 Existing LHC
Electron Linear 800 80 Limited by synchrotron radiation from the Earth's curvature
Muon Linear 4000 400
Proton Ring 1000 600 Continent-sized
Electron Linear 1 AU 4200 Orbiting the sun between Earth and Mars. synchrotron limit
Muon Ring 10000 6000 Orbiting the Earth
Muon Ring 1 AU 106 Orbiting the sun between Earth and Mars. synchrotron limit
Muon Ring 100 AU 107 Orbiting the sun at the Kuiper belt, synchrotron limit
Muon Linear 1 LY 1012
An advanced civilization will likely find a way to improve the energy gradient, and hence a light year sized collider will likely reach the strong scale energy of 1013 TeV. Reaching the Planck energy of 1016 requires a substantial improvement in the energy gradient, or a colossally long collider.
The Planck energy is 1016 TeV. If the energy gradient is .1 TeV/km then the collider length is 1017 km = 10000 light years. This is 1/3 of the distance between the sun and the center of the Milky Way. Such a collider would have to be built in intergalactic space to escape the gravity of galaxies.
Collider Particle Type Energy Size Lum Power BeamX BeamY BeamZ Particles/ Particles/
TeV km MW nm nm nm second (1024) bunch
Stanford Linear Accel. e- Linear .045 3.2 .0003 64 2000 2000 .12
Large Electron Positron e- Ring .104 4.3 .01 18 200000 2000 3600.
Fermilab Proton Ring 1.0 1.0 .04 30000 30000
Large Hadron Collider Proton Ring 7 4.3 1 17000 17000 44000 29000.
Int. Linear Collider e- Linear .5 16 2 230 5.7
Compact Linear Collider e- Linear 3 30 6 240 40 1 .024
Higgs factory e- Ring .125 8.5 1.8 50
"Size" corresponds to radius for a ring collider and length for a linear collider.
"Lum" is the luminosity in 10^34 particles / cm2 / s
BeamX is the horizontal beam size
BeamY is the vertical beam size
Linear colliders tend to have a smaller beam cross section than ring colliders.
The "Circular Electron Positron" collider is a future collider that is optimized for generating Higgs particles.
Suppose we compare the tunnel lengths of a linear and a ring collider.
In an electron-positron collision, all of the particle energy can be harnessed for creating new particles. In a proton-proton collision, only a fraction of the energy is available for creating new particles.
Linear collider radius = Rl = 500 km
Linear collider energy gradient = G = .1 TeV/km
Linear collider energy = El = Rl G = 50 TeV
Ring collider radius = Rr = 83 km
Ring collider mean magnetic field = B = 10 Tesla
Ring collider constant = C = .30 TeV/Tesla/km
Ring collider reach factor = f = .2
Ring collider energy = Er = C B Rr = 250 TeV
= El/f
Radius ratio = Q = Rr/Rl = G (f C B)-1 = .17 for protons
= .033 for muons
What is the interplanetary magnetic field as a function of distance from the sun? What would you estimate is the lowest-energy cosmic ray that can reach the Earth from interstellar space?
 |
|---|