




 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
|||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
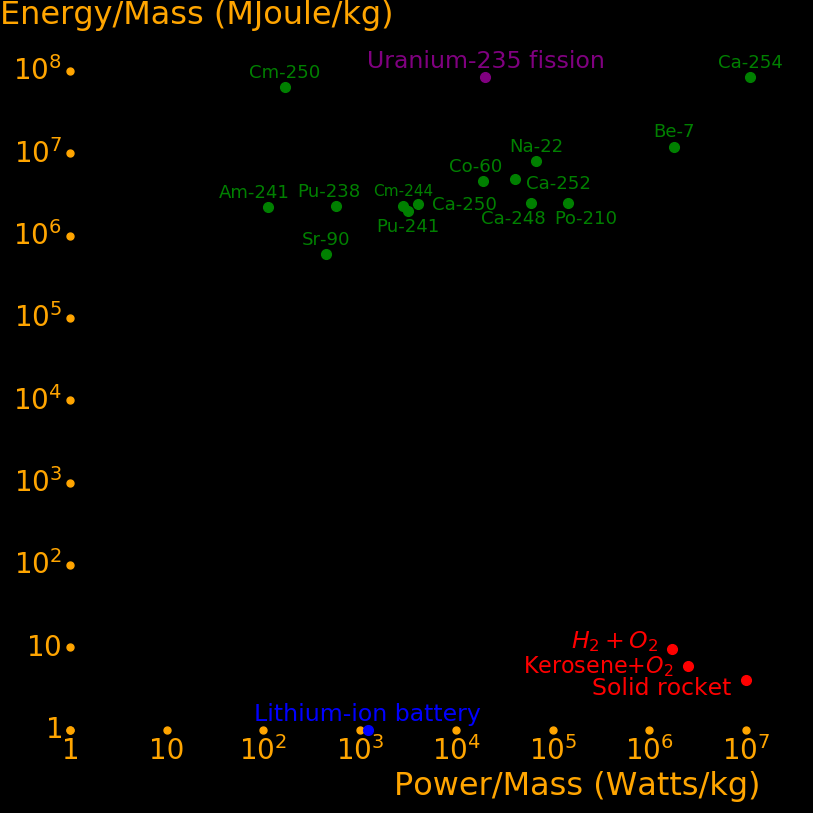
The rockets that are possible with current technology are:
Chemical React chemicals, for example hydrogen + oxygen Thermal hydrogen Hydrogen exhaust is heated with nuclear or solar power Ion rocket Accelerate ions, powered by electricity from nuclear or solar Fusion bomb rocket Can move large objects like asteroids Fission afterburner Neutrons trigger fission in the exhaust Alpha rocket A radioisotope emits alpha particles as exhaust
 |
|---|
Chemical H2+O2, Kerosene+O2, or solid fuel (Al+NH4NO3) Fission Uranium-235, Plutonium-239, Americium-242m, Beryllium-7 Radioactivity Plutonium-238, Cobalt-60, Lead-210 Solar Photovoltaic cells or solar mirror heat Fusion A fusion bomb using Deuterium + Lithium-6
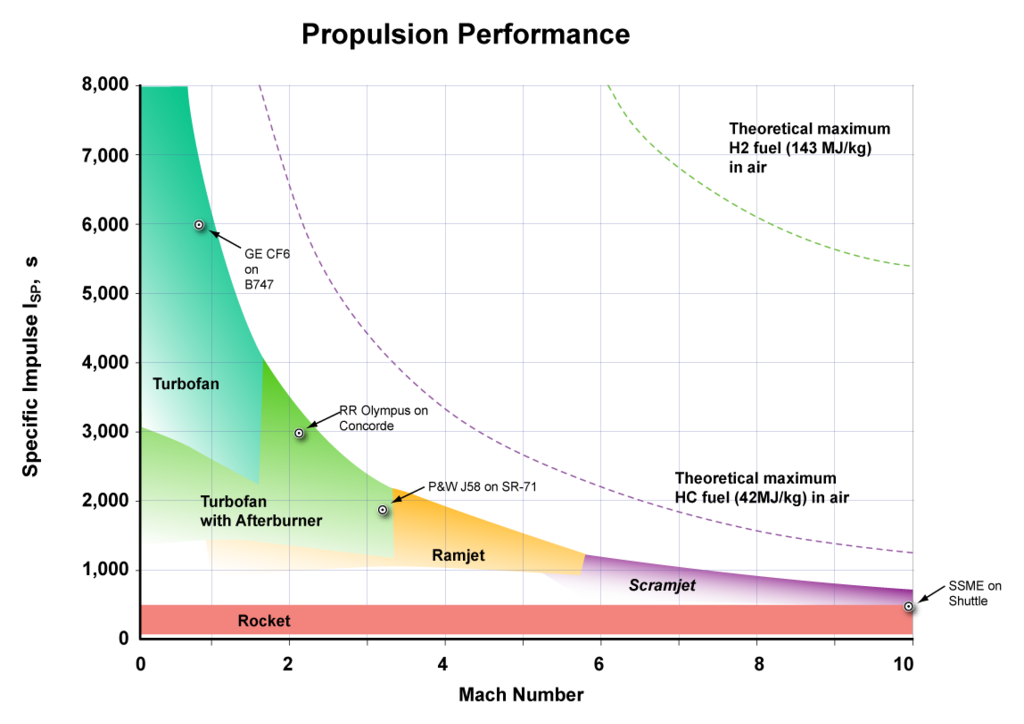
The maximum exhaust speed is given by the energy/mass of the energy source.
Exhaust speed = V Energy/Mass = e = ½ V2
This is the "perfect" exhaust speed. In practice the exhaust speed is less.
Energy Practical Perfect Energy/Mass
source exhaust exhaust
speed speed
km/s km/s MJoule/kg
Fusion Deuterium+Li6 6900 23000 270000000
Fission Uranium-235 4000 12000 74000000
Fission Plutonium-239 4000 12000 76000000
Radioactive Plutonium-238 50 2100 2300000
Chemical Hydrogen+O2 4.4 5.1 13.2
Chemical Methane +O2 3.7 4.7 11.1
Chemical Kerosene+O2 3.3 4.5 10.3
Chemical Al+NH4NO3 2.7 3.7 6.9
 |
|---|
The relationship between rocket quantities is:
Exhaust speed = V Exhaust energy/mass = e = ½V2 Exhaust power/mass = p = ½V2/T = e/T Burn time = T Acceleration = A = 2p/V = V/T
"Burn time" is the time for a rocket to expel its own mass of propellant. The shorter the burn time the better.
For ion drives the exhaust speed is customizable. The power/mass is fixed and there is a tradeoff between exhaust speed and acceleration. In the table below we choose a burn time of 107 seconds (3 months) for ion rockets.
It is difficult to make a rocket with both large power/mass and large exhaust speed. Fusion bombs qualify but they can only be used to move large objects like asteroids.
Rocket type Exhaust Power/Mass Acceleration Burn time
km/s Watts/kg meters/s/s seconds
Chemical, Hydrogen+O2 4.4 1700000 770 5.6
Chemical, Methane +O2 3.7 2500000 1350 2.7
Chemical, Kerosene+O2 3.3 5000000 3030 1.1
Chemical, Al+NH4NO3 2.5 9000000 7200 .3 Solid fuel
Fission thermal H2 9 160000 36 253 A fission reactor heats H2
Fission thermal H 13 70000 11 1200 A fission reactor heats atomic hydrogen
Ion drive 45 100 .0045 10000000
Fission afterburner, Am-242m 93 200 .0043 22000000
Fission afterburner, Pu-239 30 200 .013 2200000
Fission afterburner, Be-7 134 200 .0030 45000000
Fission afterburner, He-3 40 200 .010 4000000
Fission afterburner, Li-6 31 200 .013 2400000
Fission afterburner, B-10 35 200 .011 3100000
Alpha, Po-210 77 171 .0016 12000000 Half life .38 years
Alpha, Ca-248 71 60 .002 28700000 Half life .91 years
Alpha, Ca-252 68 19 .00019 82000000 Half life 2.6 years
Alpha, Pb-210 77 2.9 .000075 730000000 Half life 22.3 years
Alpha, U-230 200 7000 Half life .0554 years
Alpha, Th-228 180 170 .0019 62000000 Half life 1.91 years
Alpha, Ra-228 180 57 .00063 190000000 Half life 5.75 years
Alpha, Ac-227 180 15 .00017 710000000 Half life 21.8 years
Alpha, U-232 200 5.7 Half life 68.9 years
Fission bomb Large Large Large Short
Fusion bomb Large Large Large Short Deuterium + Lithium-6
Solar sail 300000 228000 .00152
 |
 |
 |
 |
|
|---|---|---|---|---|
The chemical rocket with the fastest exhaust is hydrogen+oxygen (HOX). It is the most expensive chemical rocket because hydrogen has to be liquefied at 20 Kelvin. Because the liquid hydrogen has low density, HOX can't be used for the first stage of a ground rocket, but it can be used for upper stages. HOX is easy in space.
Kerosene is often used because it's liquid at room temperature. Methane is slightly better than kerosene but it must be stored as a liquid at 112 Kelvin.
Solid fuel is cheap, simple, and reliable, and is often used for the first stage.
Fuel Exhaust Fuel Fuel boiling
speed density point
(km/s) (g/cm3) (K)
Hydrogen 4.4 .07 20 Complex because of the low boiling point of hydrogen
Methane 3.7 .42 112 New technology pioneered by SpaceX
Kerosene 3.3 .80 410 Simple because kerosene is a liquid at room temperature
Solid fuel 2.7 1.2 - Simple and cheap. Often Aluminum + NH4NO3
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|
In air launch, an aircraft launches a rocket at high altitude. Air launch has advantages over ground launch, such as:
*) The aircraft speed adds to the rocket speed.
*) Less air drag. Air at 15 km has 1/4 the density of air at sea level.
*) The rocket can be launched at the equator so that the Earth's equatorial speed adds to the rocket speed.
*) Ramjet launch makes it possible to reach orbit with cheap solid rockets.
Speed Speed
(km/s) (Mach)
Earth rotation at equator .46 1.6
Turbofan aircraft .27 .9
Ramjet aircraft 1.5 5
Scramjet aircraft >1.5 >5
Solid rocket exhaust 2.7 9
Kerosene rocket exhaust 3.3 11
Hydrogen+Oxygen rocket exhaust 4.4 15
low Earth orbit 7.8 26.4
At present, turbofan aircraft are being built for launching rockets, and in the near future ramjet aircraft will be used. For ramjet launch:
Stage Type Speed increase End speed
km/s km/s
0 Equator motion .45 .45
1 Ramjet 1.55 2.0
2 Solid rocket 4.0 6.0
3 HOX 2.0 8.0 Orbit speed
 |
|---|
 |
 |
|---|---|
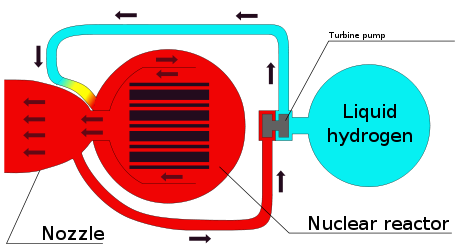
A fission thermal hydrogen rocket uses fission to heat hydrogen propellant. It has a higher exhaust speed than chemical rockets (13 km/s vs. 4 km/s).
In a chemical rocket the energy comes from a chemical reaction and this puts an upper limit on the exhaust speed. Reacting hydrogen and oxygen gives an exhaust speed of 4.4 km/s. Nuclear power can reach higher exhaust speed.
Rocket type Exhaust speed (km/s) Nuclear Fission thermal H 13 Nuclear Fission thermal H2 9 Chemical Hydrogen + Oxygen 4.4 Chemical Methane + Oxygen 3.7 Chemical Kerosene + Oxygen 3.3 Chemical Solid fuel 2.7
Hydrogen is used for its low mass. The lower the mass of the propellant molecule, the higher the exhaust speed.
Exhaust speed is determined by temperature. For a temperature of 2750 Kelvin, the speed of monatomic hydrogen propellant is 13 km/s.
Monatomic hydrogen mass= M =1.66⋅10-27 kg Temperature = T = 2750 Kelvin Exhaust speed = V = 13 km/s Boltzmann constant = k =1.38⋅10-23 Joules/Kelvin Exhaust constant = K = ½ M V2 / (1.5 k T) = 2.46
At 2750 Kelvin,
Molecule Mass Exhaust speed
AMU km/s
H 1 13.0
H2 2 9.2
H2O 18 3.1
H2 dissociates into atomic H at high temperature and low density. A thermal rocket has two modes: use H2, which has high pressure and high power/mass, or use H, which has low pressure and low power/mass. The low-pressure mode still has enough power/mass to propel humans to the outer planets.
In a mirror rocket, a space mirror focuses sunlight onto hydrogen propellant.
The fission material with the highest melting point is uranium oxide, which melts at 3138 Kelvin. Achieving a higher temperature requires liquid fission fuel that's embedded in a material with a higher melting point. The materials with the highest melting points are:
Melt Boil
Kelvin Kelvin
HfCN 4400
Ta4HfC5 4263
Hafnium carbide HfC 4201
Tantalum carbide TaC 4150
Niobium carbide NbC 3881
Zirconium carbide ZrC 3805 5370
Carbon (graphite) 3800
Tungsten 3695 6203
 |
|---|
A thin film mirror can focus sunlight and heat hydrogen. The power/mass of the rocket is limited by the power/mass of the mirror. JPL designed a mirror with the goal of minimizing mass/area.
Solar flux = f = 1365 Watts/meter2 Mirror mass/area = d = .006 kg/meter2 Mirror power/mass = p = f/d =228000 Watts/kg
The mirror consists of mylar coated with aluminum.
Mylar density = 1.39 g/cm3 Aluminum density = 2.70 g/cm3 Mylar thickness = .025 mm Aluminum thickness = .010 mm
 |
|---|
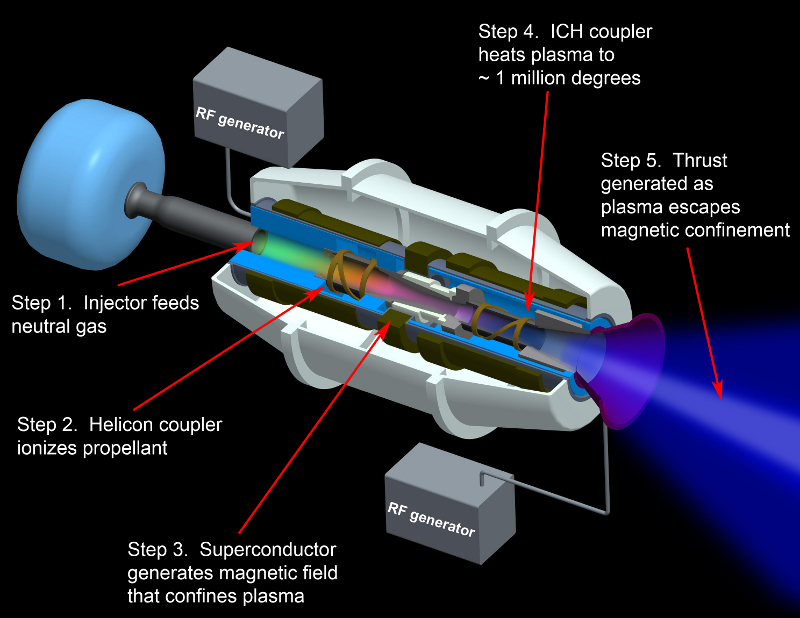
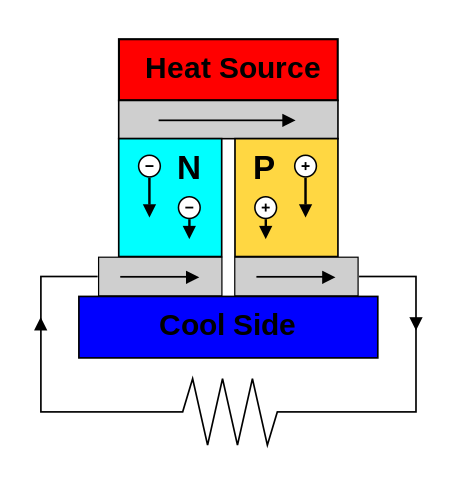
An ion drive uses electric power to accelerate ions. Electric power can come from nuclear fission, radioactivity, or solar cells. The ion speed is customizable. It should be at least as large as 20 km/s otherwise you might as well use a chemical or thermal rocket. The upper limit is given by the mission duration. We calculate the ion speed assuming a Plutonium-238 heat source and a burn time of 107 seconds.
Heat source Power/Mass = P = 567 Watts/kg Plutonium-238 Electrical efficiency = D = .05 Convert heat to electricity Drive efficiency = d = .6 Convert electricity to ion energy Electric Power/Mass = p = edP = 28 Watts/kg Burn time = T = 10 Million seconds = 3 months Ion speed = V = (2pT)½ = 24 km/s Ion Energy/Mass = e = pT = 280 MJoules/kg
Power in space is usually limited by cooling. For an electric generator that is closed-cycle and doesn't expel mass, cooling is limited by blackbody radiation and the maximum power/mass is determined by temperature. An example of an open-cycle system is a thermal hydrogen rocket, where the expelled mass serves as coolant and the power/mass can be much higher than for a closed-cycle system.
 |
|---|
The power/mass of solar cells depends on distance from the sun. At the Earth, solar cells have similar power/mass as nuclear, and beyond the Earth, solar cells are worse than nuclear.
Location Power/Mass Distance from sun
Watts/kg AU
Earth 100 1
Mars 43 1.52
Ceres 13 2.77
Jupiter 3.7 5.2
 |
 |
 |
 |
|---|---|---|---|
Heat can be converted to electricity with a Stirling engine, a thermoelectric generator, or photovoltaics. Usually the generator and cooling system have more mass than the heat source. Heat comes from fission or radioactivity.
Examples of existing space generators:
Heat source Generator Electricity Heat source Electric Fuel Total
Watts/kg Watts/kg efficiency fraction efficiency
Uranium-235 Brayton 195 .25 SAFE-400 reactor
Uranium-235 Stirling 44 991 .23 .193 .044 Kilopower reactor
Plutonium-238 Thermoelectric 5.3 567 .068 .137 .0093 GPHS-RTG. Galileo and Cassini
Plutonium-238 Thermoelectric 4.2 567 .062 .119 .0074 Voyager 1 and Voyager 2
Plutonium-238 Thermoelectric 2.8 567 .049 MMRTG. Curiosity rover
Features of the Kilopower reactor:
*) Fuel cast as Uranium-Molybdenum alloy. Molybdenum has a melting point of 2896 Kelvin.
*) Beryllium oxide moderator, which has a melting point of 2780 Kelvin.
*) Boron carbide control rods, with a melting point of 3036 Kelvin.
*) Passive cooling with liquid sodium coolant, which melts at 371 Kelvin and boils at 1156 Kelvin.
*) Cannot melt down because the reaction rate decreases with increasing temperature.
*) Stirling engine to convert heat to electricity.
 |
 |
|---|---|
 |
 |
|---|---|
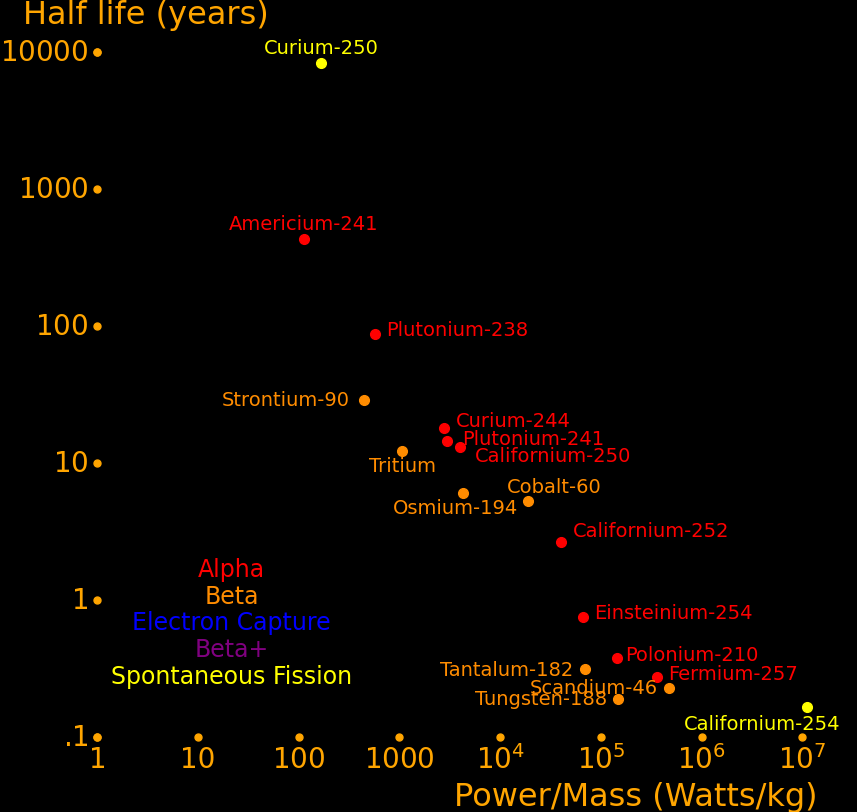
The most important radioactive isotopes for power are:
Plutonium-241 Good balance of power/mass and half life. Easy to produce. Curium-244 Good balance of power/mass and half life. Strontium-90 Abundant because it's present in burnt fission fuel. Polonium-210 Alpha rocket Lead-210 Alpha rocket Thorium-228 Alpha rocket Caesium-137 Abundant because it's present in burnt fission fuel. Plutonium-238 Outperforms Strontium-90. Has to be bred in a reactor. Cobalt-60 Larger power/mass than plutonium-238. Easily produced with neutron transmutation. Scandium-46 Ludicrously high power/mass, and easily produced by neutron transmutation. Californium-252 Superlatively large power/mass. Capable of powering an Iron Man suit. Curium-252 Decays by spontaneous fission 3% of the time Curium-254 Decays primarily by spontaneous fission
Half life Heat Decay Decay Obtainable by
year Watt/kg MeV neutron transmutation
Californium-254 .166 11200000 Fission 207 *
Scandium-46 .229 485000 β 2.366 *
Polonium-210 .379 144000 α 5.41 *
Ruthenium-106 1.023 71200 2β 3.584 *
Californium-252 2.64 41400 α or Fission 12.33 * α 96.9% (6.12 Mev). Fission 3.09% (207 MeV)
Cobalt-60 5.27 19300 β 2.82 *
Osmium-194 6.02 4313 2β 2.330 *
Lead-210 22.3 2907 α 9.100 *
Plutonium-238 87.7 578 α 5.59 *
Americium-242m 141 725 2α 12.33 *
Curium-250 8300 170 Fission 148 * Fission 74%, Alpha 18%, Beta 8%
Beryllium-7 .146 1822000 EC .547
Sodium-22 2.6 68700 β+ or EC 2.842
Uranium-230 .0554 9280000 6α+2&beta
Thorium-228 1.912 235000 5α+2&beta 34.784
Radium-228 5.75 90660 5α+4&beta 40.198
Polonium-208 2.898 α
Actinium-227 21.8 21600 5α+3&beta 36.18
Uranium-232 68.9 7545 6α+2&beta 40.79
Radium-226 1599 286 5α+4&betz 34.958
Thorium-229 7917 57.7 5α+3&beta 35.366
Protactinium-231 32600 16.2 6α+3&beta 41.3
For a heat engine, the higher the temperature, the more efficient. High temperature also means higher radiative cooling power. Isotopes with a high boiling point are:
Half life Heat Decay Decay energy Melt Boil Obtainable by
year Watt/kg MeV Kelvin Kelvin neutron transmutation
Uranium-230 .0554 9280000 6α 1405 4404
Tungsten-188 .191 148700 2Beta 3695 6203 *
Tantalum-182 .313 68866 Beta 3290 5731 *
Tungsten-181 .332 59200 EC 1.732 3695 6203 *
Iridium-194m .468 50400 Gamma 2.229 2719 4403 *
Rhodium-102 .557 67000 Beta+ 2237 3968
Ruthenium-106 1.023 71200 2Beta 3.584 2607 4423 *
Hafnium-172 1.87 11700 EC 1.835 2506 4876
Thorium-228 1.912 235000 5α 34.784 2023 5061
Rhodium-101 4.07 9890 EC 1.980 2237 3968
Osmium-194 6.02 4313 2Beta 2.33 3306 5285 *
Actinium-227 21.8 12000 5α 36.18 1500 3500
Uranium-232 68.9 7545 6α 40.79 1405 4404
Thorium-229 7917 57.7 5α+3&beta 35.366 2023 5061
Protactinium-231 32600 16.2 6α+3&beta 41.33 1841 4300
 |
|---|
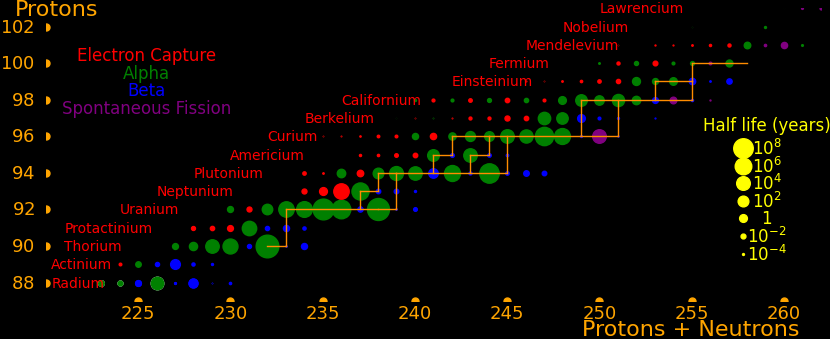
Neutron capture transmutes an isotope one space to the right and beta decay transmutes an isotope one space up.
The most massive nuclei that exist naturally are thorium-232, uranium-235, or uranium-238. All are unstable but have half lives larger than 700 million years. The road starts with these isotopes and then adding neutrons transmutes them according to the orange lines. The road forks at beta isotopes, which can either beta decay or capture a neutron.
The end of the road is fermium. Neutrons can't further increase the proton number because no fermium isotopes on the road beta decay. The road goes as far as fermium-258, which has a half life of .00037 seconds and spontaneously fissions. Producing heavier isotopes requires an accelerator or an extreme neutron flux (such as occurs in a fission bomb).
.svg.png) |
|
|---|---|
A TRIGA reactor doesn't melt down if the cooling system fails because it's engineered to turn off if it overheats. It's also designed so that adding and removing fuel elements is easy. The reactor is easy to build and can be operated in space.
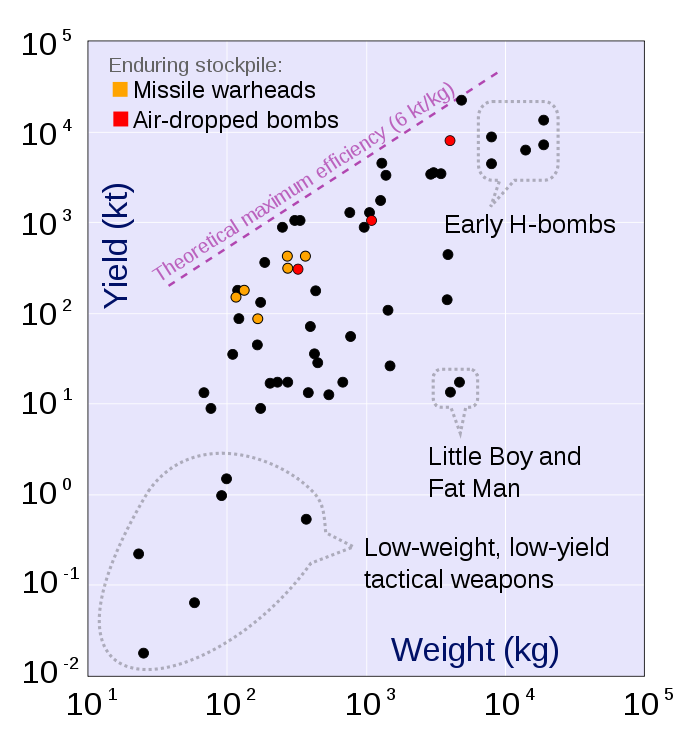 |
|---|
Fusion bomb maximum practical yield = = e = 21700 GJoules/kg Mass fraction converted to energy = f = e/C2 =.00072 Exhaust speed = V = (2e)½ = 6588 km/s
Mass is usually added to the bomb to increase momentum and decrease exhaust speed. Or, the bomb is detonated underground in an asteroid, which adds mass.
 |
 |
|---|---|
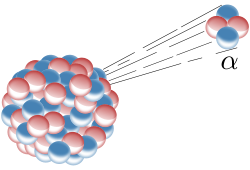
Alpha particles can be used as exhaust. An alpha emitter is coated on a mylar sail, with the coating thin enough so that most of the alphas escape into space. This rocket is simple and can be made arbitrarily small.
The recoil momentum of the nucleus is absorbed by the sail and the recoil speed of the nucleus is the effective exhaust speed. For example, polonium-208 alpha decays to lead-204 and the recoil speed of lead-204 is:
Alpha mass = m = 4 AMU = 6.64⋅10-27 kg lead-204 mass = M = 204 AMU Alpha energy = e = ½ m v2 = 5.22 MeV The alpha gets almost all the kinetic energy Alpha speed = v = (2e/m)½=15871 km/s lead-204 recoil speed = V = vm/M = 311 km/s
The speed calculated is for the most fortunate case where the alpha goes directly aft of the spacecraft. Calculating the average recoil speed involves integrating over all emission directions and accounting for absorption by the emitting material. In the ideal case, all particles emitted in the aft hemisphere escape and all particles emitted in the forward hemisphere are absorbed, in which case the effective recoil speed is 1/4 the fortunate speed. For polonium-208 the effective recoil speed is 78 km/s.
To calculate the power/mass of an alpha rocket,
Speed of projectile = v Speed of emitter (recoil) = V Mass of projectile = m = 4 AMU Mass of emitter = M = 204 AMU Energy of projectile = e = ½mv2 Energy of emitter = E = ½MV2 Momentum of projectile = q Perfect exhaust speed = S = q/M Effective exhaust speed = s = S/4 Effective exhaust energy = g = ½Ms2 Exhaust energy / Decay energy = r = g/e = 16-1 m/M
For a polonium-208 alpha rocket, the power/mass and energy/mass are:
Effective recoil speed = V = 78 km/s Energy/Mass = e = ½V2 =3042 MJoules/kg Half life = T =2.90 years Power/Mass = p = e/t = 33 Watts/kg
The lighter the isotope the larger the recoil speed. Almost all alpha emitters are actinides, the only exceptions being gadolinium-148, polonium-208, polonium-209, and polonium-210. Alpha rockets using actinides have an average recoil speed of ~75 km/s.
The best alpha-emitting isotopes are:
Half life Power/Mass Decay Energy Neutron transmutable
year Watts/kg MeV
Polonium-210 .379 144000 α 5.41 *
Einsteinium-254 .755 105432 α 6.616 *
Californium-248 .91 59760 α 6.36
Californium-252 2.64 21640 α 6.12 *
Polonium-208 2.898 α
Californium-250 13.1 5779 α 6.02 *
Curium-244 18.1 4014 α 5.80 *
Curium-243 29.1 1885 α
Lead-210 22.3 2907 α 9.100 *
Gadolinium-148 70.9 952 α 3.18
Plutonium-238 87.7 578 α 5.59 *
Americium-242m 141 725 2α 12.33 *
Thorium-227 .0512 9194000 6α+2β 36.14
Uranium-230 .0554 9280000 6α+2β
Thorium-228 1.912 235000 5α+2β 34.784
Radium-228 5.75 90660 5α+4β 40.198
Actinium-227 21.8 21600 5α+3β 36.18
Uranium-232 68.9 7545 6α+2β 40.79
Radium-226 1599 286 5α+4β 34.958
Thorium-229 7917 57.7 5α+3β 35.366
Protactinium-231 32600 16.2 6α+3β 41.33
A charged particle passing through matter loses energy from collisions with electrons, with the energy loss rate given by the Bethe formula. For an alpha particle passing through water,
Particle energy = E = 6 MeV Particle mass = M = 4 AMU Particle charge = Z = 2 Proton charges Material density = D = 1000 g/cm2 Stopping distance = X = EZ-2M-1D-1C = .049 meters (Inputs in MeV, AMU, and g/cm3. Output in meters) Material stopping constant = C =.000131 Stopping power = S = 778000 MeV meter2 Mass/Area = m = DX = .049 kg/meter2
 |
|---|
Sea level Vacuum Thrust
Fuel Exhaust Exhaust Mass Thrust /mass
km/s km/s kg kN N/kg
Waxwing Solid 2.72 87 29.4 345
Atlas V Solid 2.70 1270 40.8 tons with fuel
P230 Solid 2.80 6472 268 tons with fuel. Ariane rocket
Shuttle booster Solid 2.42 2.68 12500 21200 590 tons with fuel
Merlin 1D Kerosine 2.76 3.05 630 801 1300 Falcon rocket. Diameter 1.676 m
Merlin 2 Kerosine 3.16 8540 In development by SpaceX. Falcon Heavy
Raptor Methane 3.7 8200 In development by SpaceX
Snecma HM7B HOX 4.3 165 64.8 400 Ariane rocket
RL-10A HOX 4.42 167 99.1 606 Atlas V. Diameter = 2.13 meters
RL10B-2 HOX 4.547 277 110 406 Atlas V and Delta IV rockets
Mitsubishi LE-5B HOX 4.38 285 137.2 490
Mitsubishi LE-7A HOX 4.31 1800 1098 620
Vulcain 2 HOX 4.20 1800 1359 755 Ariane rocket. Diameter = 1.76 m
Shuttle engine HOX 3.56 4.44 3500 1700 496
RS-68 HOX 4.02 6600 3370 520 Most powerful HOX rocket
HOX = liquid hydrogan + liquid oxygen
Kerosine = kerosine + liquid oxygen
Solid = aluminum + ammonium perchlorate (N H4 Cl O4)
Methane = methane + liquid oxygen
Mass Thrust Payload Payload
kkg MN kkg $/kg
Space Shuttle 1710 25 93.
SpaceX Falcon 9 506 6.67 13.15 4109
SpaceX Falcon Heavy 1421 22.8 63.8 2350
Saturn V 2800 34 118 9915
Ariane 777 12.9 16 10500
Pegasus 23.1 .443
Stratolaunch ? 1.5 6.12
 |
.jpg) |
 |
|---|---|---|
 |
 |
 |
|---|---|---|
Stage 1 Stage 2 Stage 3
Mass Thrust Exh Mass Thrust Exh Mass Thrust Exh Payload Payload
kkg kN km/s kkg kN km/s kkg kN km/s kkg $/kg
Space Shuttle 1710 25000 ~2.6 530 5100 4.44 ? 5100 4.44 93.
SpaceX Falcon 9 506 6672 ~2.9 52 801 3.35 - - - 13.15 4109
SpaceX Falcon Heavy 1421 17000 ~2.9 ~480 5600 3.05 ? 445 3.35 53. 2200
Saturn V 2800 34000 2.58 710 4400 4.13 230 1000 4.13 118.00 9915
Ariane 777 12940 2.80 ? 1340 4.22 ? 64.7 4.37 16. 10500
Pegasus 23.1 .443
Stratolaunch ? 1500 n/a 230 ? ? ? ? ? 6.12
Earth rotation at equator = 463 m/s.
Earth escape speed = 11.186
Earth orbit speed at 160 km = 7.58 km/s
Falcon 9 stage 2 empty mass = 3.1 tons
Falcon 9 Sea level thrust = 5885 kN
Space shuttle: The space shuttle orbiter has a mass of 68.6 and a payload of 24.4 tons.
Saturn V: Largest payload ever achieved. Launched the moon missions.
Pegasus: Air launch
Stratolaunch: A 6-engine airplane launches the "Pegasus II" rocket.
The Stratolaunch airplane is moving at ~ .3 km/s when it launches the
rocket, and the launch can occur at the equator where the Earth's rotation
speed is .46 km/s. This gives the rocket a total initial speed of .76 km/s.
 |
 |
|---|---|
Engine Engine Empty Max Cargo
Speed Ceiling thrust mass mass takeoff mass
(Mach) km (tons) (tons) (tons) (tons) (tons)
Blackbird SR-71 3.3 25.9 2 x 14.8 2 x 2.7 30.6 78 Spy
F-15 Eagle 2.5 20.0 2 x 11.3 2 x 1.70 12.7 30.8 Fighter
F-22 Raptor 2.25 19.8 2 x 15.9 2 x 1.77 19.7 38 Stealth Fighter
Concorde 2.02 18.3 4 x 17.2 4 x 3.18 78.7 187 128 passengers
Airbus A380 .96 13.1 4 x 38.2 4 x 6.27 276.8 650 853 passengers
Boeing C-5 Galaxy .8 4 x 19.4 4 x 3.63 172.4 381 122.5 Cargo
Boeing 747-8F .86 13.0 4 x 30.2 4 x 5.6 448 134.2 Cargo
Antonov 224 .75 4 x 23.4 4 x 4.1 175 405 150 Cargo
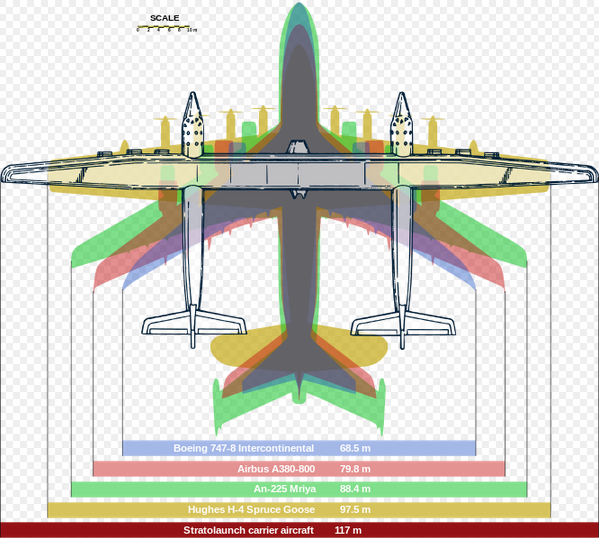
Antonov 225 .7 6 x 23.4 6 x 4.1 285 640 250 Cargo
Stratolaunch 6 x 25.5 540 230 Orbital launch platform
The Stratolaunch (in development) is designed to launch rockets into space.
Drag force = .5 * AirDensity * CrossSection * Velocity^2 M = Rocket Mass / 400 tons A = Acceleration / 10 m/s^2 Acceleration in units of g's D = Air Density / 1 kg/m^3 Density = 1.28 kg/m^3 at sea level C = Cross section / 10 m^2 The Falcon 9 rocket has a cross section of 10 m^2 V = Velocity / 300 m/s Velocity in units of "Mach"In these units the drag equation is
10 A M ~ D C V^2 For a falcon 9 rocket, M=1 and C=1. If the rocket is at sea level, D ~ 1.If the drag acceleration is 1g, then V ~ 3 (Mach 3). This sets the speed limit for rockets in the lower atmosphere.
Fuel Exhaust Density Boil kNewtons kNewtons kNewtons Diameter Mass Rocket engine used
(km/s) (g/cm^3) (K) /meter^2 /ton (meters) (kg) for data
Liquid hydrogen 4.2 .07 20.3 559 755 1359 1.76 1800 Vulcain-2
Liquid methane 3.7 .42 111.7 493 ? 8200 4.6 ? Raptor
Kerosine 3.3 .80 410 361 1270 801 1.676 630 Merlin-1D
Solid fuel 2.7 1.2 - 673 ? 1270 1.55 ? Atlas V booster
Kerosine ramjet .80 410 9.0 5.5 14.8 1.45 2.7 SR-71 Blackbird
Hydrogen, methane, and kerosine are all reacted with liquid oxygen that is
carried by the rocket. Solid fuel contains its own oxidizer.
For the kerosine ramjet, kerosine is reacted with oxygen from the air.
"kNewtons/meter^2" is the thrust/area of the rocket.
"kNewtons/kg" is the thrust-to-mass ratio of the rocket engine.
The density of liquid oxygen is 1.14 g/cm^3 and the boiling point is 90.2 Kelvin.
Electricity can split H2O into H2 and O2, which can be used for rocket fuel. the maximum efficiency of this process is 0.83.
Energy to split H2O into H2 and O2 = E = 1.317e7 Joules/kg Max efficiency to split H2O into H2 and O2 = e = .83 Solar cell power per mass = Sp = 300 Watts/kg Solar cost per mass = Sc = 3000 $/kg Time for a 1 kg solar cell to form 1 kg of fuel = T = .61 days = E / e / Sp
We can calculate the maximum speed of HOX rocket exhaust from the energy required to split H2O.
V = Maximum speed of rocket exhaust for a HOX rocket 1.317e7 Joules/kg = ½ V2 V = 5.132 km/sIn practice, the best HOX rockets have an exhaust speed of 4.4 km/s.
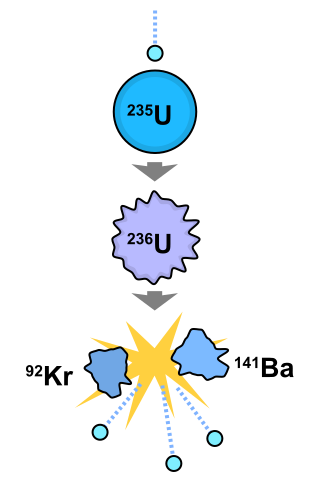
Mean energies for the fission of Uranium-235, in MeV:
Fission fragment kinetic energy 169.1
Prompt neutrons 4.8
Prompt gamma rays 7.0
Delayed beta rays 6.5
Delayed gamma rays 6.3
Captured neutrons 8.8
Total energy generated as heat 202.5
Prompt antineutrinos 8.8
Total energy including antineutrinos 211.3
Energy of the original U-235 nucleus 218900
1 MeV = 10^6 eV = 1.6*10^-13 Joules
1 Atomic mass unit = 1.6605*10^-27 kg = 931.494 MeV/C^2
Mass of Uranium-235 = 235.04 atomic mass units
Only the kinetic energy of the fission fragments is harnessable by a rocket.
C = Speed of light
Mt= Mass of original nucleus
E = Kinetic energy of the fission fragments
F = Fraction of the mass of the original nucleus that is
converted into kinetic energy.
= E / (Mt C^2)
= 169 MeV / (235.04 * 931.49)
= .000772
Vt= Characteristic speed of the fission fragments
.5 Mt Vt^2 ~ F Mt C^2
Vt = .0393 C
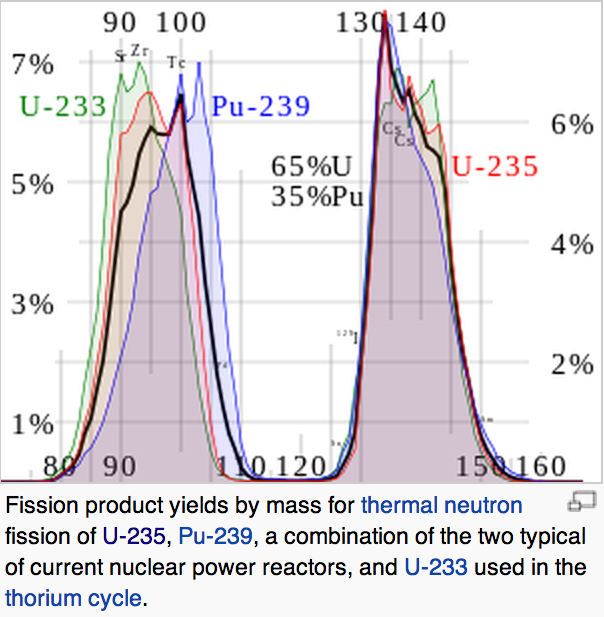 |
|---|
Fission tends to produce two fragments, one heavier than the other. The distribution is similar for all fissionable nuclei.
E = Total kinetic energy in fission fragments ~ 169 MeV
F = Fraction of the mass of the original nucleus that is converted into kinetic energy.
= .000772
M = Mass of heavy fragment ~ .40 * Mass of original nucleus
m = Mass of light fragment ~ .58 * Mass of original nucleus
V = Velocity of heavy fragment
v = Velocity of light fragment
Conservation of momentum: M V = m v
Conservation of energy: E = .5 M V^2 + .5 m v^2
M^2 V^2 (M + m) = 2 E M m
V^2 = 2 F C^2 m / M
v^2 = 2 F C^2 M / m
V = .0326 C
v = .0473 C
Critical mass Half life
Americium-242 .5 141 years Costs ~ 10^6 $/kg
Californium-251 .9 898 years
Curium-245 1.1 8500 years
Plutonium-239 5.6 241000 years
Uranium-235 11.0 704 million years
For a fission fragment rocket, the lower the critical mass the better.
All of the above isotopes produce similar energy when fissioned.
Hydrogen bombs use the following reactions.
Neutron + Lithium6 -> Tritium + Helium4 + 4.874 MeV Deuterium + Tritium -> Helium4 + Neutron + 17.56 MeVLeaving out the neutron catalyst, this is
Deuterium + Lithium6 -> Helium4 + Helium4 + 22.43 MeV
Nucleons = 8
Energy / Nucleon = 22.434/8
= 2.80 MeV/Nucleon
f = Fraction of mass converted to energy
= (2.80 MeV/Nucleon) / (939 MeV/Nucleon)
= .00298
The theoretical limit for the efficiency of a hydrogen bomb is
f = .00027In practice, f is half this.
A thermal rocket uses a power source to heat the propellant. The power can come from either a nuclear reactor or from sunlight focused by mirrors.
Propellant Exhaust speed
(km/s)
H2 9
H2O 1.9
Energy
Hydrogen + Oxygen 1.4e10 Joules/ton
Uranium-235 8.0e16 Joules/ton
Solar energy 1.4e15 Joules. 1 km^2 collector operating for 10^6 seconds at 1 A.U.
A mirror-based thermal rocket offers a means for using H2O as propellant. Such a
rocket can potentially move large asteroids.
The solar energy collected by a 1km mirror at 1 A.U. over a time of 10^6 seconds (2 weeks) is
Energy ~ 1400 Watts/m^2 * 10^6 m^3 * 10^6 seconds ~ 1.4e15The mass of the mirror is
Surface area Thickness Density
Mirror mass ~ 8*10^5 kg -------------- ----------- ----------
1 km^2 10^-4 m 8 g/cm^3
A solar thermal rocket capable of delivering ~ 10^16 Watts can be built
from a ~ 10 meter metallic asteroid.
If a thermal rocket can operate at a temperature high enough to dissociate H2 into elemental hydrogen then larger exhaust speeds are possible.
Suppose we use mylar film for a space mirror.
Mirror density = 1390 kg/m^3 Mirror thickness = .1 mm Mirror mass/area = .139 kg/m^2 Solar flux = 1362 Watts/m^2 H2O exhaust speed = 1.9 km/s H2O mass/time/area = .00075 kg/s/m^2 Mass of propellant per time per area Mirror acceleration = 10.3 m/sThe acceleration of a mirror rocket is limited by the strength of the mirror.
If we assume that the kinetic energy of an orbiting object comes from electricity then
Orbital speed = 7.8 km/s Energy of a 1 kg object at orbital speed = 30.4 MJoules Cost of electricity = 36.0 MJoules/$ Cost of a 1 kg object at orbital speed = .84 $For a typical hydrogen+oxygen rocket, the mass fractions are:
Payload = 1 kg Superstructure = 2 kg Hyddrogen mass = 3 kg Oxygen mass = 24 kg Total mass = 30 kg Oxygen mass / Hydrogen mass = 8 Cost of liquid hydrogen = .70 $/kg Cost of liquid oxygen = .16 $/kg Cost of liquid hydrogen = 2.1 $ Cost of liquid oxygen = 3.8 $ Typical launch cost for 1 kg = 2500 $The superstructure is everything except the payload and the fuel.
Orbit speed = 7.8 km/s Energy of 1 kg at orbit speed = 30.4 MJoule Cost of electricity = .015 $/MJoule Electricity cost of the energy= .46 $
 |
|---|