





 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|
 |
 |
 |
 |
|---|---|---|---|
Astronauts can expect luxuriously large spaceships. The Bigelow BA-330 has as much room as the bridge of the Enterprise and the Bigelow Genesis has as much room as a Humvee. Bigelow habitats are lighter than NASA habitats and have thicker walls. Thicker walls are helpful for defending against micrometeorites and radiation.
Mass (tons) Volume (m3)
Bigelow BA-330 23 330
Bigelow Genesis 3 11
 |
 |
|---|---|
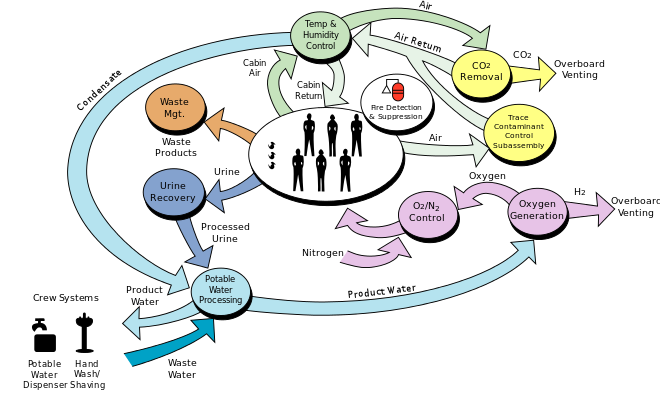
The space station life support system requires:
Power = 1 kWatt/person Water = 1 kg/person/day Food = 1 kg/person/day
 |
|---|