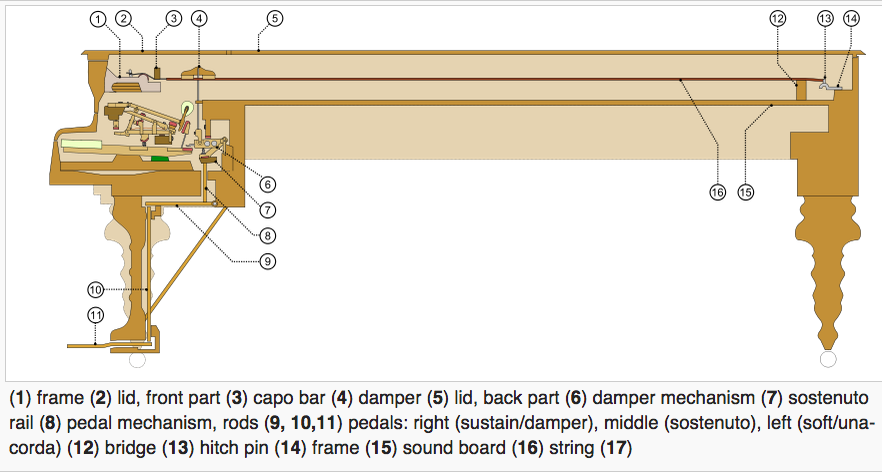
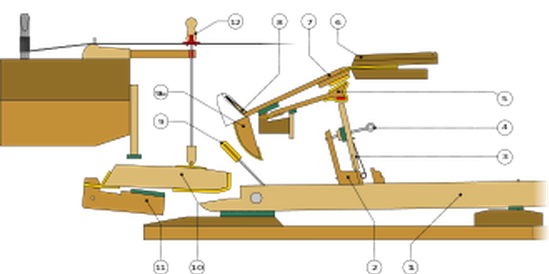
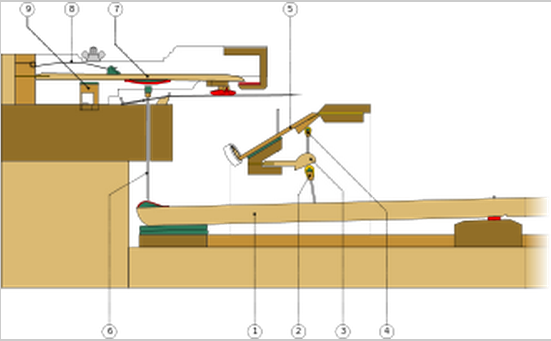
 |
|---|
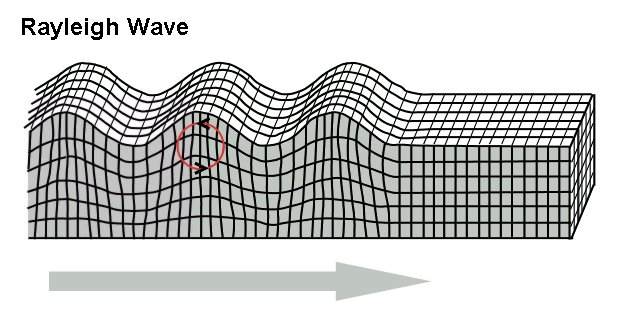
Mechanical waves require a medium to propagate. Sound waves can't propagate in the vacuum of space.
 |
 |
|---|---|
 |
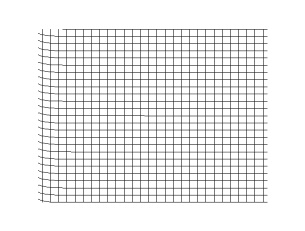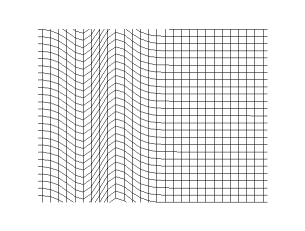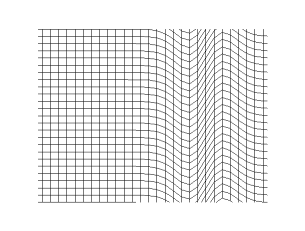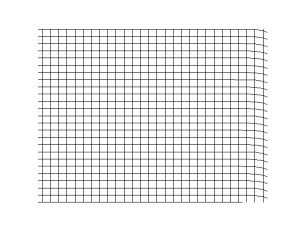 |
 |
 |
|---|---|---|---|
In rock, pressure waves propagate at ~ 5 km/s and shear waves propagate at ~ 3 km/s. You can estimate the distance from the center of an earthquake by measuring the time difference between the arrival of the pressure and shear waves.
 |
 |
 |
|---|---|---|
 |
 |
 |
|---|---|---|
 |
 |
 |
|---|---|---|
 |
 |
 |
|---|---|---|
 |
 |
 |
 |
|---|---|---|---|
 |
|---|
The Young's modulus characterizes the stiffness of a wire and it is proportional
to the spring constant.
Toughness is a measure of the maximum energy density that a material can absorb
before breaking. A tough material must be both strong and flexible.
Piano strings are "tough" in the sense that they are designed to absorb a large
strain before breaking. The tradeoff is that they cannot hold an edge.
Wootz steel is a steel-carbon alloy designed to be both strong and flexible.
The following table shows the maximum strain of a material before breaking.
Toughness is a measure of the maximum energy density that a material can absorb
before breaking. A tough material must be both strong and flexible.
The maximum energy/mass of a spring is proportional to the toughness/density.
Concrete and ceramics typically have much higher compressive strengths than
tensile strengths. Composite materials, such as glass fiber epoxy matrix
composite, tend to have higher tensile strengths than compressive strengths.
The deformation of a solid is characterized by shear strain, tensile strain,
and bulk compression.
Tensile strength relates to the strength of wires.
Shear strength relates to the strength of beams and columns.
The maximum force on a beam is determined by the shear strength.
If a column is short then it squashes before it buckles and if it is long then
it buckles before it squashes.
A column's resistance to squashing is determined by the Bulk strength.
If a material can be compressed indefinitely (until it turns into a neutron
star) then it has no concept of a "bulk strength". This applies especially to
metals and diamonds. Hence, the "bulk modulus" is usually the only meaningful
variable for compression.
A wire shortens when stretched and widens when compressed.
For an isotropic material the tensile, shear, and bulk moduli are related
through the dimensionless Poisson ratio.
The following figure characterizes the relation between the shear and tensile moduli.
The relationship applies well for most metals.
Previous to the discovery of tungsten, gold was an uncounterfeitable currency because
no material existed that was both more dense and less expensive than gold.
Osmium is the densest element and it is also expensive, making it useful as a currency.
Chromium is common in the Earth's crust and Ruthenium is rare.
For carbon, the values are given for diamond form.
Gold was the densest known element until the discovery of platinum in 1735.
This made it impossible to counterfeit as a currency.
Metals with a strength-to-weight ratio less than lead are not included, except
for mercury.
Corundum is a crystalline form of aluminium oxide (Al2O3). It is transparent in
its pure orm and can have different colors when metal impurities are
present. Specimens are called rubies if red, padparadscha if pink-orange, and
all other colors are called sapphire, e.g., "green sapphire" for a green
specimen.
Lignin comprises 30 percent of wood and it is the principal structural element.
A string ideally has both large strength and large strain, which favors
Vectran.
Below is a list of the elastic variables for a material, with examples for
large and small values for each variable.
Not all of of the above variables are independent. The toughness and
maximum strain are determined from the strength and modulus.
The most important variables for high-performance materials are
This table shows the elements with the highest melting points.
"Temperature" refers to the maximum temperature before the magnet loses its magnetism.
For a given instrument there is a characteristic ideal tension for the strings.
If the tension is too low or high the string becomes unplayable. The tension can
be varied to suit the performer's taste but it can't be changed by an extreme
degree.
The frequency of a string and the speed of a wave on the string are
related by:
The speed of a wave on a string is
The larger the radius the more difficult the string is to play and the more
impure the overtones. The radius can be minimized by using a material with a
high density. This is why cello, bass, and bass guitar strings are often made of
tungsten.
High-density strings are only appropriate for low-frequency strings because
they have a low wavespeed. High-frequency strings require a material with low
density.
String manufacturers almost never state the density and radius of the string.
You can infer the density from the type of metal used, with numbers given the
table below.
The speed of sound in air has an analogous form as the speed of a wave on a string.
If the tension force on a string exceeds the "Tensile strength" then the string
breaks.
A space elevator requires a material with Z > 100.
Gut was usually used in the Baroque age because steel alloys hadn't been
perfected. A-strings were tuned to a frequency of around 420 Hertz.
Modern steel made possible the 660 Hertz E-string and the high-frequency strings
on a piano.
You can use zylon to make a bass sound like a violin.
Tungsten is a high-density metal that can be used to make low-frequency strings
("Darth Vader" strings). You can make a violin sound like a bass.
The larger the diameter of a string the more difficult it is to play. Diameter
sets the lower limit of the frequency of a string.
If a string is made of tungsten with a density of 19.25 g/cm^3 then the
diameter of the lowest string on each instrument is
The "Tungsten" lines are string diameters for tungsten and the "Zylon" lines
are string diameters for zylon. Tungsten diameters assume a density of 19.3
g/cm^3 and zylon diameters assume a density of 1.5 g/cm^3. The zylon lines cut
off at the right at the frequency where the string breaks.
The price is for strings made of gold with a density 19.3 g/cm^3, the same
as for tungsten.
If the strings are made from iridium or osmium then the metal price is half this.
For tungsten strings the price of the tungsten is negligible.
Even though iridium is half the price of gold, gold wire may be cheaper because
gold is easier to forge.
When a beam is bent it exerts a restoring force. If a string is too stiff it
acts like a beam and becomes impossible to play. The stiffness is inversely
proportional to the Young's modulus. This is why metal strings are usually
wound around a flexible core.
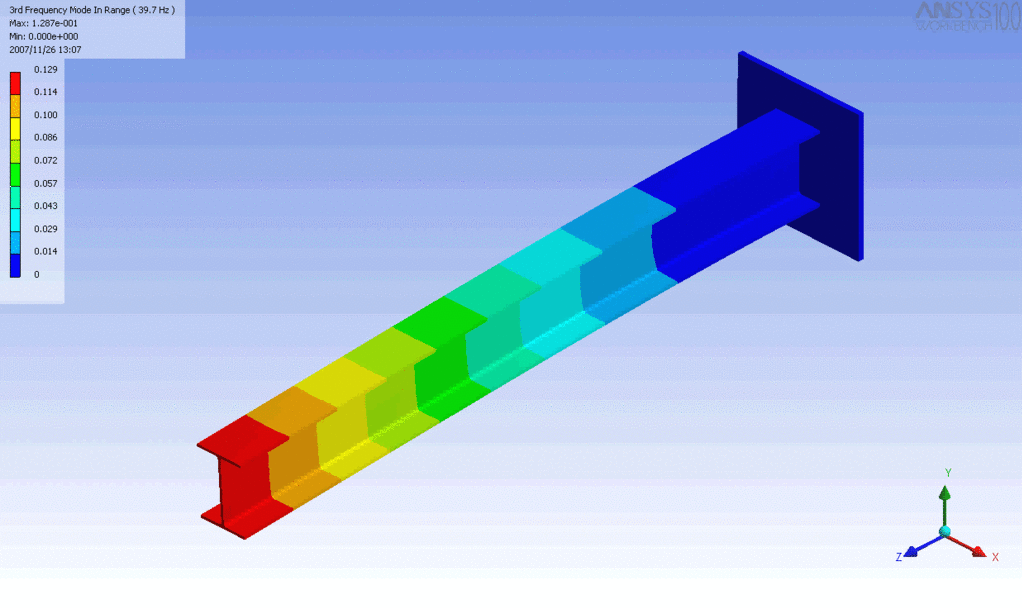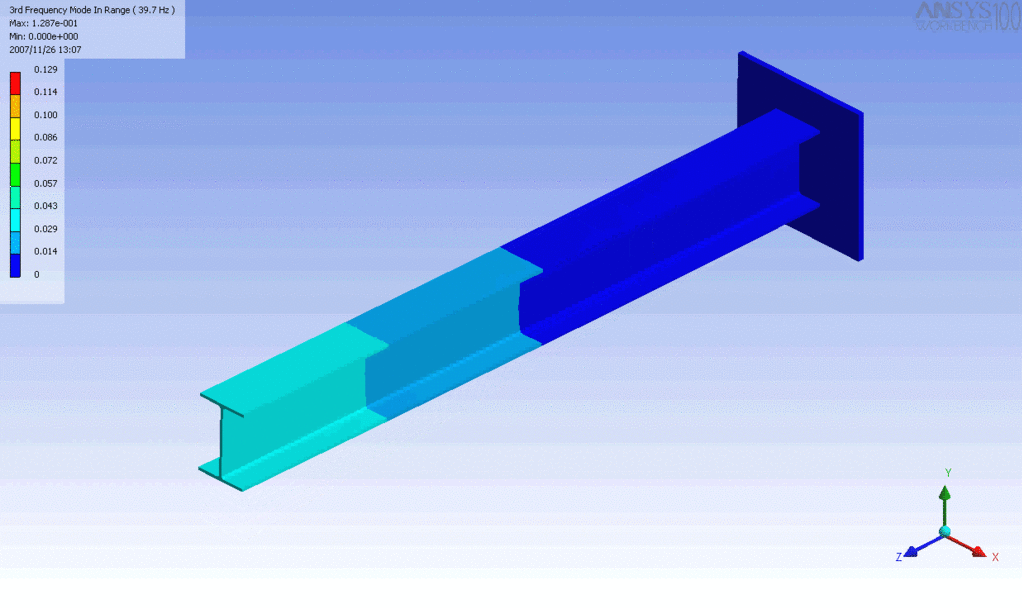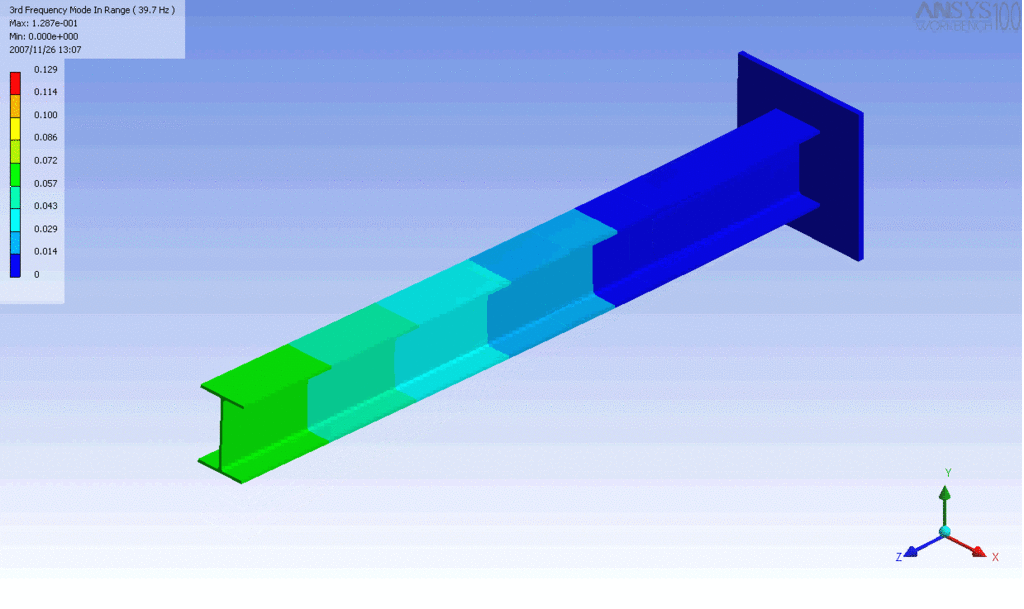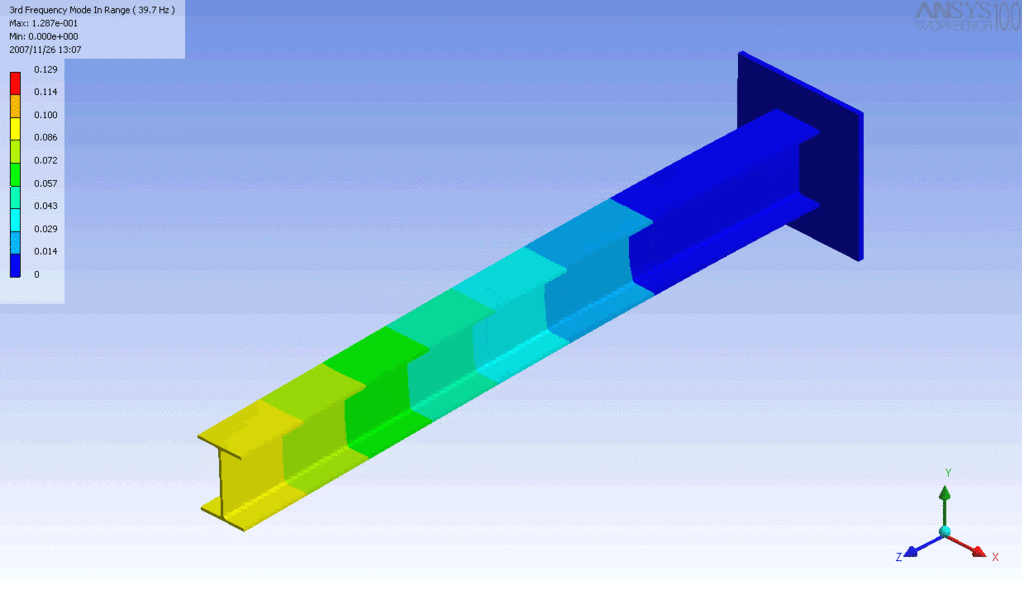
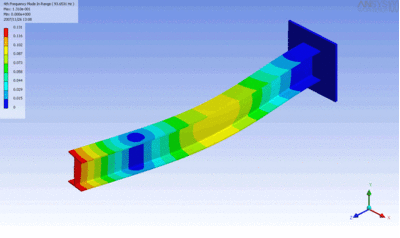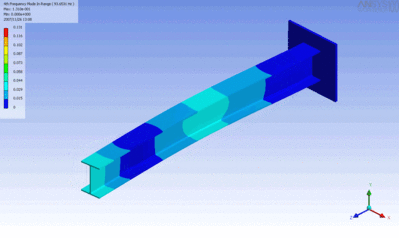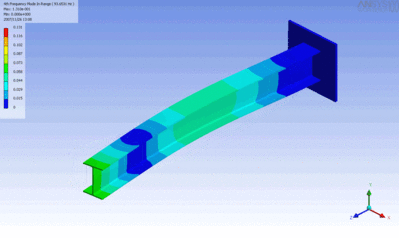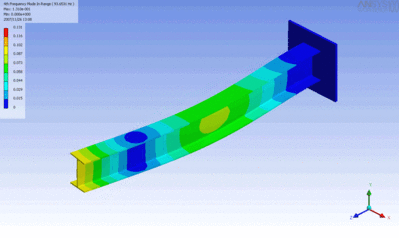
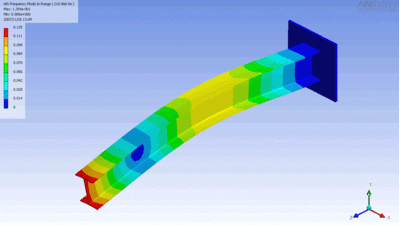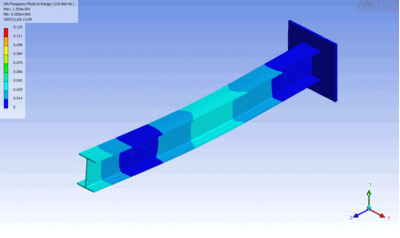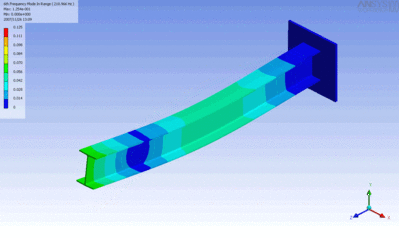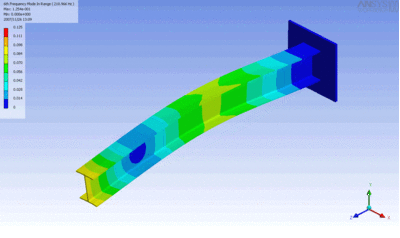
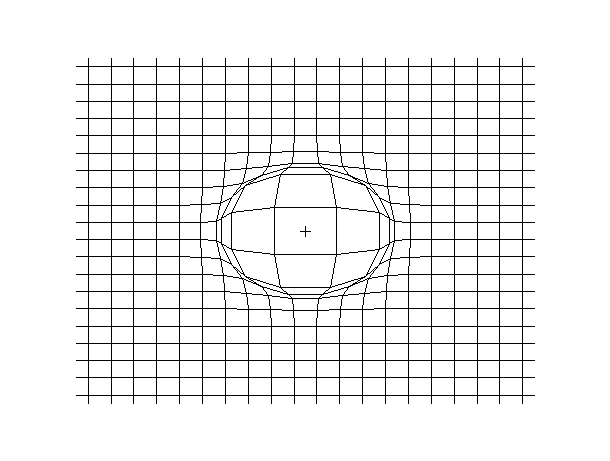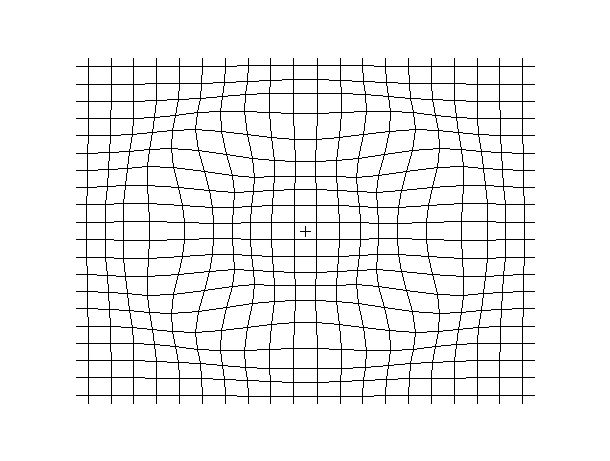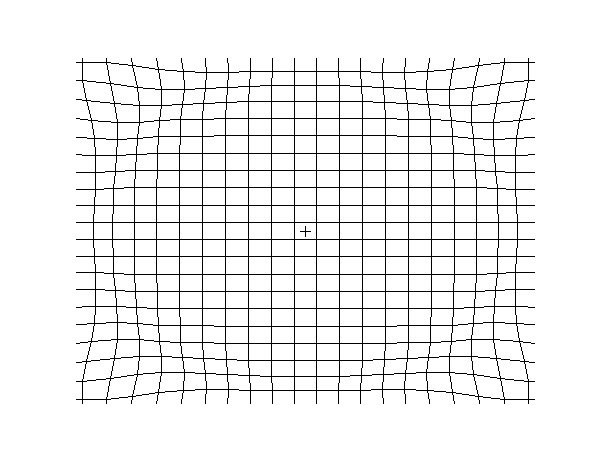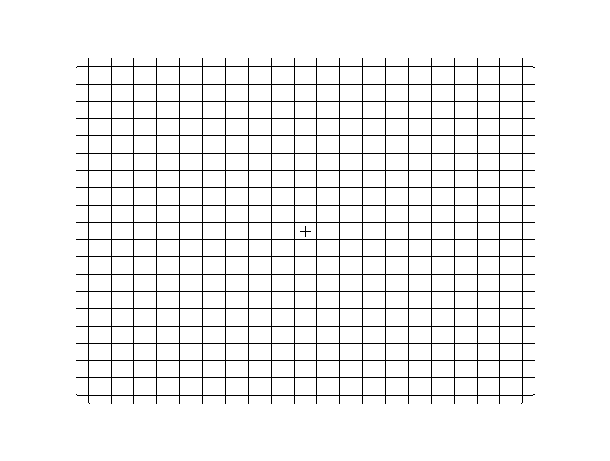
Examples of beam vibrations.
Strings typically have a flexible core with a low Young's modulus and a high-density
metallic winding.
The overtones of an ideal string are exact integer ratios.
If the string is non-ideal then the overtones can change.
The principal source of non-ideality is the finite thickness of the string.
String stiffness also contributes non-ideality.
Plucked strings exhibit inharmonicity. Bowed strings are "mode-locked" so that
the harmonics are exact integer ratios. Reed instruments and the human voice
are also mode locked.
The coefficient of inharmonicity can be expressed in terms of density as
Low strings are more inharmonic than high strings.
The higher the note you play on a string, the smaller the effective string length
and the more inharmonic the note. This is what prevents you from playing notes
of arbitrarily high frequency.
The following is a table of inharmonicity coefficients for various instruments.
We have assumed standard values for the string tension and we assume the string
has the density of steel.
The lower the frequency of a string, the more inharmonic it is. Low-frequency
strings typically consist of a synthetic core (for
elasticity) and an outer metallic winding (for density).
You can't use metal for the entire string because metal is too stiff (the Young's
modulus is too high.
An ideal core material has a high tensile strengh, so that you can use a small
core diameter, and a low Young's modulus, to minimize inharmonicity. The
synthetic material that is best suited for this is Vectran (see the table
above).
For constant string length the ideal force doesn't depend on frequency.
If "r" is too large compared to "R" then the string loses density. We assume that
r is is a fixed fraction of R and that r/R ~ 2/5.
Using
Let
The following table shows a set of example parameters for low-frequency strings.
We assume a core of Vectran (density=1400 kg/m^3) and a winding of
osmium (density=22600 kg/m^3).
The strings in a piano exert a force of 20 tons.
The Sydney Town Hall Grand Organ has pipes that are 64 feet long, which
corresponds to a frequency of 8.5 Hertz.
Developed theories of eye focus, depth perception, color vision, and motion perception.
Invented the "Helmholtz resonator" for measuring the frequency spectrum of sound.
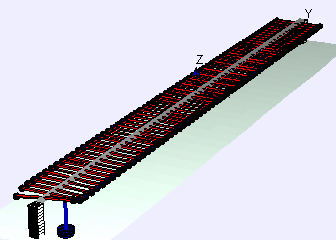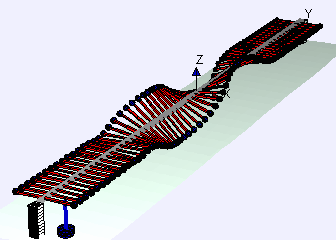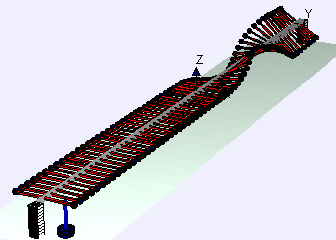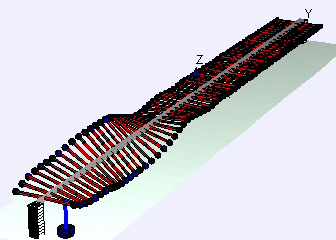
Discovered the shape of the oscillation of a violin string.
Demonstrated that different combinations of resonators could mimic vowel sounds.
Measured the speed of neurons.
Developed the principle of conservation of energy and demonstrated that it applies
to mechanics, heat, light, electricity and magnetism.
Demonstrated that muscle metabolism conserves energy.
Invented the field of psychology with his student Wilhelm Wundt.
In 1863, Helmholtz published "On the Sensations of Tone", which became the standard
reference for the next century.
Students: Max Planck, Heinrich Kayser, Eugen Goldstein, Wilhelm Wien, Arthur
Konig, Henry Augustus Rowland, Albert A. Michelson, Wilhelm Wundt, Fernando
Sanford and Michael I. Pupin.
Amati (1505-1577) lived in Cremona, Italy, and developed the first violins, violas,
and cellos.
A gas molecule moving in 3 dimensions has 3 degrees of freedom and so the
mean kinetic energy is
The speed of sound is
Using the ideal gas law,
If we express the ideal gas law in terms of density,
We can change the sound speed by using a gas with a different value of M.
The fact that Newton's calculation differed from the measured speed is due to
the fact that air consists of diatomic molecules (nitrogen and oxygen). This
was the first solid clue for the existence of atoms, and it also contained a
clue for quantum mechanics.
In Newton's time it was not known that changing the volume of a gas changes its
temperature, which modifies the relationship between density and pressure.
This was discovered by Charles in 1802 (Charles' law).
For a diatomic gas there are also two rotational degrees of freedom. In this
case d=5.
In general,
The fact that Gamma=7/5 for air was a clue for the existence of both atoms,
molecules, and quantum mechanics.
For dark energy,
As a substance expands it does work on its surroundings according to its pressure.
Dark matter consists of pointlike particles but they rarely interact with other
particles and so they exert no pressure.
Wave type Wave speed squared
Sound in air 1.4 * Pressure / Density
String wave Tension / (Density * CrossSectionalArea)
Longitudinal wave BulkModulus / Densty
Shear wave ShearModulus / Density
Torsion wave ShearModulus / Density
Deep water wave GravityConstant * Wavelength / (2 Pi) (If Depth > .5 Wavelength)
hallow water wave GravityConstant * Depth (If Depth < .5 Wavelength)
GravityConstant = 9.8 meters/second^2
If the wave speed doesn't depend on the frequency then waves propagate without
changing shape (without dispersion). This applies to all waves except for deep
water waves.
Bulk Density Sound speed
modulus (g/cm^3) (km/s)
(GPa)
Air .00014 .0012 .34
Water 2.2 1.0 1.43
Wood 13 1 3.6
Granite 100 2.75 6.0
Steel 170 7.9 6.1
Diamond 443 3.5 12.0
Beryllium 130 1.85 12.9 Fastest sound speed of any material
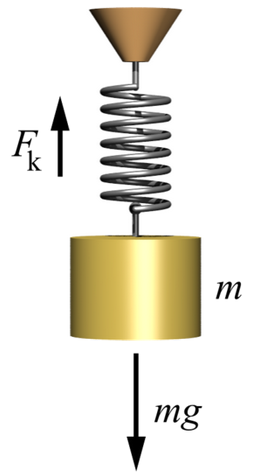
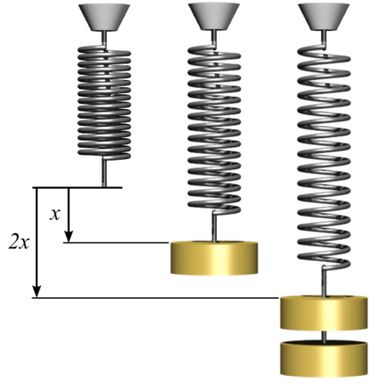
x = Displacement of the spring when a force is applied
K = Spring constant
Force = Force on the spring
= K x (Hooke's law)
Force = Tension force on the wire
X = Length of wire under zero tension force
x = Increase in length of the wire when a tension force is applied
Area = Cross-sectional area of the wire
Stress= Force / Area (Pressure, measured in Pascals or Newtons/meter^2)
Strain= Fractional change in length of the wire
= x/X
Young = Tensile modulus or "Young's modulus" for the (Pascals)
Hooke's law in terms of stress and strain is
Stress = Young * Strain
Young = K X / Area
If the Young's modulus of a string is too high it is too stiff to play.
This is why the core of a string is often made from an elastic material such
as nylon or gut.


Tensile yield strength = Maximum stress before the material irreversibly deforms
Tensile strength = Maximum stress before the material breaks




Density = Density of the wire
Stress = Force/Area on the wire
Strain = Fractional change in length of the wire
StressMax= Maximum stress before breaking
= Tensile strength
StrainMax= Tensile strain strength. Maximum strain before breaking
Young = Young's modulus
= Stress/Strain
Yield = Yield modulus
= Stress for which the material irreversibly deforms
Toughness= Energy/volume in the wire when at maximum stress
= .5 * StressMax^2 / Young
U = Toughness/Density
= Energy/kg in the wire when at maximum stress
Stress = Young * Strain
StressMax = Young * StrainMax
Toughness = .5 * Young * StrainMax^2
= .5 * StressMax^2 / Young
The ability of a material to keep an edge is related to its Young's modulus
and tensile strength.

Density = Density of the wire
Stress = Force/Area on the wire
Strain = Fractional change in length of the wire
StressMax= Maximum stress before breaking
= Tensile strength
StrainMax= Tensile strain strength. Maximum strain before breaking
Young = Young's modulus
= Stress/Strain
Yield = Yield modulus
= Stress for which the material irreversibly deforms
Toughness= Energy/volume in the wire when at maximum stress
= .5 * StressMax^2 / Young
U = Toughness/Density
= Energy/kg in the wire when at maximum stress
Stress = Young * Strain
StressMax = Young * StrainMax
Toughness = .5 * Young * StrainMax^2
= .5 * StressMax^2 / Young
The ability of a material to keep an edge is related to its Young's modulus
and tensile strength.

Young's Yield Tensile Tensile Tough Tough/ Brinell Density Poisson
modulus strengh strain density (GPa) (g/cm^3)
(GPa) (Gpa) (GPa) (MPa) (J/kg)
Beryllium 287 .345 .448 .0016 .350 189 .6 1.85 .032
Magnesium 45 .100 .232 .0052 .598 344 .26 1.74 .29
Aluminum 70 .020 .050 .00071 .018 15 .245 2.70 .35
Titanium 120 .225 .37 .0031 .570 54 .72 4.51 .32
Chromium 279 .282 .00101 .143 199 1.12 7.15 .21
Iron 211 .100 .35 .0017 .290 37 .49 7.87 .29
Cobalt 209 .485 .760 .0036 1.382 155 .7 8.90 .31
Nickel 170 .190 .195 .0011 .112 12.5 .7 8.91 .31
Copper 130 .117 .210 .0016 .170 19 .87 8.96 .34
Molybdenum 330 .324 .00098 .159 15 1.5 10.28 .31
Silver 83 .170 .0020 .174 17 .024 10.49 .37
Tin 47 .014 .200 .0043 .426 59 .005 7.26 .36
Tungsten 441 .947 1.51 .0037 2.585 134 2.57 19.25 .28
Rhenium 483 .290 1.07 .0024 1.298 62 1.32 21.02 .30
Osmium 590 1.00 .0018 .893 40 3.92 22.59 .25
Iridium 528 2.0 .0038 3.788 168 1.67 22.56 .26
Platinum 168 .165 .00098 .081 3.8 .32 21.45 .38
Gold 78 .127 .0016 .103 5.3 .24 19.30 .44
Lead 16 .012 .00075 .045 3.8 .44 11.34 .44
Al Alloy 70 .414 .483 .0069 1.666 595 2.8
Brass 125 .20 .55 .0044 1.210 139 8.73
Bronze 120 .800 .0067 2.667 300 8.9
Steel 250 .250 .55 .0022 .605 77 7.9 .30
Stainless 250 .52 .86 .0034 1.479 185 8.0 .30
W-C 650 .345 .00053 .092 5.9 15.63
Si-C 450 - 3.44 .0076 13.10 4100 3.21
Rubber .1 .016 .5
Nylon 3 .045 .075 .025 .938 815 1.15
Carbon fiber 181 1.600 .0088 7.07 4040 1.75
Kevlar 100 3.62 3.76
Zylon 180 2.70 5.80 1.56
Colossal tube - 7 .116 Carbon colossal nanotube
Nanorope ~1000 - 3.6 .0036 6.5 4980 1.3 Rope made from nanotubes
Nanotube 1000 - 63 .063 1980 1480000 1.34 Carbon nanotube
Graphene 1050 - 160 .152 12190 12190000 1.0
Carbyne 32100 Unstable
Air 0 0 0 0 0 0 .0012
Water 0 0 0 0 0 0 1.00
Ice .001 .33
Cork low 0
Glass 45 .033 2.53 .25
Concrete 30 .005 2.7 .2
Granite 70 .025 2.7 .2
Basalt .030
Marble 70 .015 2.6 .2
Skin .015 .020 2.2
Bone 14 .120 .130 .0093 604 377 1.6
Balsa
Pine .04
Oak 11
Bamboo .50 .4
Ironwood 21 .181 .0086 780 650 1.2
Tooth enamel 83
Human hair .380
Spider silk 1.0 1.3
Sapphire 345 .4 1.9 .0055 5232 1315 3.98 .28
Diamond 1220 1.6 2.8 .0023 3210 920 1200 3.5 .069
Young's Yield Tensile Tensile Tough Tough/ Brinell Density Poisson
modulus strengh strain density (GPa) (g/cm^3)
(GPa) (Gpa) (GPa) (kPa) (J/kg)
The listed strain is for when the material is at the breaking point.
Energy/mass
(MJ/kg)
Fission 69500000
Diesel fuel 47
Lithium battery .95
Supercapacitor .018
Spring .0003









F = Maximum force applied to the center of a beam before it breaks
X = Beam length
Y = Beam thickness
Z = Beam height
x = Deflection of the beam at the center when under force "F"
ShearStrength = 3 F X / (2 Y Z^2)
A = Area of the column
B = Bulk strength of the column
F = Force required to squash a column
= B A
A column's resistance to buckling is determined by the Young's modulus.
Suppose a column is a hollow cylinder.
L = Length of the column
R = Outer radius of the column
r = Inner radius of the column (r=0 if the cylinder is not hollow)
Y = Young's modulus
Q = Dimensionless effective length of the column
= .5 if both ends are fixed
= 2 if one end is fixed and the other end is free to move laterally
= 1 if both ends are pinned (hinged and free to rotate)
= .699 if one end is fixed and the other is pinned
F = Force required to buckle the column
F = .5 Pi Y (R-r) / (Q L)
If a column's buckling limit is equal to its squashing limit then (assume r=0)
R/L = (Q/Pi) * (2B/Y)
Z = Height of a beam
X = Length of a beam
Y = Width of a beam
Area = Surface area of the top face of the beam
= X Y
Force = Transverse force on the top face of the beam in the X direction
x = Transverse displacement of the top face of the beam when a transvere
force is applied
ShearStress = Force / (X Y)
Shearstrain = x/Y
ShearModulus = ShearStress / ShearStrain
ShearYield = Shear stress for which the material deforms irreversibly
ShearStrength = Maximum shear stress before breaking
ShearStrainMax= Maximum strain before breaking
ShearToughness= Energy/Volume absorbed by the material when at maximum strain
= .5 ShearModulus * ShearStrainMaax^2
= .5 ShearStrength^2 / ShearModulus
ShearStress = ShearModulus * ShearStrain
ShearStrength = ShearModulus * ShearStrainMax
Tensile strain and shear strain have analogous elastic variables.
TensileStress <--> ShearStress
Tensilestrain <--> Shearstrain
Tensilemodulus <--> ShearModulus
TensileYield <--> ShearYield
TensileStrength <--> ShearStrength
TensileStrainMax <--> ShearStrainMax
TensileToughness <--> ShearToughness
The bulk modulus is analogous to the tensile modulus and the strain modulus.








dX = Fractional increase in length of the wire
dY = Fractional decrease in diameter of the wire
PoissonRatio = dY / dX



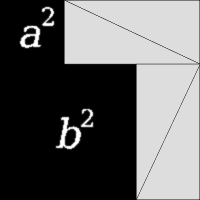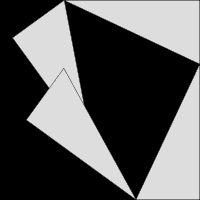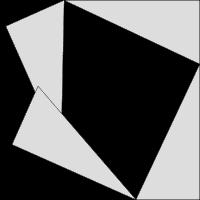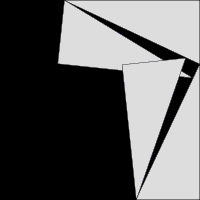
2 * (1 + PoissonRatio) * ShearModulus = TensileModulus
3 * (1 - 2*PoissonRatio) * BulkModulus = TensileModulus
The Poisson ratio for most metals is in the range of 1/3 and for rubber it is 1/2.
If we assume the Poisson ratio is 1/3 then
(8/3) * ShearModulus = TensileModulus
Materials based on carbon chains differ from isotropic materials
in that they tend to have a large tensile strength and a low shear strength.
These materials are good for wires.
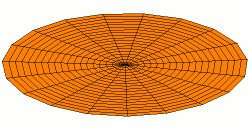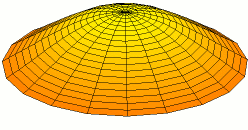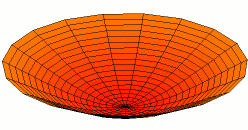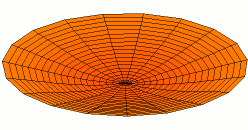
Vertical axis = ShearModulus
Horizontal axis = TensileModulus / (2 + 2*PoissonRatio)








.png)
Brinell = A measure of a material's resistance to dents, measured in Pascals
Mohs = A dimensionless measure of a material's resistance to dents
The Mohs scale of mineral hardness reflect's a material's ability to resist scratching.
If two materials are scraped together then the material with the lower Mohs value will
be scratched more. Diamond has the largest Mohs value of any material.
Mohs
Diamond 10
RhB2 9.5
Silicon carbide 9.5
Corundum 9
Tungsten carbide 9
Chromium 8.5
Emerald 8
Topaz 8
Tungsten 8
Hardened steel 8
Quartz 7
Osmium 7
Rhenium 7
Vanadium 7
If a material has a large Brinell hardness then it has a large Mohs hardness.
The reverse is not necessarily true. Materials exist with a large Mohs hardness
and a small Brinell hardness.

The Brinell hardness is related to the tensile modulus and tensile strength.


Vickers Tensile Tensile Tensile Tensile Poisson
hardness modulus strength tough strain
(GPa) (GPa) (GPa) (kPa) (GPa)
Hardened steel .8 250 .55 .29
Osmium 590 1.00 893 .25
Cobalt 1.04 209 .76 .31
Chromium 1.06 279 .282 143 .00101 .21
Tantalum 1.2 186 .90 .34
Beryllium 1.67 287 .448 .032
Iridium 2.2 528 2.0 3788 .0038 .26
Sapphire 2.3 345 1.9 5232 .0055 .28
Uranium 2.5 208 .625 .23
Si-C 2.6 450 3.44 13100 .0076 .19
W-C 2.6 650 .345 92 .00053 .23
Molybdenum 2.74 330 .324 159 .00098 .31
Ti-N 3.0 .25
Ti-C 3.2 439 .119 .19
Titanium 3.42 120 .37 570 .0031 .32
Tungsten 4.6 441 1.51 2585 .0037 .28
Boron 4.9 400 3.1
BN 6.0 100 .083 .27
Rhenium 7.58 483 1.07 1298 .0024 .30
Rhodium 8.0 275 .951 .26
Diamond 10.0 1220 2.8 3210 .0023 .069
All hard materials have a small Poisson ratio.

Density Price
(g/cm^3) ($/g)
Water 1.0
Nylon 1.2
Gut 1.5
Synthetic 2.5
Aluminum 2.8 <.01
Titanium 4.5 .01
Steel 7.9 <.01
Nickel 8.9 .01
Silver 10.5 .6
Tungsten 19.2 .05
Gold 19.3 24
Rhenium 21.0 6
Platinum 21.4 88
Iridium 22.56 13
Osmium 22.59 12 Densest element
Tungsten is the only dense metal that is not expensive.

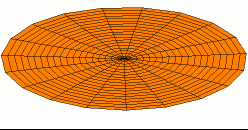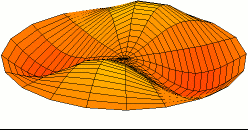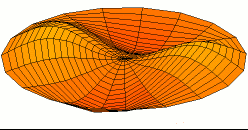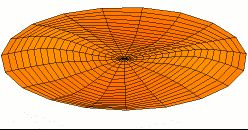
Color = Shear Modulus. Red is low, orange is medium, and white is high.
Dot size = Density
Shear data
Density data
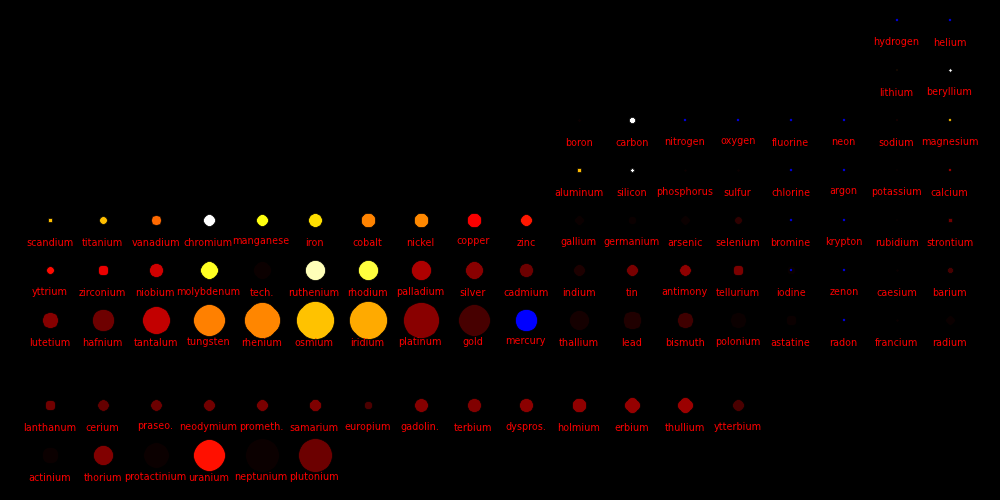
Color = Shear Modulus / Density A measure of a material's "strength to weight" ratio
Dot size = Density
The metals with the highest strength to weight ratio are Chromium, Ruthenium, and
Beryllium.

Dot size = (Shear Modulus)^(1/3) An indicator of a material's strength
Dot color = Melting point
White = Highest melting points
Red = Lowest melting points
Blue = Elements that are a gas or a liquid at room temperature and pressure.
Liquids and gases have a shear modulus of 0.
Rocket cones are made from materials with a high melting point, a high shear
strength, and a high atomic mass. Tungsten is the element of choice,
especially because it's vastly cheaper than Rhenium, Osmium, and Iridium.

Color = Price per kilogram Red is low, orange is medium, white is high
Blue indicates the element is radioactive with a
short half life
Dot size = -log(SolarAbundance) The smaller the dot, the more abundant the element
Price data

Dot size = Atomic radius
= (AtomicMass / Density)**(1/3)
For gases, the density at boiling point is used.

Dot size = [Shear modulus / Density]**(1/2)
Color = Poisson ratio, ranging from red to white

Dot size = [Brinell hardness / Density]**(1/2)
Color = Poisson ratio, ranging from red to white
Brinell hardness is difficult to define for diamond, although it is substantially
larger than that for any other element. A nominal value is used in the table only
to indicate that it is large.
Earliest Shear Melt Density
known use Strength (K) (g/cm^3)
(year) (GPa)
Wood < -10000 15 - .9
Rock < -10000
Carbon < -10000
Diamond < -10000 534 3800 3.5
Gold < -10000 27 1337 19.3
Silver < -10000 30 1235 10.5
Sulfur < -10000
Copper -9000 48 1358 9.0
Lead -6400 6 601 11.3
Brass -5000 ~40 Copper + Zinc
Bronze -3500 ~40 Copper + Tin
Tin -3000 18 505 7.3
Antimony -3000 20 904 6.7
Mercury -2000 0 234 13.5
Iron -1200 82 1811 7.9
Arsenic 1649 8 1090 5.7
Cobalt 1735 75 1768 8.9 First metal discovered since iron
Platinum 1735 61 2041 21.4
Zinc 1746 43 693 7.2
Tungsten 1783 161 3695 19.2
Chromium 1798 115 2180 7.2
Stone age antiquity
Copper age -9000
Bronze age -3500
Iron age -1200
Bronze holds an edge better than copper and it is more corrosion resistant.
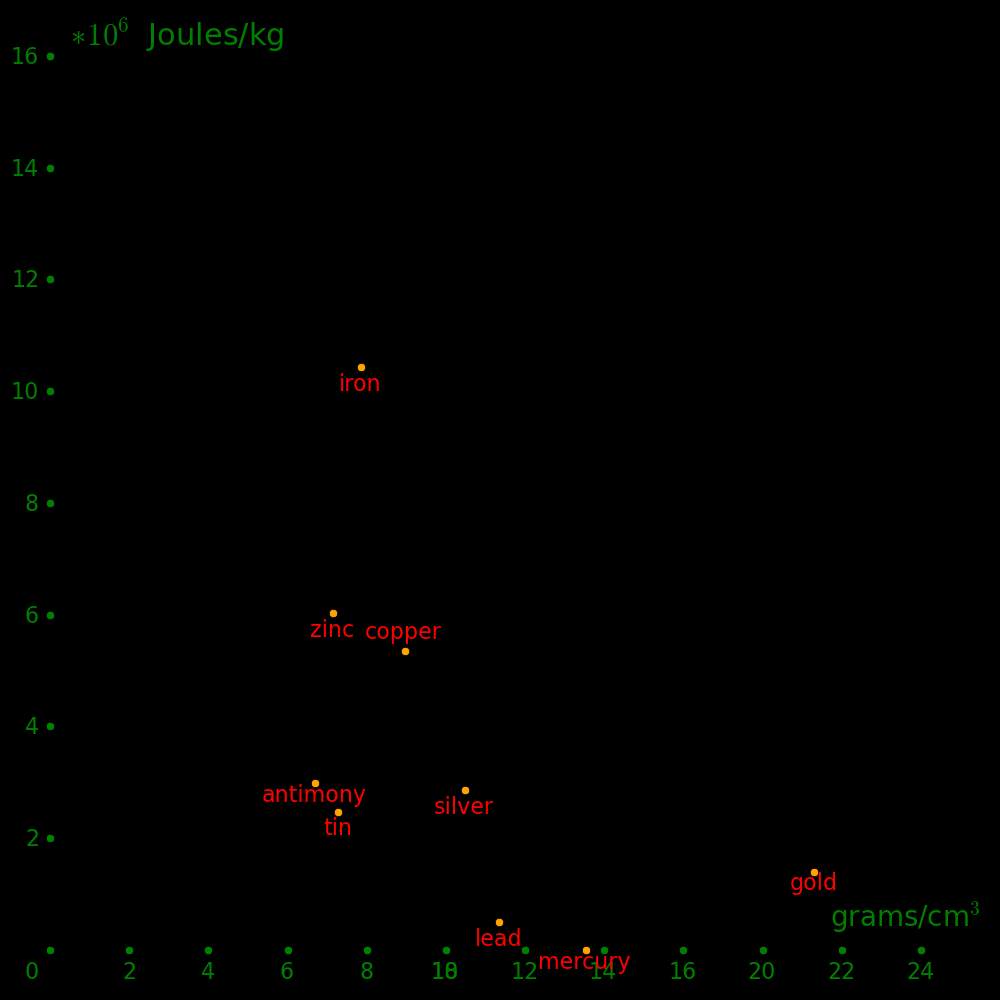
Horizontal axis: Density
Vertical axis: Shear modulus / Density (Strength-to-weight ratio)
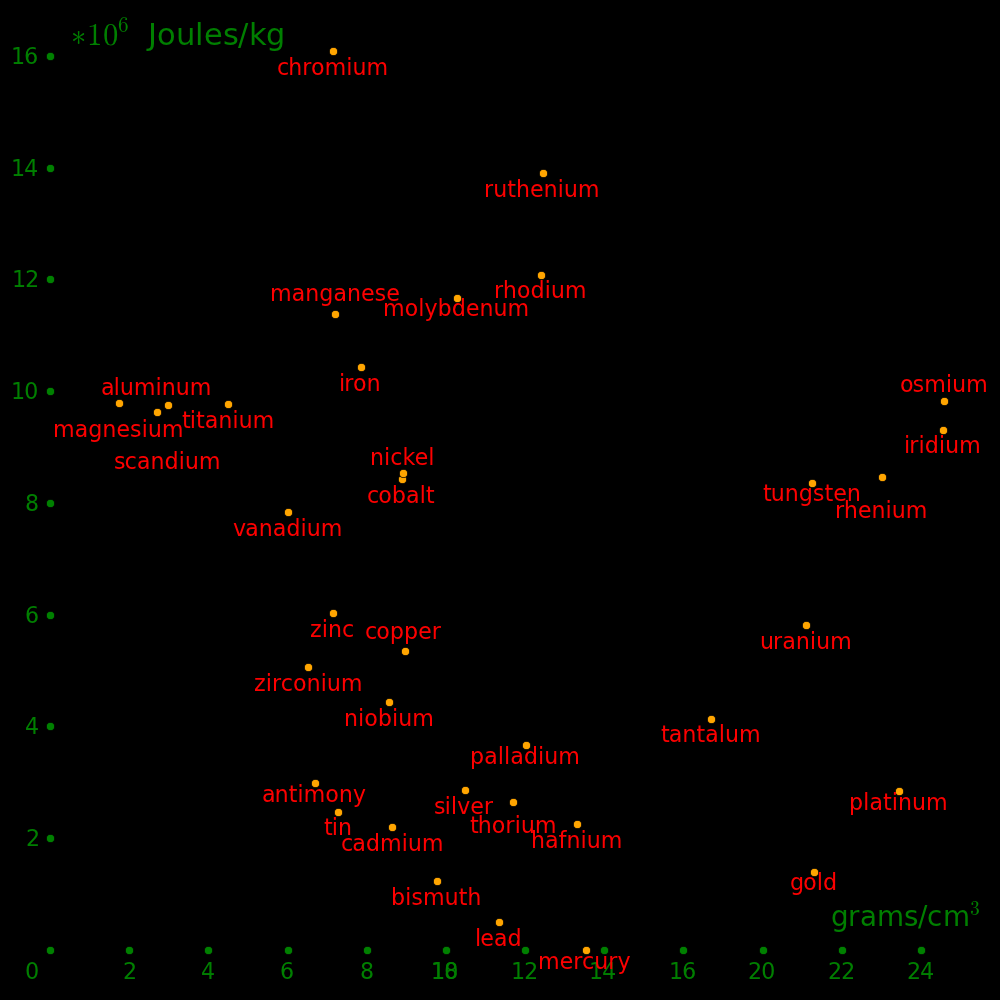
Horizontal axis: Density
Vertical axis: Shear modulus / Density (Strength-to-weight ratio)
Beryllium is beyond the top of the plot.













.jpg)


























Metal impurity Color
Chromium Red
Iron Blue
Titanium Yellow
Copper Orange
Magnesium Green








.gif)













Year Young Tensile Strain Density Common
(GPa) strength (g/cm^3) name
(GPa)
Gut .2
Cotton Ancient .1 1.5
Hemp Ancient 10 .3 .023
Polyamide 1939 5 1.0 .2 1.14 Nylon, Perlon
Polyester 1941 15 1.0 .067 1.38
Polypropylene 1957 .91
Polyethylene 1939 117 1.4 Dacron
Carbon fiber 1968 3.0 1.75
Aramid 1973 135 3.0 .022 1.43 Kevlar
HMPE 1975 100 2.4 .024 .97 Dyneema, Spectra
LCAP 1990 65 3.8 .058 1.4 Vectran
Vectran HT 75 3.2 .043 1.41 Vectran
Vectran NT 52 1.1 .021 1.41 Vectran
Vectran UM 103 3.0 .029 1.41 Vectan
PBO 1985 280 5.8 .021 1.52 Zylon
Nanorope ~1000 3.6 .0036 1.3
Nanotube 1000 63 .063 1.34
Graphene 1050 160 .152 1.0
Strain = Strength / Young
Carbon fiber is not useful as a rope.




Small value Large value
Tensile modulus Climbing rope Bicycle spokes
Tensile yield
Tensile strength Violin strings
Tensile max strain Climbing rope
Tensile toughness Elevator cable
Shear modulus Golf driver Bike frame
Shear yield Spring
Shear strength Beam
Shear toughness Sword interior
Shear max strain Golf driver
Bulk modulus Pillow
Brinell hardness Machining metal Sword edge
Mohr hardness Pencil lead Cutting tools
Poisson ratio
Density Airplane frame Bullet
Some examples of materials used for high-performance applications are
Rocket cones Tungsten
Wire Zylon, Sapphire, Carbon nanorope
Sword inerior Aluminum alloy, Sapphire
Sword edge Diamond
Clock escapement Diamond, Tungsten carbide
Formula-1 brakes Carbon
Bullet Lead, Tungsten, Uranium, Osmium
Lubricants Fullerines
Brass is a useful machining metal because it is easy to cut.
Example
Tensile strength Maximum stress on a wire
Shear modulus Stiffness of a beam or column
Shear strength Maximum stress on a beam or column
Brinell hardness Sword edge
Mohr hardness Cutting tools
Density Bullets
Below is a table of the stoutest engineering materials.
Young's Yield Tensile Tensile Tough Tough/ Brinell Density Poisson
modulus strengh strain density (GPa) (g/cm^3)
(GPa) (Gpa) (GPa) (MPa) (J/kg)
Beryllium 287 .345 .448 .0016 .350 189 .6 1.85 .032
Mg alloy 45 .100 .232 .0052 .598 344 .26 1.74 .29
Al alloy 70 .414 .483 .0069 1.666 595 .245 2.8 .35
Titanium 120 .225 .37 .0031 .570 54 .72 4.51 .32
Chromium 279 .282 .00101 .143 199 1.12 7.15 .21
Iron 211 .100 .35 .0017 .290 37 .49 7.87 .29
Cobalt 209 .485 .760 .0036 1.382 155 .7 8.90 .31
Nickel 170 .190 .195 .0011 .112 12.5 .7 8.91 .31
Copper 130 .117 .210 .0016 .170 19 .87 8.96 .34
Molybdenum 330 .324 .00098 .159 15 1.5 10.28 .31
Tin 47 .014 .200 .0043 .426 59 .005 7.26 .36
Tungsten 441 .947 1.51 .0037 2.585 134 2.57 19.25 .28
Rhenium 483 .290 1.07 .0024 1.298 62 1.32 21.02 .30
Osmium 590 1.00 .0018 .893 40 3.92 22.59 .25
Iridium 528 2.0 .0038 3.788 168 1.67 22.56 .26
Brass 125 .20 .55 .0044 1.210 139 8.73
Bronze 120 .800 .0067 2.667 300 8.9
Steel 250 .250 .55 .0022 .605 77 7.9 .30
Stainless 250 .52 .86 .0034 1.479 185 8.0 .30
W-C 650 .345 .00053 .092 5.9 15.63
Si-C 450 - 3.44 .0076 13.100 4100 3.21
Carbon fiber 181 1.600 .0088 7.070 4040 1.75
Kevlar 3.62 3.76
Zylon 180 2.70 5.80 1.56
Nanorope ~1000 - 3.6 .0036 6.5 4980 1.3 Rope made from nanotubes
Nanotube 1000 - 63 .063 1980 1480000 1.34 Carbon nanotube
Graphene 1050 - 160 .152 12190 12190000 1.0
ColossalTube low - 7 .116
Balsa
Bamboo .500 .4
Ironwood 21 .181 .0086 .780 650 1.2
Sapphire 345 .4 1.9 .0055 5.232 1315 3.98 .28
Diamond 1220 1.6 2.8 .0023 3.210 920 1200 3.5 .069
Young's Yield Tensile Tensile Tough Tough/ Brinell Density Poisson
modulus strengh strain density (GPa) (g/cm^3)
(GPa) (Gpa) (GPa) (kPa) (J/kg)
Element Density Melt Boil Young Young/ $/kg ppm in metallic
(g/cm^3) (K) (K) GPa Density asteroid
Tungsten 19.25 3693 5828 411 21.4 50 ~ 1
Rhenium 21.0 3459 5869 463 22.0 4600 ~ 1
Osmium 22.59 3306 5285 550 24.3 12000 2
Tantalum 16.7 3290 5731 186 11.1 400 ~ .5
Molybdenum 10.28 2896 4912 329 31.0 21 ~10
Niobium 8.75 2750 5017 105 12.0 40 ~ 3
Iridium 22.4 2739 4701 528 23.6 14000 2
Ruthenium 12.45 2607 4423 447 35.9 5500 5
Composition Teslas kJoules/ kAmps/ Max Density Tensile
meter^3 meter Temperature (g/cm^3) strength
(C) (GPa)
Neodymium Nd2Fe14B 1.4 440 2000 400 7.4 .075
Samarium-Cobalt SmCo5 1.15 240 1300 800 8.3 .035
Alnico 1.4 88 275 860
The composition of alnico alloys is typically 8-12% Al, 15-26% Ni, 5-24% Co, up to
6% Cu, up to 1% Ti, and the balance is Fe.








String Height of Height of
length Tension (Newtons) top string bottom string
(mm) E A D G C (mm) (mm)
Violin 320 80 50 45 45 3.2 5.2
Viola 388 65 55 55 55 4.8 6.2
Cello 690 160 130 130 130 5.2 8.2
Bass 1060 160 160 160 160
Guitar 650 120 120 120 120
Bass guitar 860 160 160 160 160
The height of the string is the distance from the fingerboard.
Values for a violin A-string
L = Length of a string = .32 meters
F = Vibration frequency of the string = 440 Hertz
V = Speed of a wave on the string = 281.6 meters/second
= 2 F L
For a given instrument and string frequency, the wavespeed is fixed.
WaveSpeed^2 = Tension / (Density * Pi * Radius^2)
The variables you can vary for a string are {Tension, Density, Radius}.
Once you have chosen the frequency and length of the string then these variables
are related by
Tension = Constant * Density * Radius^2
SoundSpeed^2 = (7/5) Pressure / Density
Force = Force on the string
A = Area of the string
S = Stress on the string
= Force / A
Smax = Tensile strength
= Maximum string stress before breaking
Z = Strength to weight ratio
Z = Smax / Density
Tensile Density Z/10^6 Young's
strength modulus
(GPa) (g/cm^3) (J/kg) (GPa)
Carbon nanotube 7 .116 60.3 Technology not yet developed
Nylon .045 1.15 .04 5
Kevlar 3.6 1.44 2.5
Zylon 5.8 1.5 3.9
Gut .2 1.5 .13 6
Magnesium alloy .4 1.8 .22
Aluminum .05 2.7
Titanium alloy .94 4.5 .21
Nickel .20 8.9
Chromium .28 7.2
Steel alloy 2.0 7.9 .25 220
Brass .55 8.7
Silver .17 10.5
Tungsten .55 19.2 .029
Gold .13 19.3
Osmium 1.0 22.6
Iridium
F = String frequency
R = String radius
A = String cross-sectional area
= Pi R^2
D = String density
L = String length
Force= String tension force (Newtons)
S = Tensile stress (Pascals)
= Force / A
Smax = Maximum string tensile stress before breaking
= Tensile strength
V = Speed of a wave on the string
= SquareRoot(P/D)
Z = String strength-to-weight ratio
= S/D
Fmax = Maximum frequency of a string
The maximum frequency of a string happens when S=Smax.
Fmax = V / (2L)
= SquareRoot(Smax/D) / (2L)
= SquareRoot(Z) / (2L)
The maximum frequency of a string depends on the strength-to-weight ratio Z.
Values for Z for various string materials are given in the table above.
Steel alloy is often used for the highest-frequency strings on a violin or
piano.
Gut Steel Zylon Carbon Tungsten
nanotube
Violin 563 781 2960 12100 266
Viola 465 644 2440 3160 220
Cello 261 362 1370 5620 123
Bass 170 236 895 3660 80
Guitar 277 385 1519 5973 131
Bass guitar 209 291 1148 4514 99
Frequencies are in Hertz.
Frequency = Constant * SquareRoot(Smax/D) / R
String frequency is inversely proportional to radius. A string can be made an
octave lower by doubling the radius.
-
Freq Length Diameter
(Hz) (mm) (mm)
Violin G 196 320 .46
Viola C 130 388 .62
Cello C 65 690 1.07
Bass E 41 1060 1.18
Guitar E 82 650 .90
Bass guitar E 41 860 1.7


Density Price
(g/cm^3) ($/g)
Zylon 1.5 Cheap
Tungsten 19.2 .05
Gold 19.3 40
Rhenium 21.0 10
Platinum 21.4 80
Iridium 22.4 20
Osmium 22.6 20
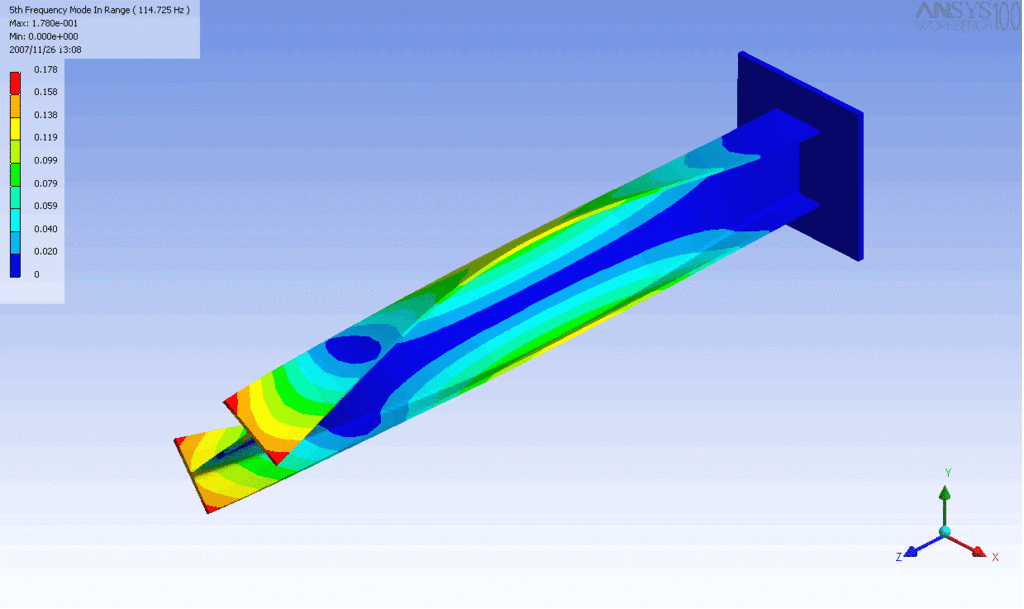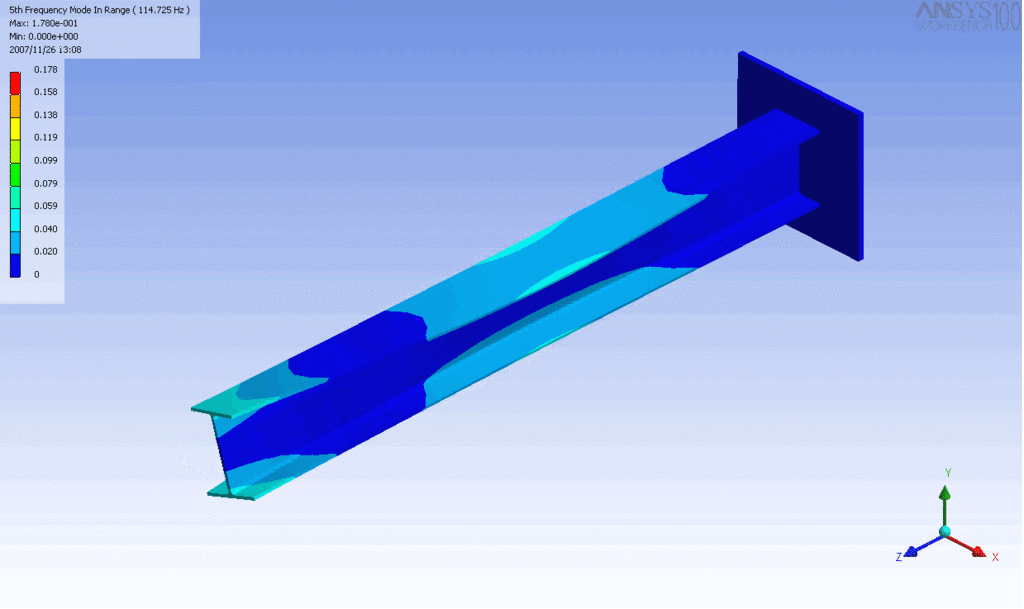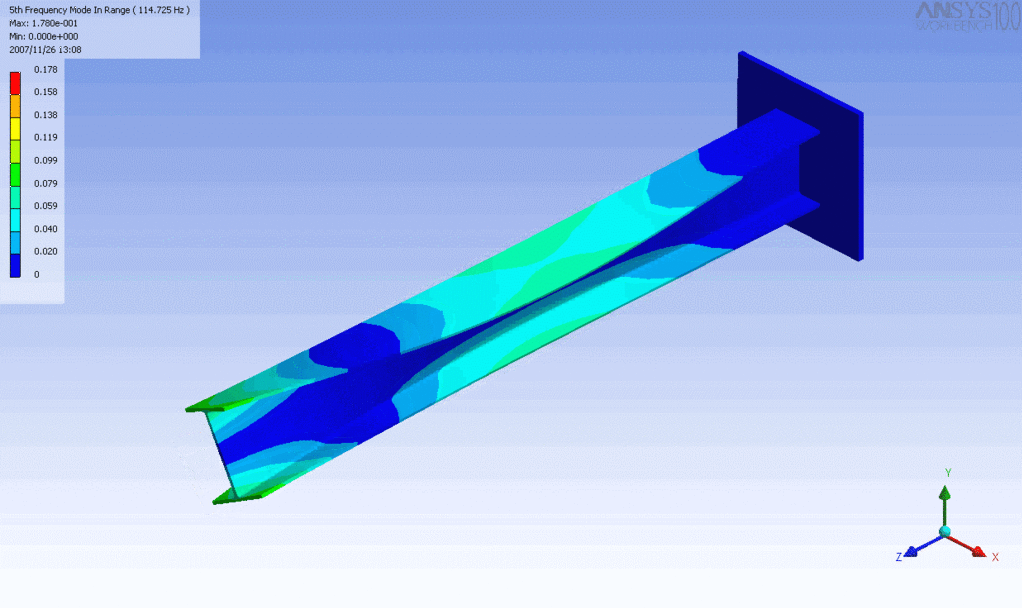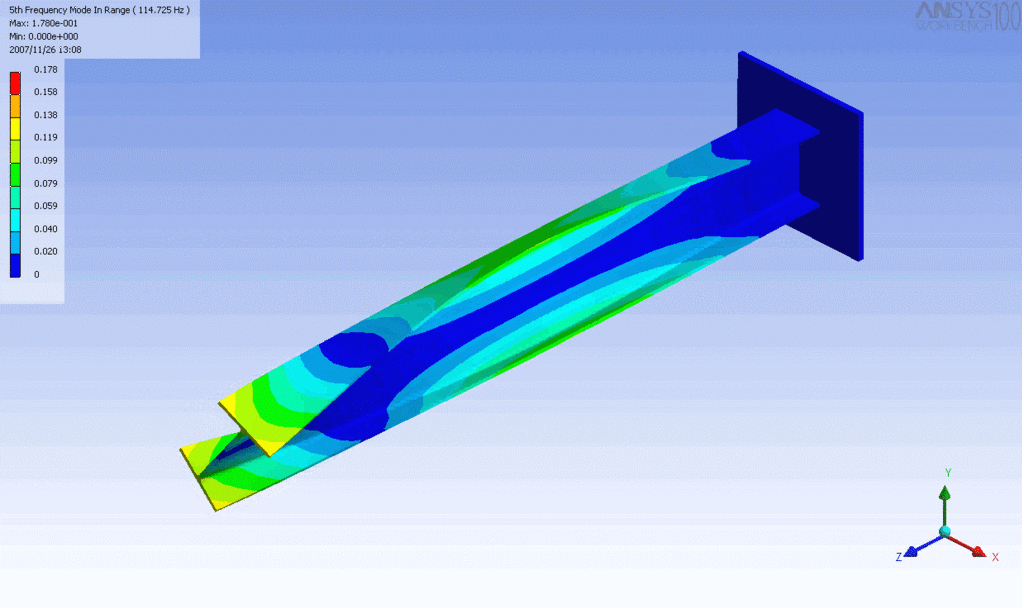

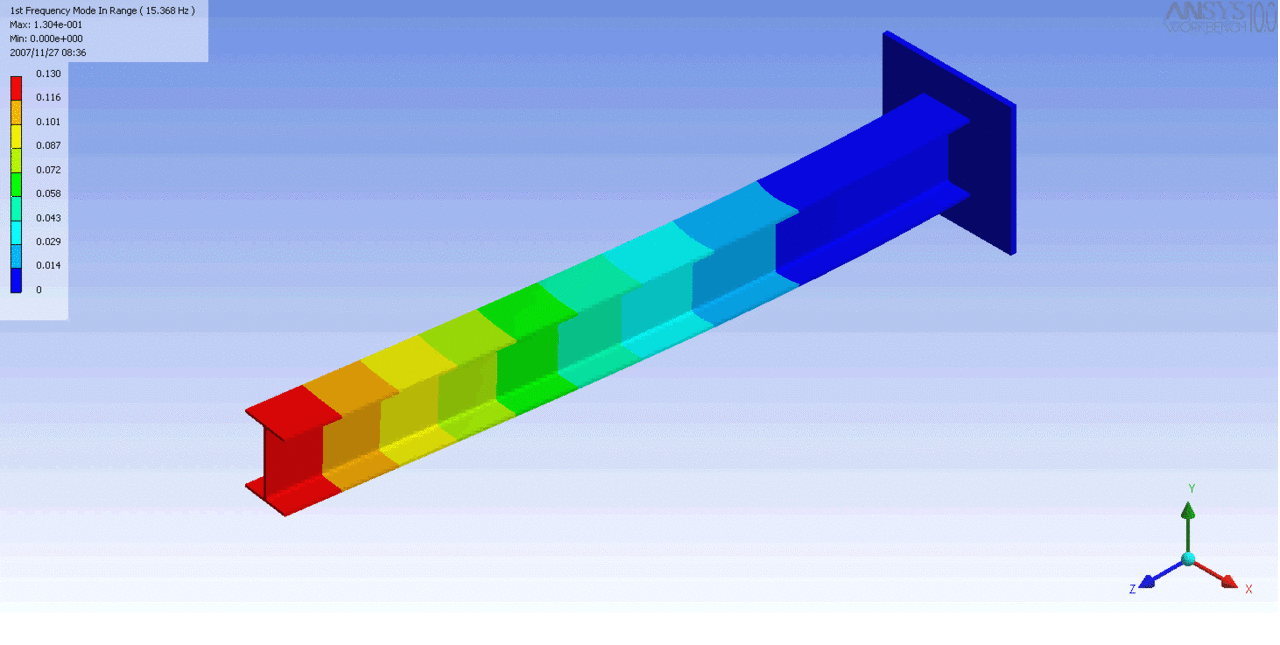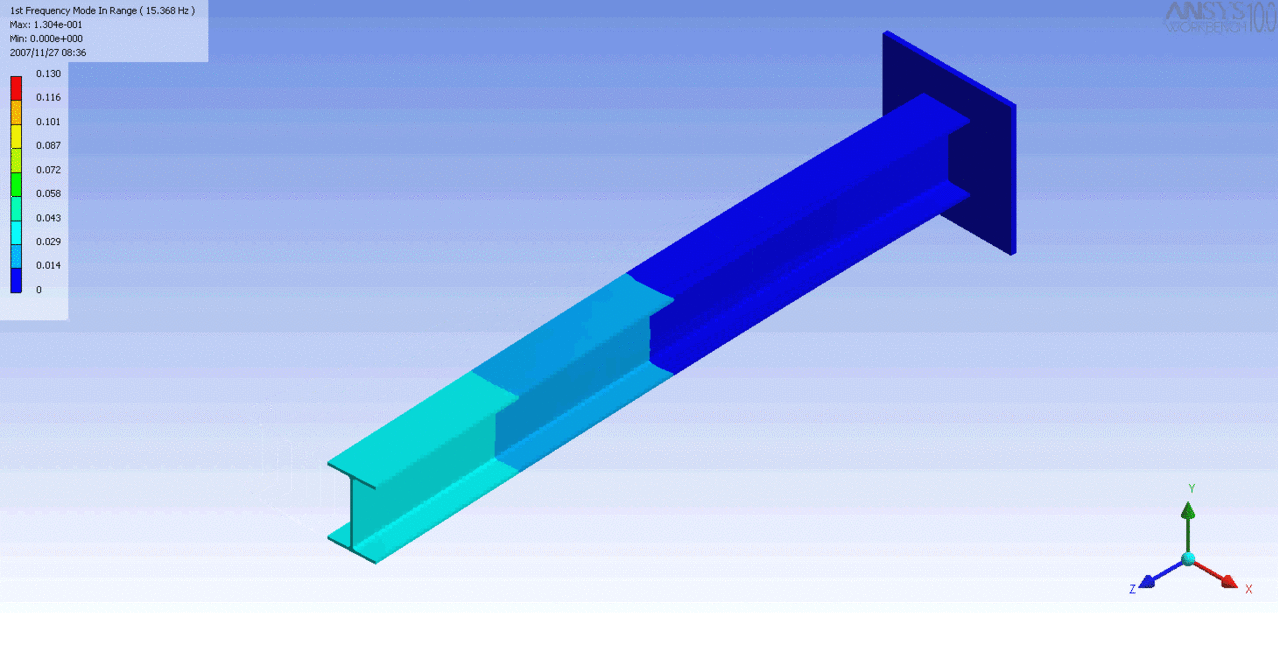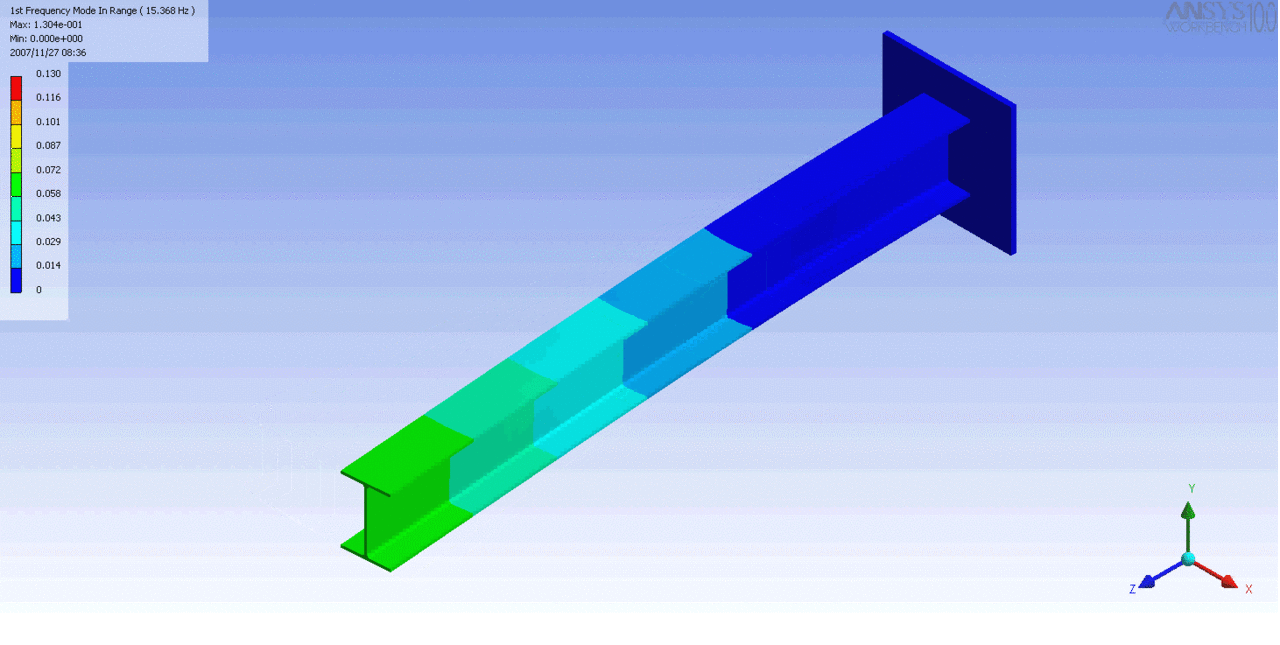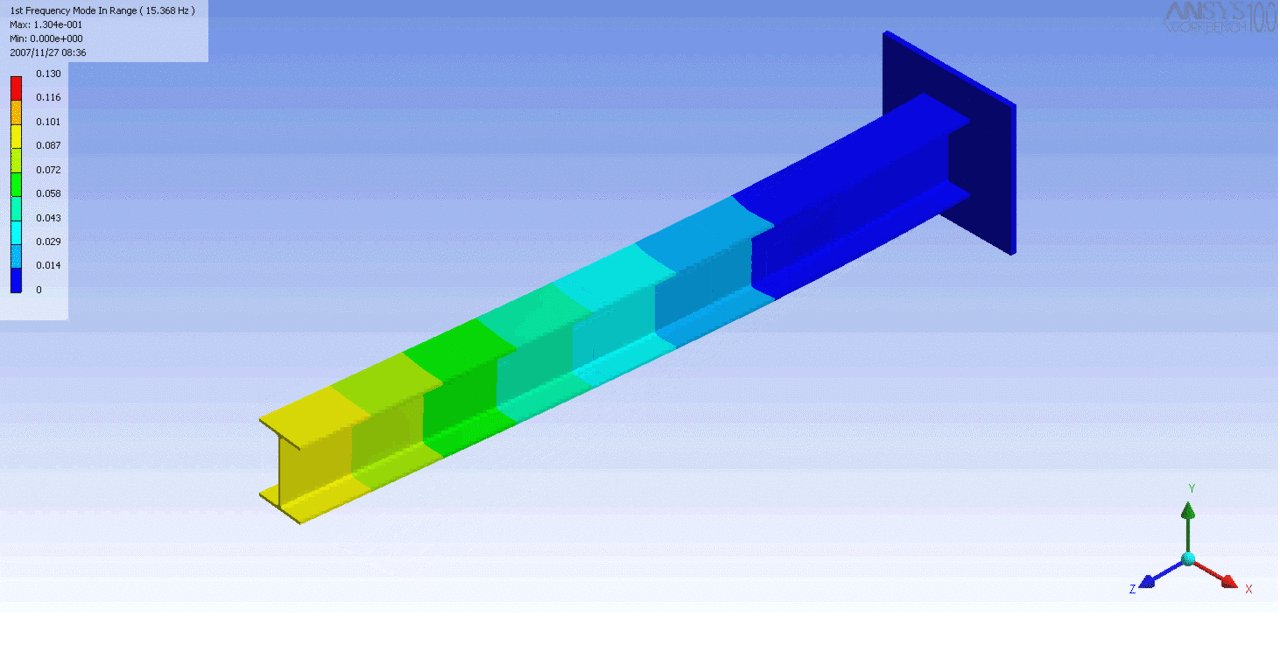

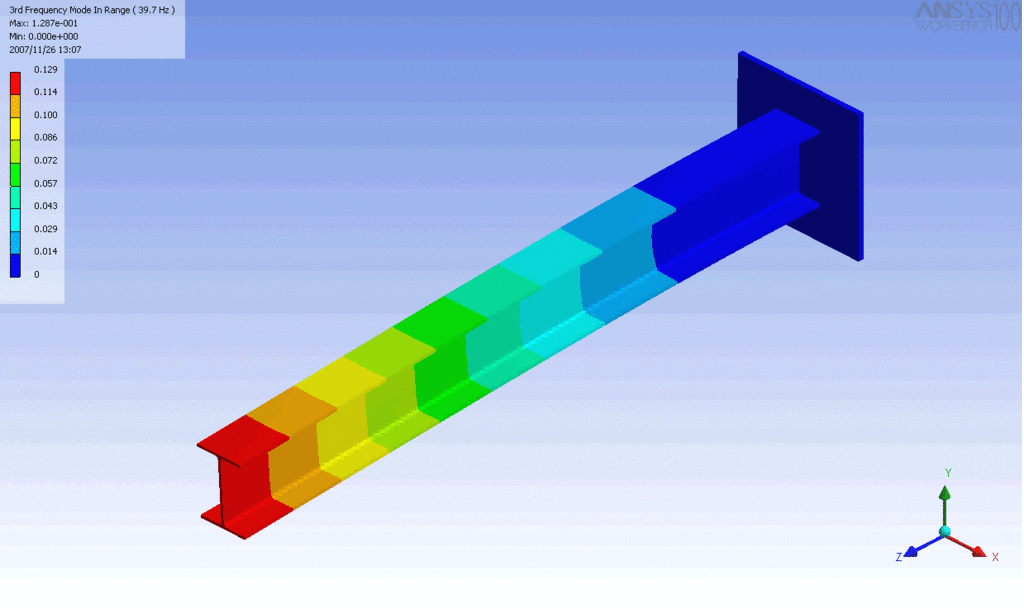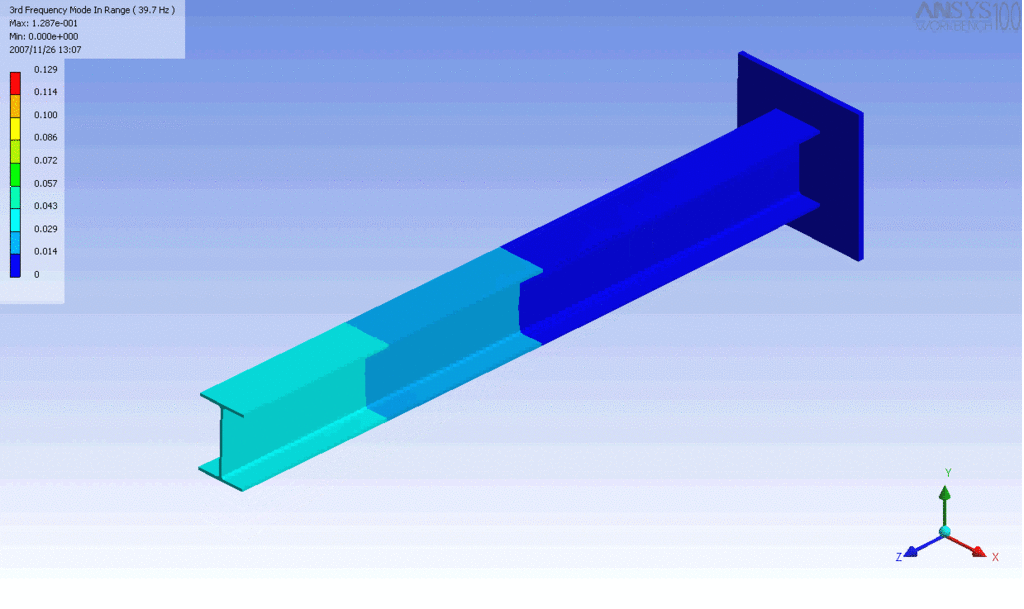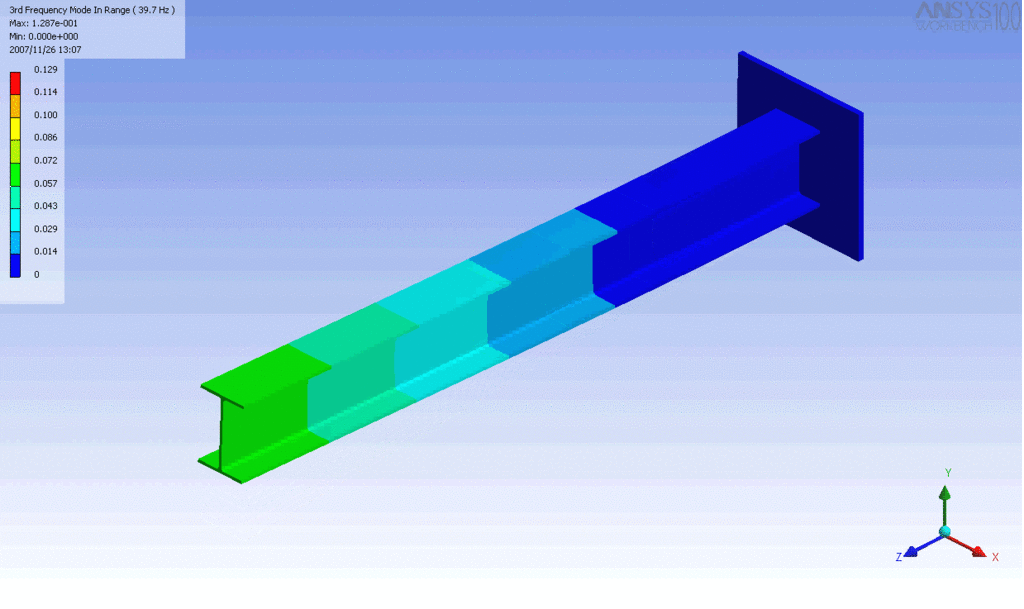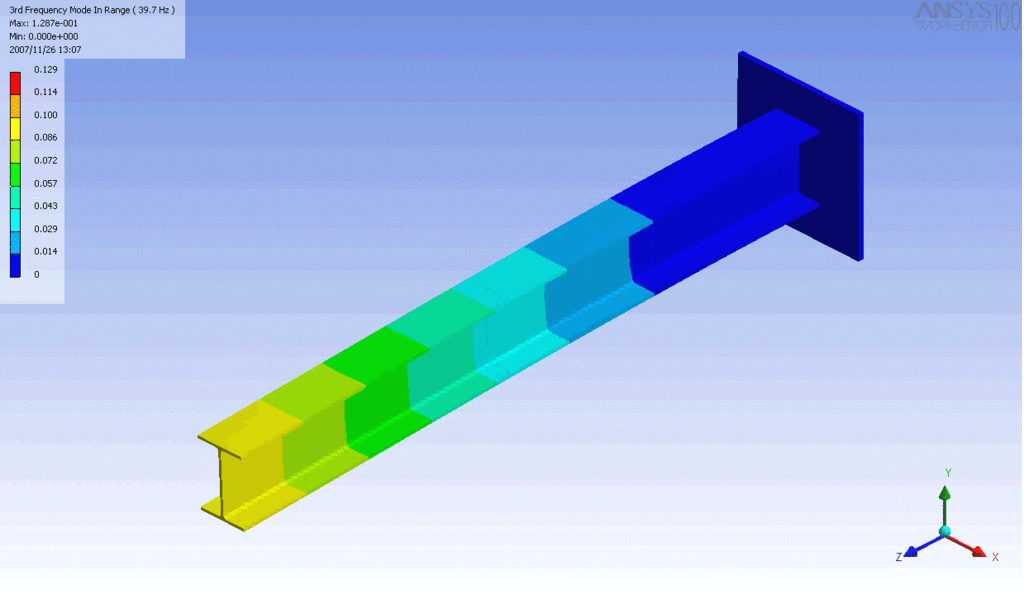
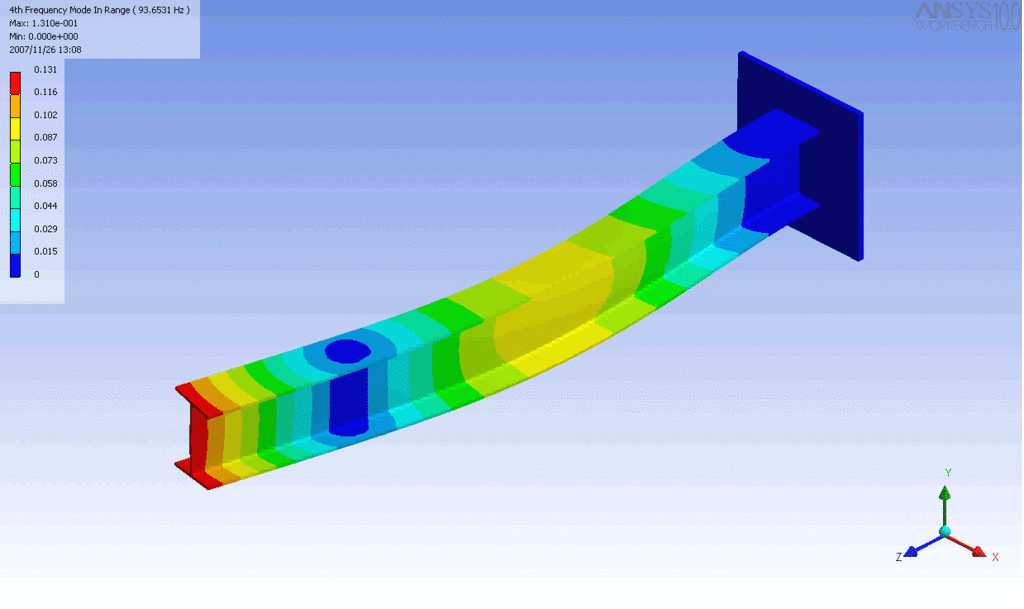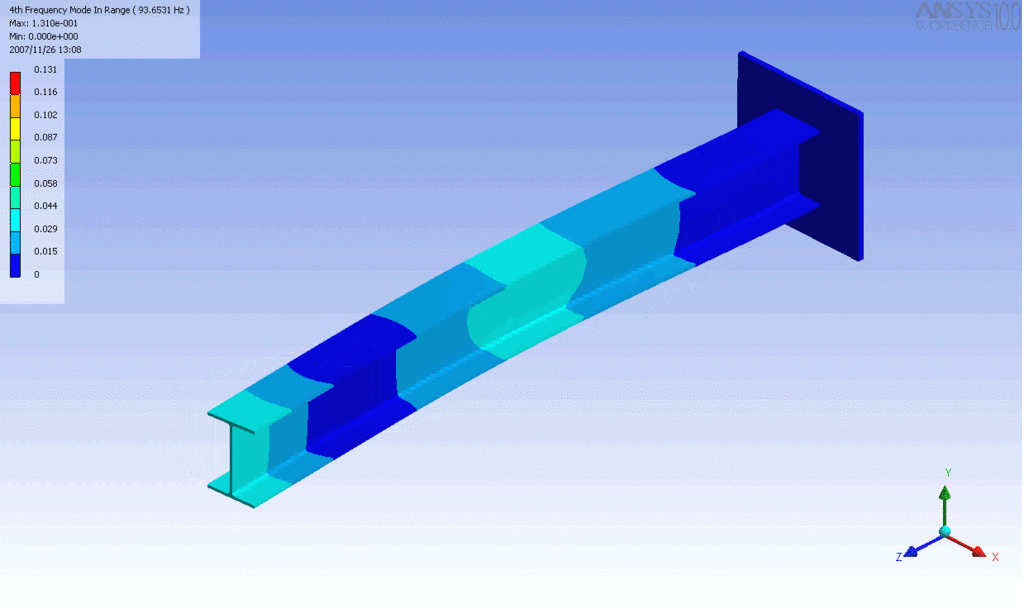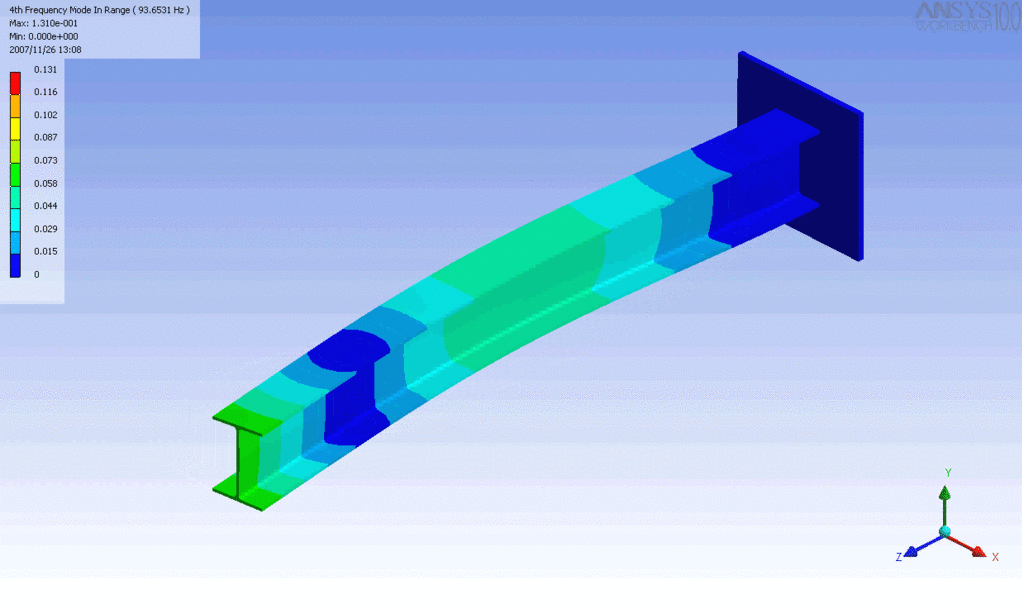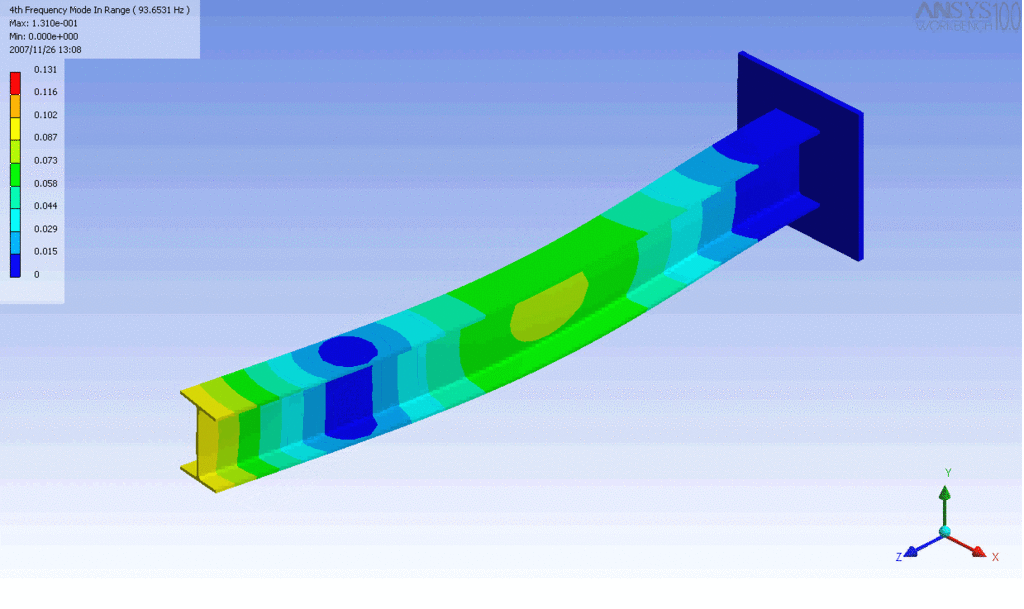
R = String radius
L = String length
D = String density
Y = Young's modulus for the string
Force= Tension force on the string
N = An integer greater than or equal to 1
Fn = Frequency of overtone N
= N F (1 + C N^2)
C = Constant of inharmonicity
= Pi^3 R^4 Y / (8 L^2 Force)
If C=0 then there is no inharmonicity and the overtones are exact integer multiples
of the fundamental mode. If the string has finite thickness then the frequencies
of the overtones shift.
C = Pi Force Y / (128 D^2 F^4 L^6)
Increasing the density decreases the inharmonicity.
String Tension Frequency Density Radius Young's C
length (Newtons) (Hertz) (g/cm^3) (mm) modulus
(mm) (GPa)
Violin E gut 320 80 660 1.5 .31 6 .000026
Violin E steel 320 80 660 7.9 .13 220 .000033
Violin G steel 320 45 196 7.9 .34 220 .00012
Viola C steel 388 55 130 7.9 .47 220 .00019
Cello C steel 690 130 65 7.9 .81 220 .000098
Bass E steel 1060 160 41 7.9 .92 220 .000047
Guitar E steel 650 140 82 7.9 .70 220 .000058
Bass guitar E 860 220 41 7.9 1.34 220 .00017
If we set the frequency shift from inharmonicity equal to the frequency resolution
for human hearing,
N^2 C = 1/170
If C=.0001 then N=7.7 (The inharmonicity appears at the 8th overtone)
L = Length of the string
R = Outer radius of the string
r = Radius of the inner core
= K R where K is a dimensionless constant
Y = Young's modulus of the core material
D = Density of the outer winding
Force= Force on the string
= k L where k is a constant
Y = Young's modulus of the core
S = Stress on the inner core
= Force / (Pi r^2)
s = Strain on the inner core
= S/Y
C = Constant of inharmonicity
= Pi^3 R^4 Y / (8 L^2 Force)
= Pi Force Y / (128 D^2 F^4 L^6)
The strain should be as large as possible to minimize the Young's modulus, but
if it is too large then the string loses functionality. We assume that the
strain is a constant value.
Force / (Pi r^2) = Y s
The larger the value of "r" the lower the value of "Y" and the lower the inharmonicity.
Force = Pi R^2 4 D F^2 L^2
= Pi r^2 Y s
We have
4 D F^2 L^2 = K^2 Y s
The inharmonicity is
C = Pi Force Y / (128 D^2 F^4 L^6)
= Pi Force 4 D F^2 L^2 / (128 K^2 s D^2 F^4 L^6)
= Pi Force / (32 K^2 D F^2 s L^4)
= Constant * Force / (F^2 L^4)
If we assume that
Force = Constant * L
then
C = Constant / (F^2 L^3)
The lowest practical frequency of an instrument scales as L^(-3/2).
Relative inharmonicity = 1/(Freq^2 Length^3)
The relative inharmonicity of the lowest string for various instruments is
given by the following table. The value is similar for all instruments.
Freq Length Relative inharmonicity
(Hz) (mm) = 1/(Freq^2 Length^3)
Violin G 196 320 .00079
Viola C 130 388 .00101
Cello C 65 690 .00072
Bass E 41 1060 .00050
Guitar E 82 650 .00054
Bass guitar E 41 860 .00094
Note Freq Tension Core Core Outer Core Core
(Hertz) stress radius radius Young strain
(N) (GPa) (mm) (GPa)
Viola C 130.4 50 .2 .28 .70 70 .0155
Viola C 65.2 50 .2 .28 1.30 70 .0155
Viola C 65.2 50 1.0 .126 1.25 70 .0155
500 - 1400 Medieval
1400 - 1600 Renaissance
1600 - 1760 Baroque Monteverdi, Vivaldi, Bach, Handel
1720 - 1770 Galant Gluck
1730 - 1820 Classical Mozart
1780 - 1910 Romantic Beethoven, Brahms, Wagner
1890 - Now Modern Prokofiev, Shostakovich
1567 1643 Monteverdi
1637 1707 Buxtehude
1653 1706 Pachelbel
1659 1695 Purcell
1663 1713 Corelli
1671 1751 Albinoni
1678 1741 Vivaldi
1681 1767 Telemann
1685 1750 Bach
1685 1759 Handel
1732 1809 Haydn
1756 1791 Mozart
1770 1827 Beethoven
1782 1840 Paganini
1797 1828 Schubert
1803 1869 Berlioz
1809 1847 Mendelssohn
1810 1849 Chopin
1810 1856 Schumann
1813 1883 Wagner
1813 1901 Verdi
1833 1897 Brahms
1835 1921 Saint-Saens
1838 1920 Bruch
1840 1893 Tchaikovsky
1841 1904 Dvorak
1858 1924 Puccini
1860 1911 Mahler
1862 1918 Debussy
1864 1949 Strauss
1865 1957 Sibelius
1891 1953 Prokofiev
1906 1975 Shostakovich
1873 1943 Rachmaninov
1882 1971 Stravinsky
1910 1981 Barber
Monteverdi L'Orfeo 1607 First opera
Purcell Dido and Aeneas 1683
Handel Agrippina 1710
Handel Giulio Cesare 1724
Handel Theodora 1750
Gluck Orfeo ed Euridice 1762
Gluck Iphigenie en Tauride 1779
Mozart The Marriage of Figaro 1786
Mozart Don Giovanni 1787
Mozart The Magic Flute 1791
Beethoven Fidelio 1805
Rossini The Barber of Seville 1616
Rossini Othello 1816
Rossini The Thieving Magpie 1817
Rossini William Tell 1829
Wagner The Flying Dutchman 1843
Wagner Tannhauser 1845
Wagner Lohengrin 1850
Verdi Rigoletto 1851
Verdi The Troubadour 1853
Verdi La Traviata 1853
Offenbach Orpheus in the Underworld 1858
Berlioz Les Troyens 1858
Wagner Tristan and Isolde 1865
Verdi Don Carlos 1867
Wagner Das Rheingold 1869 Ring cycle 1
Wagner Die Walkure 1870 Ring cycle 2
Verdi Aida 1871
Strauss II Die Fledermaus 1874
Bizet Carmen 1875
Wagner Siegfried 1876 Ring cycle 3
Wagner Gotterdammerung 1876 Ring cycle 4
Saint-Saens Samson and Delilah 1877
Tchaikovsky Eugene Onegin 1879
Offenbach The Tales of Hoffman 1881
Wagner Parsifal 1882
Delibes Lakme 1883
Verdi Otello 1887
Humperdinck Hansel and Gretal 1893
Puccini La Boheme 1896
Puccini Tosca 1900
Debussy Pelleas et Melisande 1902
Puccini Madama Butterfly 1904
Strauss Salome 1905
Strauss Elektra 1909
Prokofiev The Love for Three Oranges 1921
Puccini Turandot 1926
Britten Peter Grimes 1945
Bernstein Candide 1956
Williams Star Wars IV 1977
Williams Star Wars V 1980
Williams Raiders of the Lost Ark 1981
Williams Star Wars VI 1983
Williams Star Wars I 1999
Williams Star Wars II 2002
Williams Star Wars III 2005
Williams Star Wars VII 2015
Williams The Sorcerer's Stone 2001
Williams The Prisoner of Azkaban 2004
Goldsmith The Shadow 1994
Goldsmith Alien 1979
Goldsmith Star Trek I 1979
Goldsmith Star Trek V 1989
Goldsmith Total Recall 1990
Goldsmith U.S. Marshals 1998
Horner Star Trek II 1982
Horner Star Trek III 1984
Horner Aliens 1986
Horner Glory 1989
Horner Braveheart 1995
Horner Apollo 13 1995
Horner Titanic 1997
Horner Troy 2004
Horner Avatar 2009
Horner The Amazing Spider-Man 2012
Zimmer The Lion King 1994
Zimmer Crimson Tide 1995
Zimmer The Rock 1996
Zimmer Mission Impossible II 2000
Zimmer Gladiator 2000
Zimmer Pearl Harbor 2001
Zimmer Hannibal 2001
Zimmer Curse of the Black Pearl 2003
Zimmer Batman Begins 2005
Zimmer Dead Man's Chest 2006
Zimmer The Da Vinci Code 2006
Zimmer At World's End 2007
Zimmer The Dark Knight 2008
Zimmer Angels and Demons 2009
Zimmer Sherlock Holmes 2009
Zimmer Inception 2010
Zimmer On Stranger Tides 2011
Zimmer Game of Shadows 2011
Zimmer The Dark Knight Rises 2012
Zimmer Man of Steel 2013
Zimmer The Amazing Spider-Man 2 2014
Zimmer Age of Extinction 2014
Zimmer Interstellar 2014
Zimmer Batman vs. Superman 2016
Kamen X-Men 2000
Davis The Matrix 1999
Doyle Thor 2011
Doyle The Goblet of Fire 2005







-2500 An ensemble of lyres was played in the ancient city of Ur, including
lyres, harps, flutes, and reed instruments.
1000 Bowed instruments first developed, such as the Lyre
1200 The guitar comes into use in Europe
1555 Amati develops the four-string violin
1700 Cristofori develops the first piano, an instrument where the string is
struck by a hammer. Early pianos had 5 octaves
1785 Tourte develops the modern bow
1810 Broadwood develops a 6-octave piano
1820 Broadwood develops a 7-octave piano
1821 Erard develops the double-escapement mechanism for the piano, a
device that permitted repeating a note even if the key had not yet risen
to its maximum vertical position. This facilitated rapid playing
of repeated notes.
1835 Tuba invented
1847 Boehm advances the design of the flute, including a switch from wood to metal
1931 Beauchamp builds the first electric guitar











A harpshichord string is plucked and a piano string is hammered.
A harpsichord can't vary its volume.










Invented the opthalmascope, an instrument for examining the inside of the eye.



This violin, now at the Metropolitan Museum of Art, may have been part
of a set made for the marriage of Philip II of Spain to Elisabeth of Valois in
1559, which would make it one of the earliest known violins in existence.
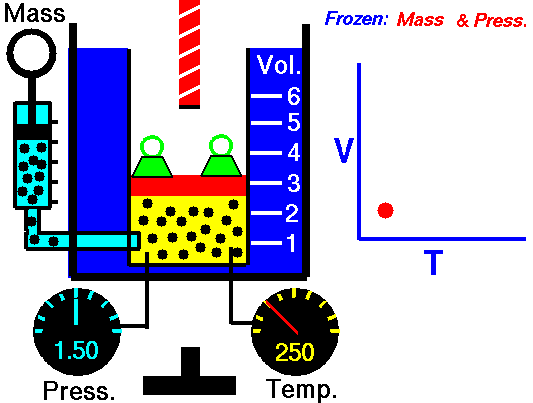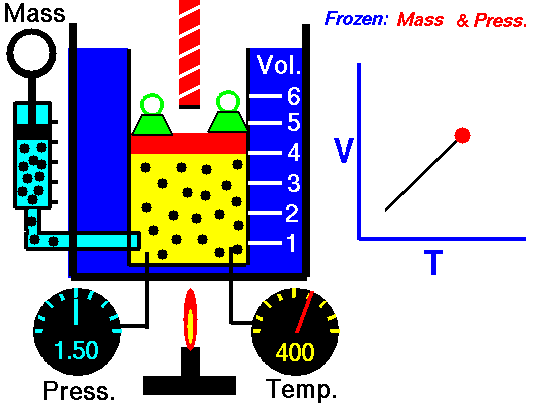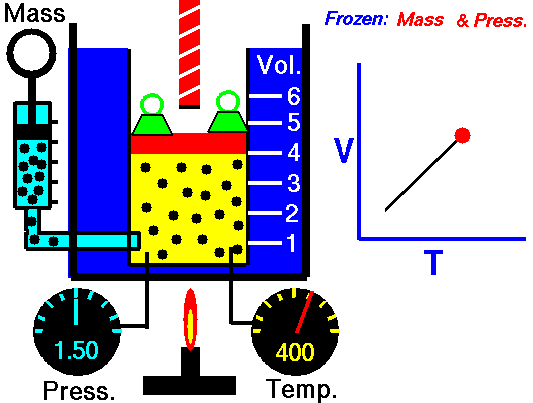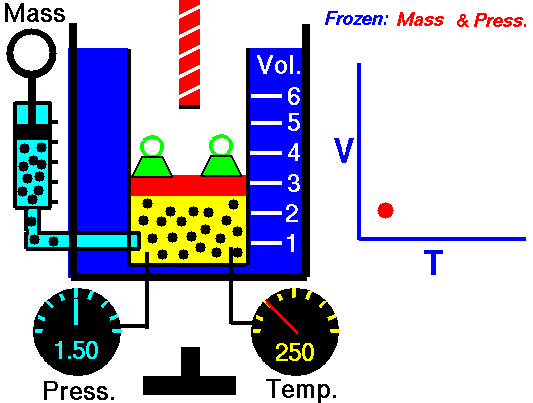
P = Pressure
T = Temperature
Vol= Volume
N = Number of gas molecules within the volume
k = Boltzmann constant
= 1.38*10^-23 Joules/Kelvin
Ideal gas law: (derivation)
P Vol = k T N
If we replace N with Moles then we obtain the form used in chemistry.
N = Moles * 6.62*10^23 (Avogadro's number)
P Vol = 8.3 Moles T
History of the discovery of gas laws:
1660 Boyle law P Vol = Constant at fixed T
1802 Charles law T Vol = Constant at fixed P
1802 Gay-Lussac law T P = Constant at fixed Vol
1811 Avogadro law Vol / N = Constant at fixed T and P
1834 Clapeyron law P Vol / T = Constant combined ideal gas law

M = Mass of a gas molecule
Vthermal= Characteristic thermal speed of gas molecules
E = Mean kinetic energy of a gas molecule
= 1/2 M V^2
Density = N M / Vol
e = Kinetic energy per volume
= N E / Vol
For a system in thermodynamic equilibrium each degree of freedom has
a mean energy of .5 k T.
E = 1.5 k T = .5 M Vthermal^2
The ideal gas law can be written in the form
P Vol = (1/3) N M Vthermal^2
P = (1/3) Density Vthermal^2
Gas simulation at phet.colorado.edu
Sound speed = ( Gamma * Pressure / Density )^{1/2}
where Gamma is the adiabatic constant, equal to 7/5 for air.
This is because diatomic molecules such as nitrogen and oxygen
have an adiabatic constant of 7/5.
Sound speed = ( Gamma Vthermal^2 / 3 )^{1/2}
= .68 Vthermal
The sound speed is proportional to the thermal speed of gas molecules.
Pressure / Density = k T / M
The sound speed is
Sound speed = ( Gamma * Pressure / Density )^{1/2}
= ( Gamma k T / M )^{1/2}
For air, sound speed depends only on temperature.

M in atomic mass units
Helium atom 4
Neon atom 20
Nitrogen molecule 28
Oxygen molecule 32
Argon atom 40
Krypton atom 84
Xenon atom 131
A helium atom has a smaller mass than a nitrogen molecule and hence has a
higher sound speed. This is why the pitch of your voice increases if you
inhale helium. Inhaling xenon makes you sound like Darth Vader.
1635 Gassendi measures the speed of sound to be 478 m/s with 25% error.
1660 Viviani and Borelli produce the first accurate measurement of the speed of
sound, giving a value of 350 m/s.
1660 Hooke's law published. The force on a spring is proportional to the change
in length.
1662 Boyle discovers that for air at fixed temperature,
Pressure * Volume = Constant
1687 Newton publishes the Principia Mathematica, which contains the first analytic
calculation of the speed of sound. The calculated value was 290 m/s.
Newton's calculation was correct if one assumes that a gas behaves like Boyle's
law and Hooke's law.
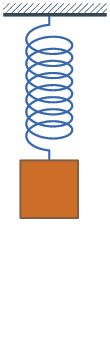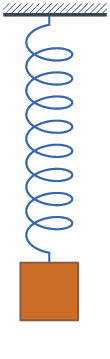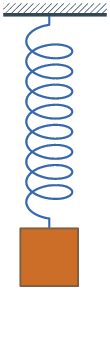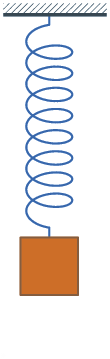

Because of Hooke's law, springs oscillate with a constant frequency.
X = Displacement of a spring
V = Velocity of the spring
A = Acceleration of the spring
F = Force on the spring
M = Spring mass
Q = Spring constant
q = (K/M)^(1/2)
t = time
T = Spring oscillation period
Hooke's law and Newton's law:
F = - Q X = M A
A = - (Q/M) X = - q^2 X
This equation is solved with
X = sin(q t)
V = q cos(q t)
A = -q^2 sin(q t) = - q^2 X
The oscillation period of the spring is
T = 2 Pi / q
= 2 Pi (M/Q)^(1/2)
According to Boyle's law, a gas functions like a spring and hence a gas oscillates
like a spring. An oscillation in a gas is a sound wave.
For a gas,
P = Pressure
dP = Change in pressure
Vol = Volume
dVol= Change in volume
If you change the volume of a gas according to Boyle's law,
P Vol = Constant
P dVol + Vol dP = 0
dP = - (P/Vol) dVol
The change in pressure is proportional to the change in volume.
This is equivalent to Hooke's law, where pressure takes the role of force
and the change in volume takes the role of displacement of the spring.
This is the mechanism behind sound waves.
In Boyle's law, the change in volume is assumed to be slow so the gas
has time to equilibrate temperature with its surroundings. In this case
the temperature is constant as the volume changes and the change is
"isothermal".
P Vol = Constant
If the change in volume is fast then the walls do work on the molecules,
changing their temperature. If there isn't enough time to equilibrate
temperature with the surroundings then the change is "adiabatic". You can see
this in action with the "Gas" simulation at phet.colorado.edu.
Moving the wall changes the thermal speed of molecules and hence the temperature.
If a gas consists of pointlike particles then
Vol = Volume of the gas
Ek = Total kinetic energy of gas molecules within the volume
E = Total energy of gas molecules within the volume
= Kinetic energy plus the energy from molecular rotation and vibration
dE = Change in energy as the volume changes
P = Pressure
dP = Change in pressure as the volume changes
D = Density
C = Speed of sound in the gas
d = Number of degrees of freedom of a gas molecule
= 3 for a monotomic gas such as Helium
= 5 for a diatomic gas such as nitrogen
G = Adiabatic constant
= 1 + 2/d
= 5/3 for a monatomic gas
= 7/5 for a diatomic gas
k = Boltzmann constant
T = Temperature
The ideal gas law is
P Vol = (2/3) Ek (Derived in www.jaymaron.com/gas/gas.html)
This law is equivalent to the formula that appears in chemistry.
P Vol = Moles R T
For a gas in thermal equilibrium each degree of freedom has a mean energy of
.5 k T. For a gas of pointlike particles (monotomic) there are three degrees of
freedom, one each for motion in the X, Y, and Z direction. In this case d=3.
The mean kinetic energy of each gas molecule is 3 * (.5 k T).
The total mean energy of each gas molecule is also 3 * (.5 k T).
Ek = 3 * (.5 k T)
E = d * (.5 k T)
Ek = (3/d) E
If you change the volume of a gas adiabatically, the walls change the kinetic and
rotational energy of the gas molecules.
dE = -P dVol
The ideal gas law in terms of E instead of Ek is
P Vol = (2/d) E
dP = (2/d) (dE/Vol - E dVol/Vol^2)
= (2/d) [-P dVol/Vol - (d/2) P dVol/Vol]
= -(1+2/d) P dVol/Vol
= - G P dVol/Vol
This equation determines the speed of sound in a gas.
C^2 = G P / D
For air,
P = 1.01e5 Newtons/meter^2
D = 1.2 kg/meter^3
Newton assumed G=1 from Boyle's law and calculated the speed of sound in air to be
C = 290 m/s
The correct value for air is G=7/5, which gives a sound speed of
C = 343 m/s
which is in accord with the measurement.
For a gas, G can be measured by measuring the sound speed. The results are
Helium 5/3 Monatomic molecule
Argon 5/3 Monatonic molecule
Air 7/5 4/5 Nitrogen and 1/5 Oxygen
Oxygen 7/5 Diatomic molecule
Nitrogen 7/5 Diatomic molecule
The fact that G is not equal to 1 was the first solid evidence for the
existence of atoms and it also contained a clue for quantum mechanics. If a
gas is a continuum (like Hooke's law) it has G=1 and if it consists of
pointlike particles (monatonic) it has G=5/3. This explains helium and argon
but not nitrogen and oxygen. Nitrogen and oxygen are diatomic molecules and
their rotational degrees of freedom change Gamma.
Kinetic degrees Rotational degrees Gamma
of freedom of freedom
Monatonic gas 3 0 5/3
Diatomic gas T < 1000 K 3 2 7/5
Diatomic gas, T > 1000 K 3 3 4/3
Quantum mechanics freezes out one of the rotation modes at low temperature.
Without quantum mechanics, diatomic molecules would have Gamma=4/3 at room
temperature.
E = Energy
dE = Change in energy
e = Energy density
Vol= Volume
P = Pressure
The volume expands as the universe expands.
dE = - P dVol
For dark energy, the energy density "e" is constant in space and so
dE = e dVol
Hence,
P = - e
Dark energy has a negative pressure, which means that it behaves differently
from a continuum and from particles.