





 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|
 |
|---|
Section 1: Physics of music (this section)
Section 2: Materials and elasticity
Section 3: Anatomy
Section 4: Music performance
Section 5: Physics
Balance
History of kung fu
Instrument balance
![]() Sword
Angular momentum
Frames of reference
Speed
Eyes
Damage control
Fundamentals
Phase lock
Standard violin technique
Videos
Styles
Sword
Angular momentum
Frames of reference
Speed
Eyes
Damage control
Fundamentals
Phase lock
Standard violin technique
Videos
Styles
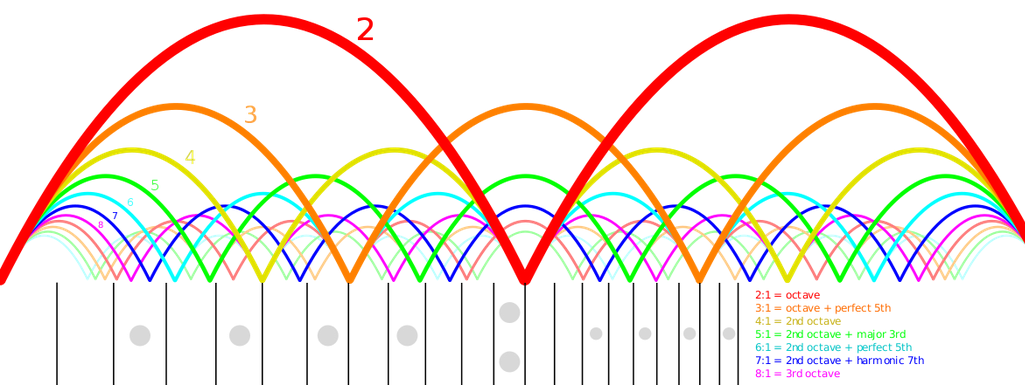
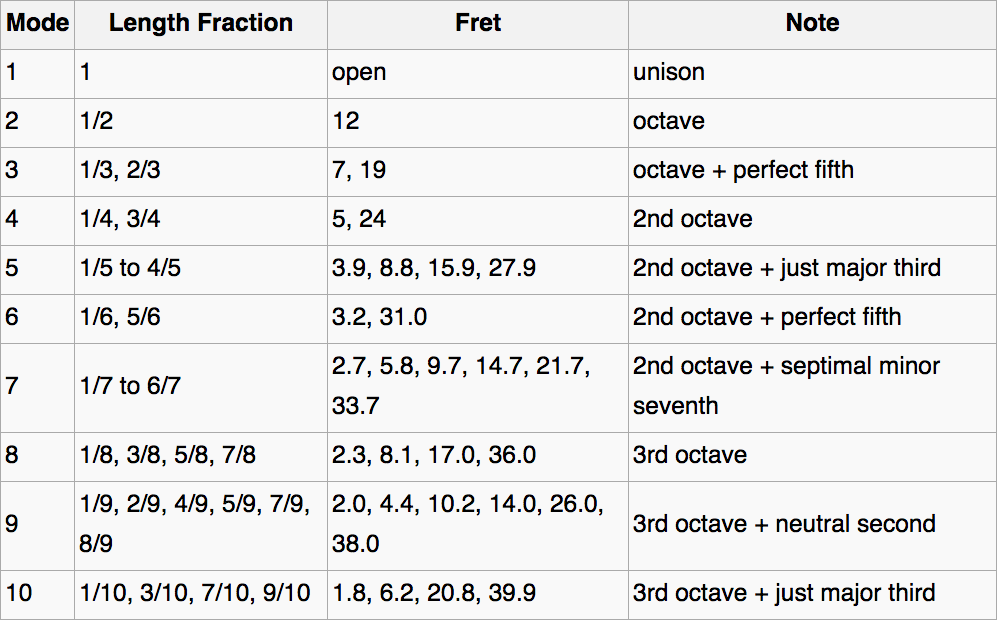
Units Conservation of momentum and energy Angular momentum
 |
 |
|---|---|
 |
 |
|---|---|
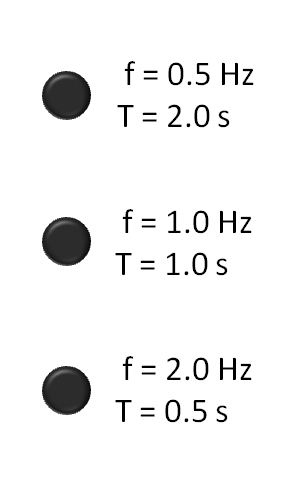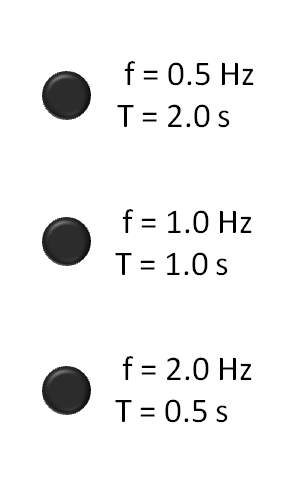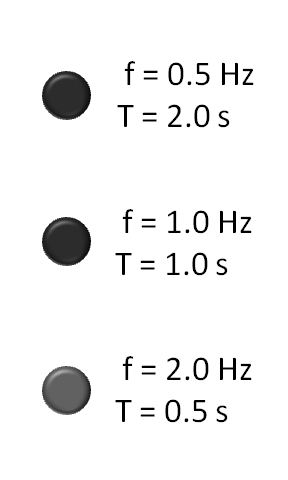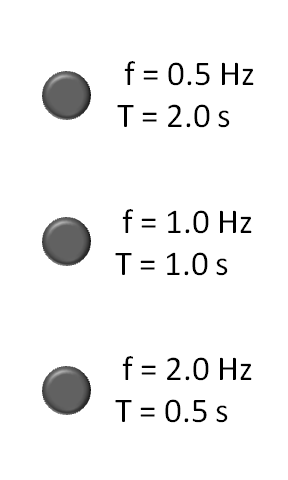 |
|---|
The properties of a wave are
F = Frequency (1/seconds) W = Wavelength (meters) V = Wavespeed (meters/second) T = Period (seconds) (The time it takes for one wavelength to pass by) A = Amplitude (half the distance between the top and bottom crests of the wave)Wave equations:
F W = V F T = 1
 |
|---|
Length of a train car = Wavelength = W = 10 meters Speed of the train = Wavespeed = V = 20 meters/second Cars per second = Frequency = F = 2 Hertz Car time = Period = T = .5 seconds
 |
|---|
Speed of sound at sea level = V = 340 meters/second Frequency of a violin A string = F = 440 Hertz Wavelength of a sound wave = W = .77 meters = W/F Wave period = T = .0023 seconds
 |
|---|
A wave on a string moves at constant speed and reflects at the boundaries.
Frequency of a violin A-string = F = 440 Hertz Length of a violin A-string = L = .32 meters Round trip time up and down the string = T = 2L/V = F-1 =.00227 seconds Speed of a wave on a violin A-string = V = F/(2L) = 688 meters/second
 |
|---|
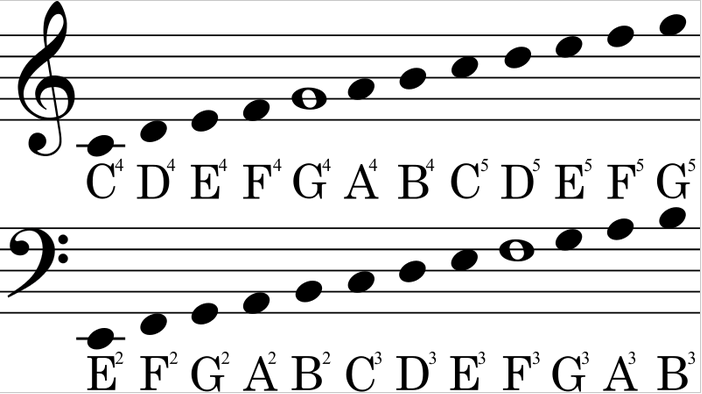
The "A" at the center of the treble clef has a frequency of 440 Hertz. We will use this "A" as a reference. There are 12 notes between this "A" and the "A" an octave above it, where each note is separated by a half step.
Note Note Notes in an Notes in an Name of index letters A-major scale A-minor scale interval 0 A A A Tonic 1 A# or Bb Minor second = Half step 2 B B B Major second = Whole step 3 C C Minor third 4 C# or Db C# Major third 5 D D D Perfect fourth 6 D# or Eb Tritone 7 E E E Minor fifth 8 F F Minor sixth 9 F# or Gb F# Major sixth 10 G G Minor seventh 11 G# or Ab G# Major seventh 12 A A A Octave"A#" stands for "A sharp" and "Bb" stands for "B flat".
The bottom note is the "tonic" and the "interval" is the distance between the tonic and the given note.
When describing intervals we will usually refer to the note index rather than the interval name or the note letter. A change of index of 1 is a half step and a change of index of 2 is a whole step. An octave is 12 half steps.
 |
 |
|---|---|
The choice of "A" for the tonic is arbitrary. We could have used any of the other 11 notes. If the tonic is "D" then the notes in a major and minor scale are:
 |
 |
|---|---|
A chromatic scale contains all 12 notes. A chromatic scale with a tonic of "C" looks like:
 |
|---|
Wikipedia: Clefs Musical intervals Chromatic scale Major scale Minor scale Octave Perfect fifth Perfect fourth
If two notes are played at the same time then we hear the sum of the waveforms.
If two notes are played such that the frequency of the high note is twice that of the low note then this is an octave. The wavelength of the high note is half that of the low note.
Color Frequency Wavelength Orange 220 Hertz 1 Red 440 Hertz 1/2Because the red and orange waves match up after a distance of 1 the blue note is periodic. This makes it easy for your ear to process.
 |
|---|
If we double both frequencies then it also sounds like an octave. The shape of the blue wave is preserved.
 |
|---|
Color Frequency Wavelength Orange 440 Hertz 1/2 Red 880 Hertz 1/4When listening to two simultaneous pitches our ear is sensitive to the frequency ratio. For both of the above octaves the ratio of the high frequency to the low frequency is 2.
440 / 220 = 2 880 / 440 = 2If we are talking about frequency ratios and not absolute frequencies then for simplicity we can set the bottom frequency equal to 1. Hence for an octave,
F1 = 1 F2 = 2For a fifth (playing an A and an E),
F1 = 1 F2 = 3/2
 |
|---|
 |
|---|
 |
|---|
 |
|---|
 |
|---|
 |
|---|
The octave, fifth, fourth, major third, and minor third are all periodic and sound harmonious.
The tritone is not periodic and sounds dissonant.
If two notes in an interval have frequencies such that
Frequency of top note / Frequency of bottom note = I / J where I and J are small integersthen the summed note will be periodic. The smaller the integers I and J, the more noticeable the periodicity and the more harmonious the interval. This is why fifths and fourths sound more resonant than thirds.
If the note "A" is played together with the notes of the 12-tone scale the result is
Note Interval Frequency Result A Unison 1.000 Strongly resonant Bb Minor second 1.059 Dissonant B Major second 9/8 Resonance barely noticeable C Minor third 6/5 Weakly resonant C# Major third 5/4 Weakly resonant D Fourth 4/3 Strongly resonant Eb Tritone 1.414 Dissonant E Fifth 3/2 Strongly resonant F Minor sixth 1.587 Weakly resonant F# Major sixth 5/3 Weakly resonant G Minor seventh 1.587 Dissonant G# Major seventh 1.888 Dissonant A Octave 2 Strongly resonantThe notes {Bb, B, Eb, G, Ab} cannot be expressed as a ratio of small integers and so they sound dissonant when played together with an A.
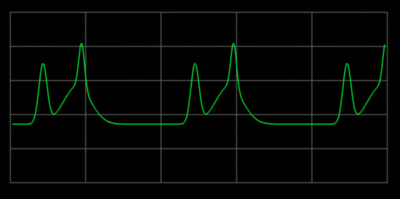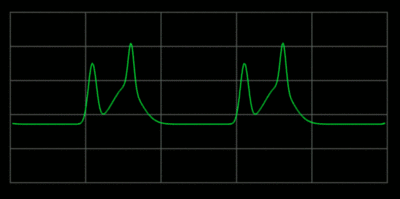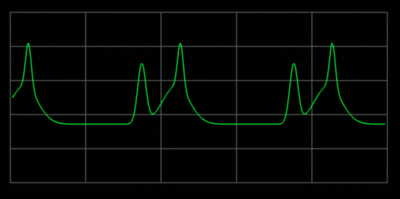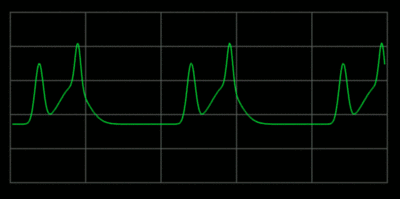
If two notes are out of tune they produce dissonant beat frequencies.
Frequency of note #1 = F1 Frequency of note #2 = F2 Beat frequency = Fb = F2 - F1For the beats to not be noticeable, Fb has to be less than one Hertz. On the E string there is little margin for error. Vibrato is often used to cover up the beat frequencies.
 |
|---|
 |
|---|
 |
|---|
 |
|---|
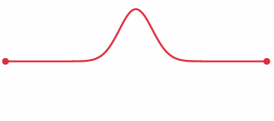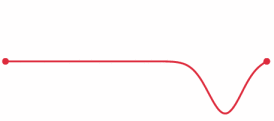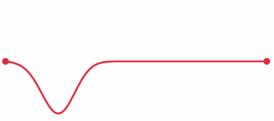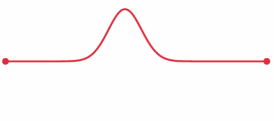
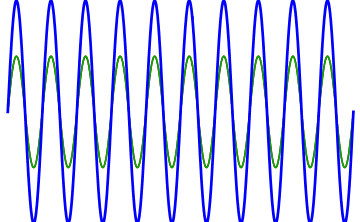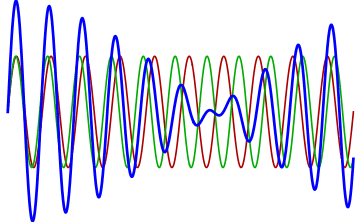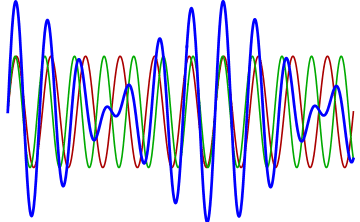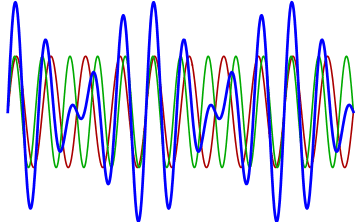
The more out of tune the note, the more pronounced the beat frequencies. In the first figure, the notes are in tune and no beat frequencies are produced.
If you play an octave out of tune you also get beat frequencies.
 |
|---|
 |
|---|
 |
|---|
If you want to divide the octave into 12 pitches such that the interval between each pitch is equal, the pitches have the form
I = An integer where 0 corresponds to the tonic and 12 corresponds to the octave. F = Frequency of the pitches = 2I/12For the tonic,
F = 20/12 = 1For the octave,
F = 212/12 = 2The frequency ratio between two adjacent pitches is
Frequency ratio = 2(I+1)/12 / 2I/12
= 21/12
= 1.059
which is independent of I.
 |
|---|
Note Index Interval Equal Just tuning Major Minor Pythagorean Cents
tuning scale scale tuning
A 0 Unison 1.000 1.000 = 1/1 * * 1/1 = 1.000 0
Bflat 1 Minor second 1.059 256/243 = 1.053
B 2 Major second 1.122 1.125 = 9/8 * * 9/8 = 1.125 + 9
C 3 Minor third 1.189 1.200 = 6/5 * 32/27 = 1.185 -16
C# 4 Major third 1.260 1.250 = 5/4 * 81/64 = 1.266 +14
D 5 Fourth 1.335 1.333 = 4/3 * * 4/3 = 1.333 + 2
Eflat 6 Tritone 1.414 729/512 = 1.424
E 7 Fifth 1.498 1.500 = 3/2 * * 3/2 = 1.500 - 2
F 8 Minor sixth 1.587 1.600 = 8/5 * 128/81 = 1.580 -14
F# 9 Sixth 1.682 1.667 = 5/3 * 27/16 = 1.688 +16
G 10 Minor seventh 1.782 * 16/9 = 1.778
Aflat 11 Major seventh 1.888 * 243/128 = 1.898
A 12 Octave 2.000 2.000 = 2/1 * * 2/1 = 2.000 0
In equal tuning, the frequency ratio of an interval is
Frequency ratio = 2(Index/12) Where "Index" is an integerEqual tuning is based on equal frequency ratios. Just tuning adjusts the frequencies to correspond to the nearest convenient integer ratio. For example, in equal tuning, the frequency ratio of a fifth is 1.498 and just tuning changes it to 1.500 = 3/2.
For the 12 tone scale, equal tuning and just tuning are nearly identical.
The major and minor modes favor the resonant notes.
Cents refers to the difference between just tuning and equal tuning. 100 Cents corresponds to a half step and 1 cent corresponds to .01 half steps.
In the 6th century BCE, Pythagoras developed a 12-tone scale based on the
ratios 2/1 and 3/2. This tuning was widely used until the 16th century CE.
Pythagorean tuning gives good results for fourths and fifths but poor results
for thirds, and it is not possible to write contrapuntal music.
In the 2nd century CE, Ptolemy developed the "major scale", based on the frequency
ratios 2/1, 3/2, 4/3, and 5/4. This scale allows for consonant thirds.
J.S. Bach tuned his own harpsichords and clavichords and he customized the tuning to
work in all 24 keys ("well temperament"). He demonstrated its effectiveness
in his 1722 work "The Well Tempered Clavier".
Just tuning is based on integer ratios and equal tuning is based on logarithms,
and there is no direct connection between them. By freak mathematical
coincidence, 12-tone equal tuning gives a set of notes that are nearly
identical to those for just tuning (see the above table). The correspondence
is close, but not exact, and violinists use a compromise between just and equal
tuning that is highly situation dependent. The Bach Chaconne in D minor is a
tour de force of just intonation.
The synthesis of just and equal tuning offers rich contrapuntal possibilities,
as was explored during the Baroque age by composers such as Vivaldi, Bach, and
Handel.
The notes for 12-tone equal temperament coincide well with the note of just
intonaton.
The most resonant notes in the 12-tone equal temperament scale are the fourth
and the fifth and these are particularly close to their just-intonation
counterparts.
The frequency ratio between a fourth and a fifth in just-temperament is
Tunings exist that use numbers different from 12, such as for Indian, Thai, and Arabic
music. These tunings can generate exotic melodic structure but they are less useful
for harmony than the 12-tone scale.
The 12-tone scale is natural in the sense that it doesn't have any "free parameters".
The choice of the number "12" emerged naturally from the positions of the
resonant notes. It is also "fortuitous" in that the values of Z are so small.
Soccer is an example of a "natural sport". The rules are simple and if you change
the parameters (such as field size, number of players, etc) the game is essentially
the same.
American football requires "fine tuning". In order for the sport to make sense
you need a large rulebook. It also has lots of "free parameters" because there
are many different ways the rules could be constructed.
The chess player Edward Lasker once said:
"While the Baroque rules of Chess could only have been created by humans, the
rules of Go are so elegant, organic, and rigorously logical that if intelligent
life forms exist elsewhere in the universe, they almost certainly play Go."
The rules of chess are an example of "fine tuning" and there are lots of
free parameters (the moves allowed by each piece).
Dfferences in pitch are often expressed in "cents".
A half step corresponds to 100 cents and the limit of human sensitivity is
10 cents. The above table on just and equal tuning shows the difference
between the two systems in cents.
The frequency ratio of a half step is
For example, for the notes on an A-string with a frequency of 440 Hertz,
If we start from a frequency of 880 Hertz then the frequencies are
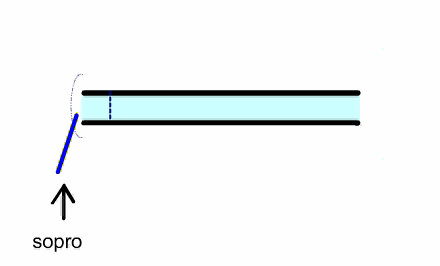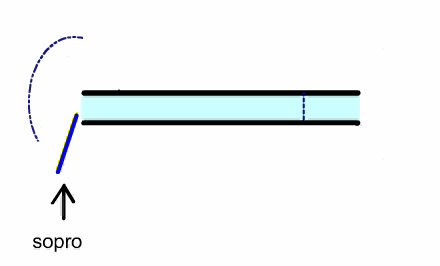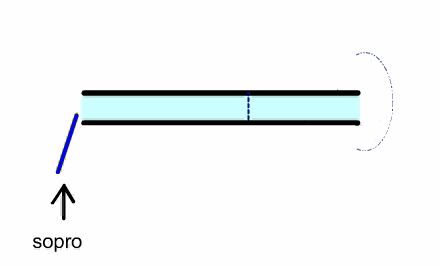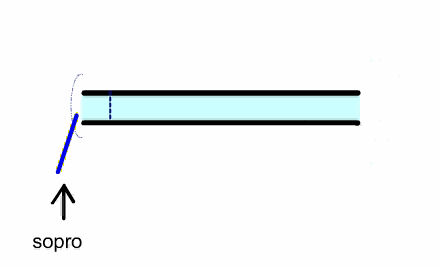
In a reed instrument, a puff of air enters the pipe, which closes the
reed because of the Bernoulli effect. A pressure pulse travels to the other
and and back and when it returns it opens the reed, allowing another puff of
air to enter the pipe and repeat the cycle.
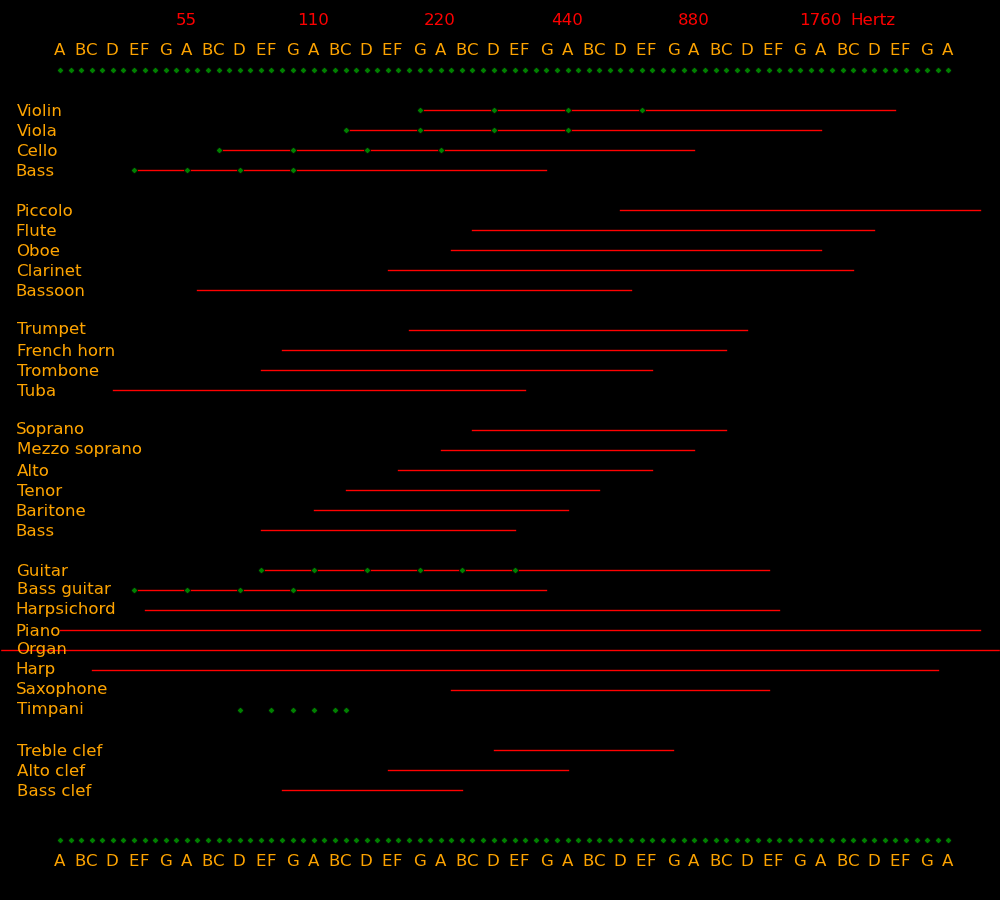
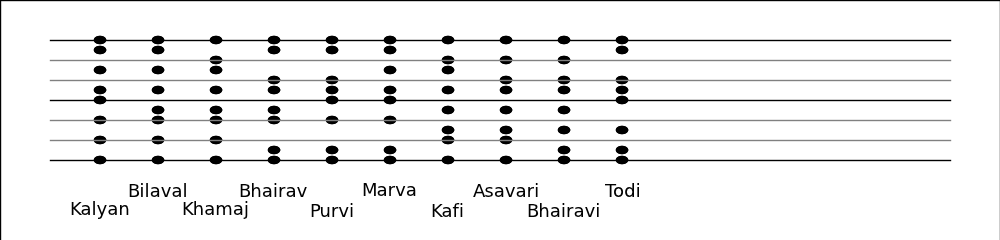
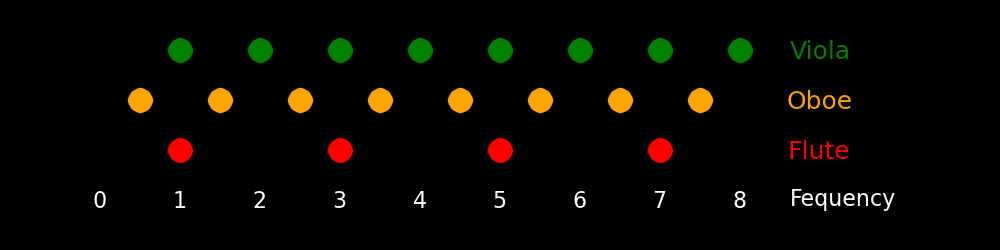
Green dots indicate the frequencies of open strings.
An orchestral bass and a bass guitar have the same string tunings.
The range of organs is variable and typically extends beyond the piano in both
the high and low direction.
Violins, violas, and cellos are tuned in fifths. String basses, guitars, and bass
guitars are tuned in fourths. Pianos are tuned with equal tuning.
A bass guitar is tuned like a string bass.
The viola is the largest instrument for which one can comfortably play
an octave, for example by playing a D on the C-string with the first finger
and a D on the G-string with the fourth finger. Cellists have to shift to
reach the D on the G-string.
According to legend Bach used a supersized viola, the
"Viola Pomposa"
Singers typically have a range of 2 octaves. The low note for each instrument is:
For guitars, tenors, basses, and bass guitars, the tuning is an octave lower
than written.
The viola d'amore has 7 playing strings and 6 resonance strings.
A sitar has 6 or 7 playing strings and 11 or more sympathetic strings.
There is no standard tuning for sitar strings. An example tuning is to set the
playing strings to {C, C, G, C, G, C, F}
and the sympathetic strings to {C, B, A, G, F, E, E, D, C, B, C}
The fret positions can be tuned.
The bridge is curved so that the contact point between the string and the bridge
is not sharp, which has the effect of transferring energy between the string modes.
The surbahar is typically tuned 2 to 5 whole steps below the sitar.
The tanpura does not play melody but rather supports and sustains the melody of
another instrument or singer by providing a continuous harmonic drone.
Guitars frets are set by equal tuning.
The frequency of a note depends on context.
Suppose a set of viola strings is tuned in fifths so that the frequencies are
If the note "E" is chosen to resonate with the G-string its frequency is
The notes in an A-minor mode are
If the notes of the minor scale are arranged depicting the whole and
half steps then it looks like:
The minor mode has the following properties:
There are no instances of 2 half-steps in a row.
A major scale has the same properties. The notes in a major scale look like:
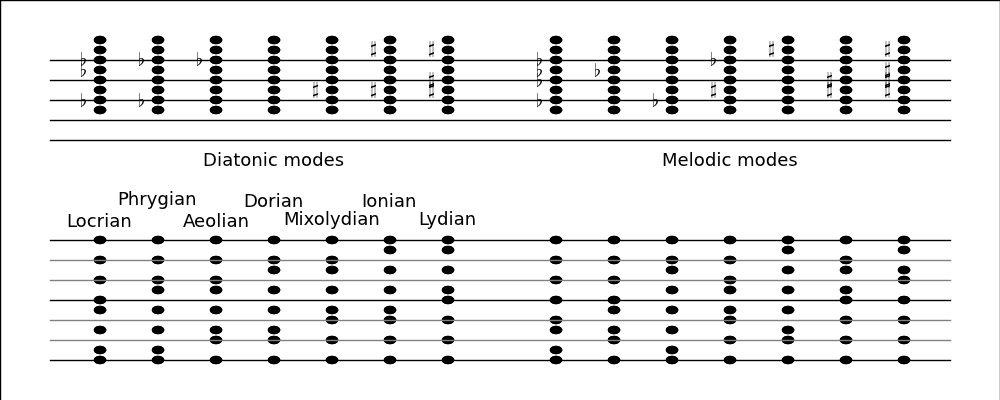
A set of 7 diatonic scales (or "modes") follow from a compact and natural
set of definitions.
k
A diatonic scale consists of a set of notes such that:
This implies:
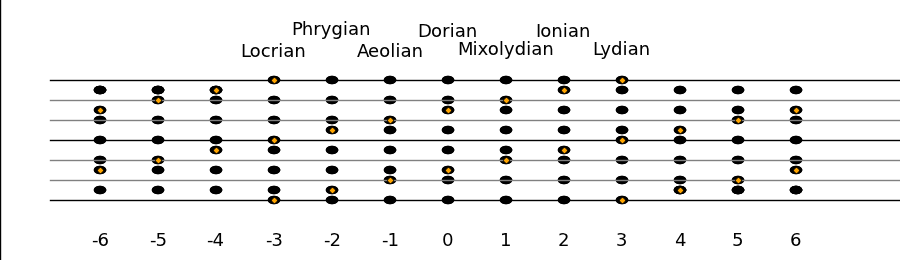
The first seven modes in this figure are the diatonic modes.
The upper staff is a standard treble clef and the bottom note in each mode
is an "A". The Aeolian mode corresponds to the minor mode and the
Ionian mode corresponds to the major mode. In addition to the major and minor
modes there are 5 additional modes.
The modes are ordered so that they grow progressively "sharper" as you move to
the right.
Each mode differs by exactly one note from its adjacent modes.
The lower staff is a "geometric clef" where the vertical position of each note
corresponds to its pitch. The bottom line is the tonic, the top line is the
octave, and the middle line is the tritone. Adjacent lines are separated by a
whole step. This representation is designed to visually bring out the pitch of
each note. In the leftward diatonic modes the notes are shifted toward the
tonic and the rightward diatonic modes the notes are shifted toward the octave.
Equivalently, we can define an infinite sequence of whole and half
steps where the notes look like
This can be thought of as a "sequence of tritone avoidance" since
it contains only 1 instance of 3 consecutive whole steps.
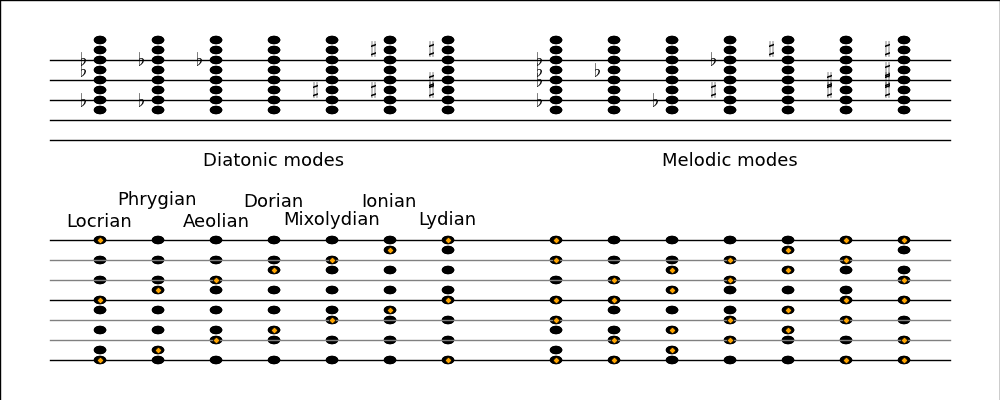
In the following table an orange dot indicates a note involved in a tritone.
The Dorian mode is symmetric under inversion.
The Mixolydian, Dorian, and Aeolian modes are at the center
because their fourths and fifths are not part of a tritone. The Lydian and
Locrian modes are at the edges because they are missing either a major fourth
or a major fifth, the two most resonant notes with the tonic.
For an instrument tuned in fourths, transposing up one string corresponds to
transposing down one mode.
In the diatonic modes there must be at least 2 whole steps separating each half
step. If we relax this condition and allow half steps to be separated by only
one whole step then another set of modes appears with the sequence:
This sequence has 7 unique choices of tonic hence there are 7 modes, the
"melodic modes". They contain 2 tritones whereas the diatonic modes contain 1.
The melodic modes can be arranged into a natural sequence that parallels the
diatonic modes. The melodic modes are depicted in the above figure, which is
equivalent to the table below.
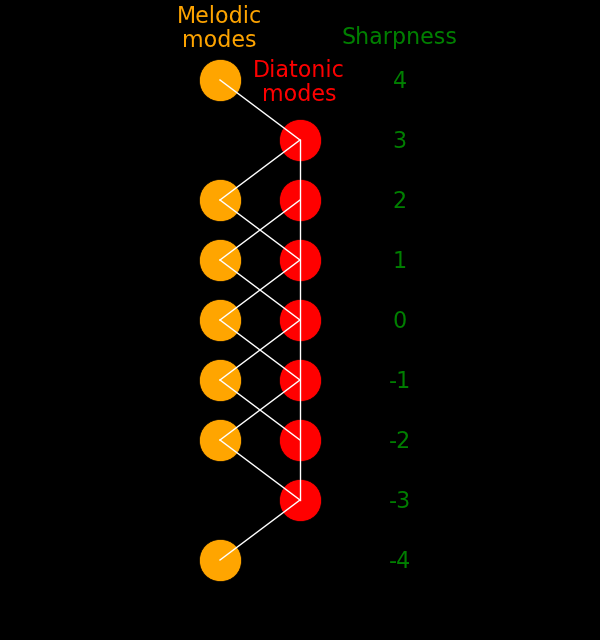
"Sharpness" reflects whether the notes are stacked toward the octave (lots of
sharps, or positive sharpness) or toward the tonic (lots of flats, or negative
sharpness).
If the notes in a mode are assigned integers I where I=0 corresponds to the tonic
and I=12 corresponds to the octave, the sharpness is
To move from a melodic mode to an adjacent melodic mode you need to change 2 notes.
The melodic modes have a natural ordering that parallels the diatonic modes. The
melodic modes can be thought of as alternate pathways for shifting between
diatonic modes.
This figure shows the connectivity between modes.
White lines connect modes that are one note apart.
If you change one note in a mode then you change the
sharpness, which is why there are no horizontal lines in the figure.
If you start from the key of "A" and transpose up a fifth then you are the key
of "E", and transposing down a fifth puts you in the key of "D". The interval
of a "fifth" forms a sequence which repeats itself after 12 intervals. The
following sequence starts at the bottom at "A" and rises in fifths until at the
top it it returns to "A".
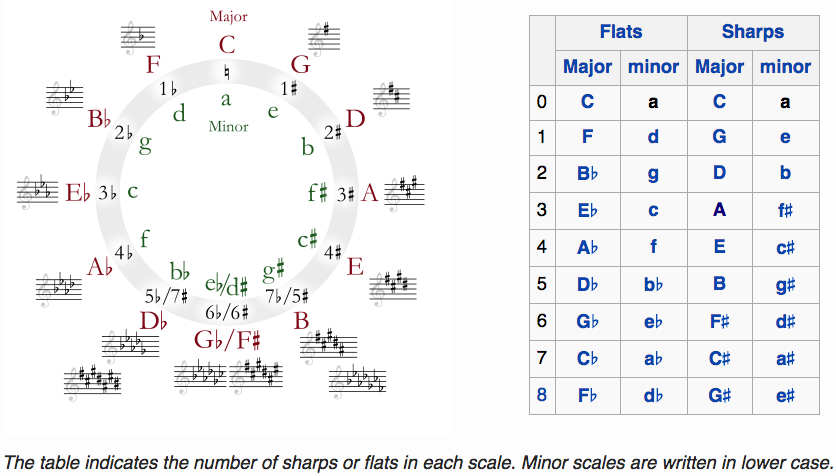
This is the circle of fifths expressed as key signatures on a treble clef.
Major keys are in red capital letters and minor keys are in green lower-case
letters. The keys of A-minor and C-major are at the top of the circle because
they have no sharps or flats. At the bottom of the circle, E flat is
equivalent to D sharp.
The mode "A minor" has tonic "A" and sharpness "-1".
Raising the tonic by a fifth to "E" while keeping the notes unchanged
produces a mode with sharpness "-2".
Lowering the tonic by a fifth to "D" while keeping the notes unchanged
produces a mode with sharpness "0".
In general, transposing up a fifth is equivalent to increasing the sharpness
by 1 and transposing down a fifth is equivalent to decreasing the sharpenss by
1. The following figure expresses this equivalence.
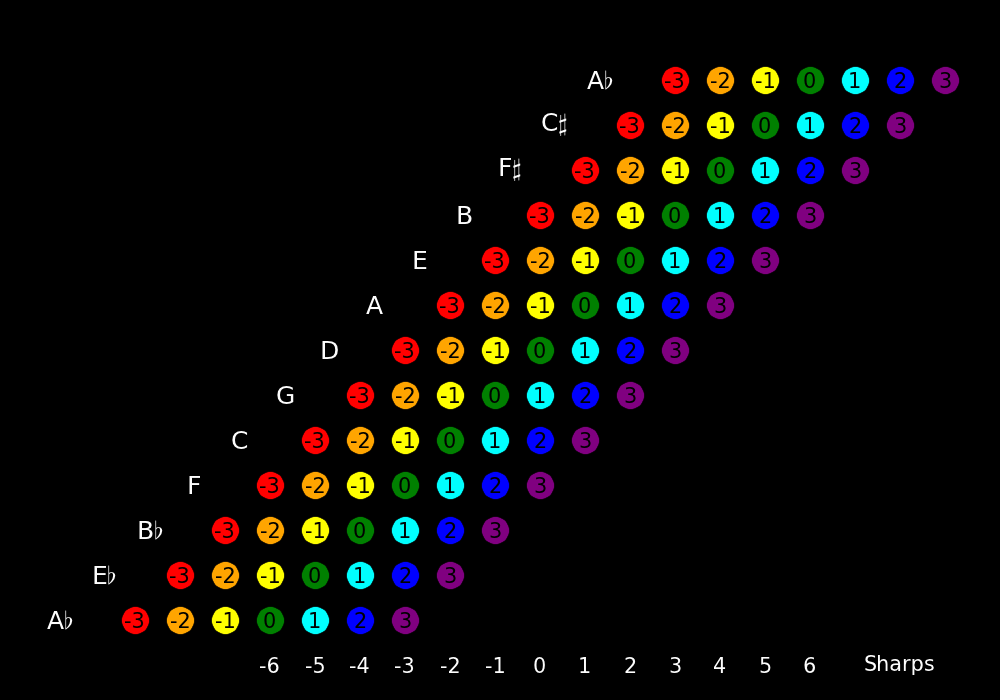
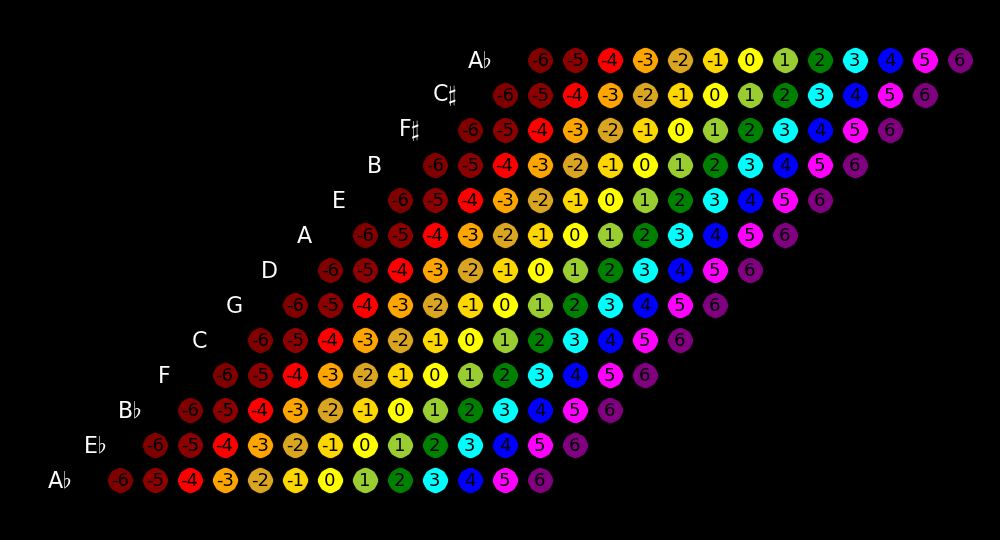
Each row corresponds to a choice of tonic and is labeled with white letters.
Going up by 1 row corresponds to raising the tonic by a fifth.
The top row is identical to the bottom row.
Each tonic has 7 diatonic modes arranged horizontally by sharpness. Modes with
sharpness "-3" are red, modes with sharpness "-2" are orange, etc. Minor modes
are yellow and major modes are blue.
"Sharps" indicates the numbers of sharps that are written on the clef (negative
sharps corresponds to flats). Every mode in the same column has the same number
of sharps on the clef.
This figure contains all possible diatonic modes with all possible tonics.
All modes in the same column have the same notes.
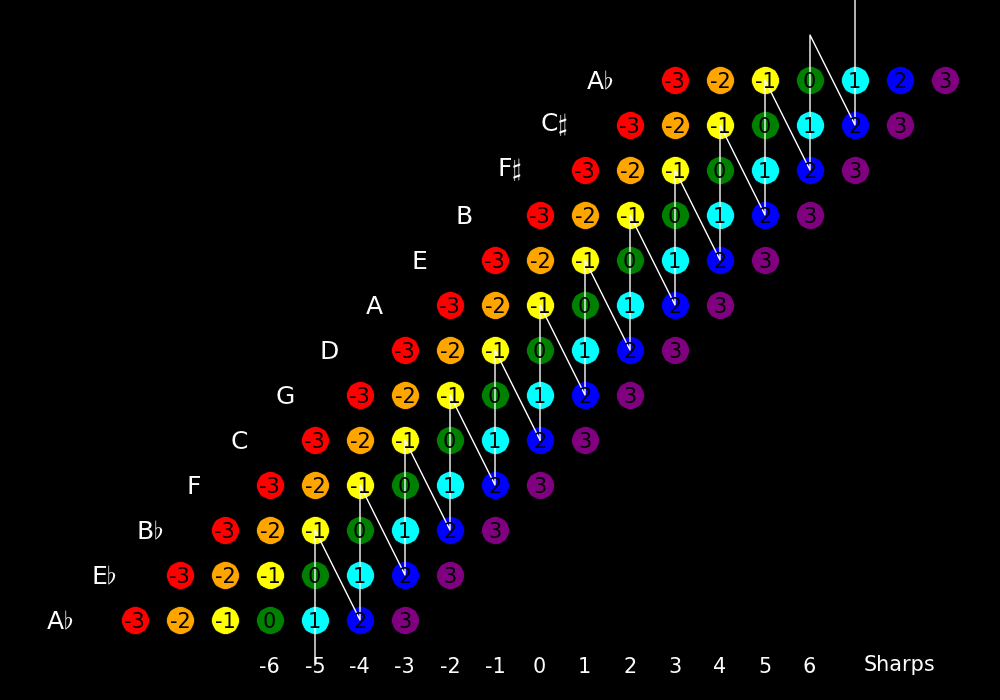
Transposing up a fifth corresponds to moving up one dot and transposing down a
fifth corresponds to moving down one dot.
Increasing the sharpness by 1 corresponds to moving right one dot and decreasing
the sharpness by 1 corresponds to moving left one dot.
Violins are tuned in fifths and can conveniently transpose in fifths.
Guitars are tuned and fourths and can conveniently transpose in fourths.
Transposing up a fifth corresponds to transposing down a fourth.
If you start from a minor mode and increase the tonic by 3 half
steps then you arrive at a major mode with the same notes.
For example, C-major is the "relative major" of A-minor and A-minor is the
"relative minor" of C-major.
Chopin's "24 Preludes, Op. 28" for piano covers all 12 major and minor keys by
circumnavigating the circle of fifths. The keys are ordered as
C-major
The clef is designed so that the core keys have few sharps or flats. Keys
distant from the core keys have lots of sharps or flats.
The core keys are connected harmonically because they have many notes in common
and because they are nearby in terms of fifths. It would be awkward to use a
major key with 4 flats or a minor key with 4 sharps because these are far from
the center from the cluster.
Keys in the Bach sonatas for violin:
Keys in the Vivaldi "L'Estro Armonico concerti for violin"
To be a diatonic mode the mode must contain the tonic. If we relax this condition
then 5 new modes appear and they can be ordered by a tritone sequence. Each mode
has 1 tritone which is denoted by an orange dot.
The modes in the center are the diatonic modes and the modes at the edges are
new modes that don't contain the tonic. Mode "+6" is equivalent to mode "-6".
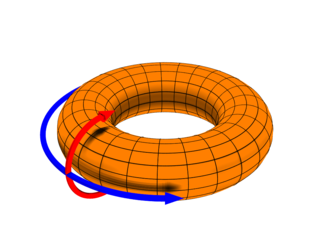
The circle of fifths and the circle of tritones form a torus.
The top row is equivalent to the bottom row and the left edge is equivalent
to the right edge.
The circle of fifths is in the vertical direction and the circle of tritones is
in the horizontal direction.
The following are examples of toruses. A torus can be created by connecting the
opposite edges of a chessboard
Examples of surfaces that are topologically inequivalent.
Let a "doublet" be a set of 2 notes separated by a half step and let a
"triplet" be a sequence of three notes all separated by half steps.
Suppose a pitch set has 8 notes, including the tonic.
The pitch set will have 1, 2, or 3 tritones. Most have more than 1.
If there are no gaps larger than 2, less than 4 doublets, and no triplets,
then the possible sequences are
If triplets are allowed then the following sequence appears, which has 1 tritone
and is asymmetric.
If a wave is linear then it propagates without distortion.
If a wave is linear then waves add linearly and oppositely-traveling waves
pass through each other without distortion.
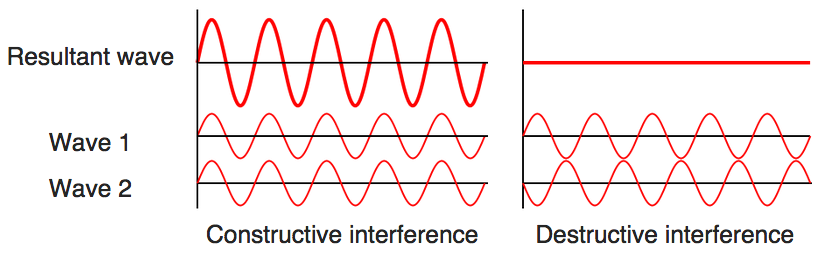
If two waves are added they can interfere constructively or destructively,
depending on the phase between them.
If a speaker system has 2 speakers you can easily sense the interference by
moving around the room. There will be loud spots and quiet spots.
The more speakers, the less noticeable the interference.
Noise-cancelling headphones use the speakers to generate sound that cancels
incoming sound.
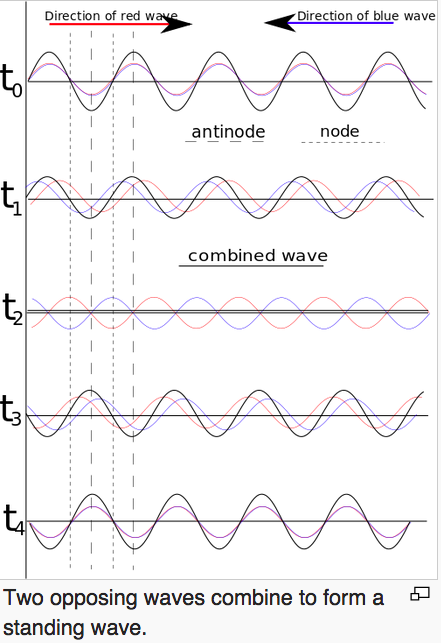
Two waves traveling in opposite directions create a standing wave.
Waves on a string simulation at phet.colorado.edu
For example, the overtones of an A-string with a frequency of 440 Hertz are
Overtone simulation at phet.colorado.edu
An oboe and a clarinet are half-open pipes.
A cantilever has the same overtones as a half-open pipe.
A flute and a bassoon are pipes that are open at both ends and the overtones
are plotted in the figure above. In this case the overtones have twice the
frequency as those for a half-open pipe.
A closed pipe doesn't produce much sound. There are no instruments that are
closed pipes. A muted wind or bass instrument can be like a closed pipe.
Modes 1 through 5 for a closed pipe.
An oboe is a half-open pipe (open at one end), a flute is an open pipe (open at both
ends), and a string behaves like a pipe that is closed at both ends.
If a violin, an oboe, and a flute are all playing a note with 440 Hertz then the
overtones are
The fundamental mode is at the upper left. The number underneath each mode is
the frequency relative to the fundamental mode. The frequencies are not
integer ratios.
In general, overtones of a 1D resonator are integer multiples of the fundamental
frequency and overtones of a 2D resonator are not.
Wikipedia: Virations of a circular membrane
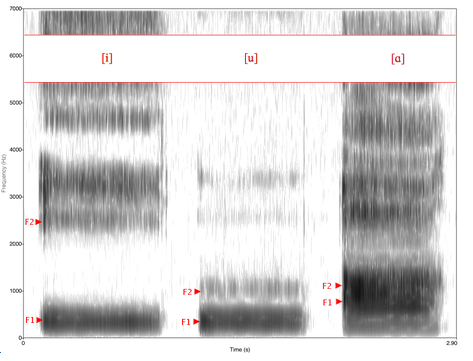
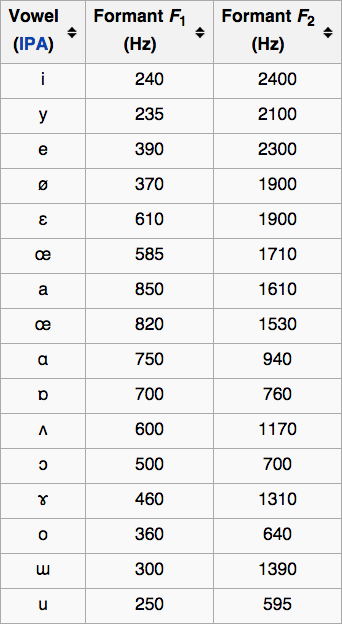
A "formant" is a vocal resonance. Vowels can be identified by their
characteristic mode frequencies.
Standing waves on a string have the form
Suppose a resonator has multiple dimensions. For example, a square is like a
2D string and a cube is like a 3D string. If a resonator consists of a
cubical volume of air then the modes are
Orange dots correspond to (Nx,Ny) pairs and the length of the red lines corresponds
to N.
The modes of a 3D cube are
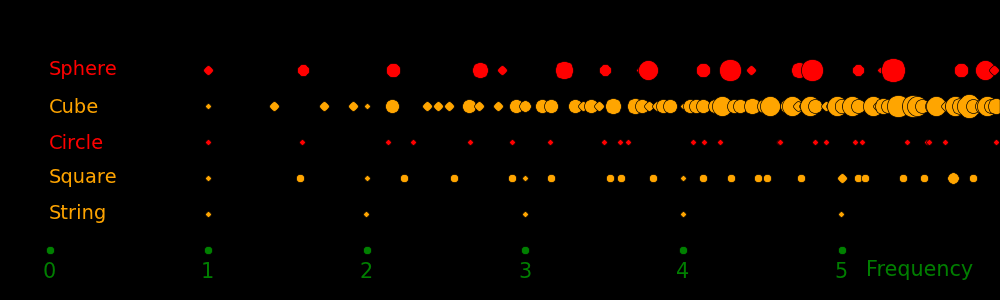
These are the mode frequencies for various resonators, with the frequencies
normalized so that the fundamental frequency is unity. The size of each dot is
equal to the square root of the number of modes at that frequency.
"String", "square", and "cube" correspond to the resonators discussed above
and "circle" and "sphere" are discussed below.
As the dimensionality increases the number of modes increases. Singing
involves a 3D resonator, which is why there are so many vocal formants.
The 2D resonators (square and circle) have similar spectra
and the 3D resonators (cube and sphere) have similar spectra.
If the dimensionality is larger than 1 then there can be multiple modes with the
same frequency.
For large N we can approximate the number of modes as:
A circular drum and a square drum have similar spectra. The fundamental mode of
a drum is
The following python script calculates the mode frequencies of a drum, normalized
so that the fundamental frequency is 1.
The mode frequencies for a circle and sphere are plotted above.
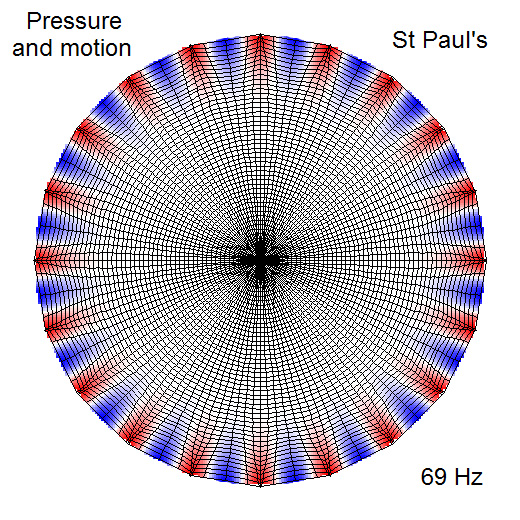
The whispering gallery in St. Paul's Cathedral has the same modes as a
circular drum.
Whispering gallery waves were discovered by Lord Rayleigh in 1878 while he was in
St. Paul's Cathedral.
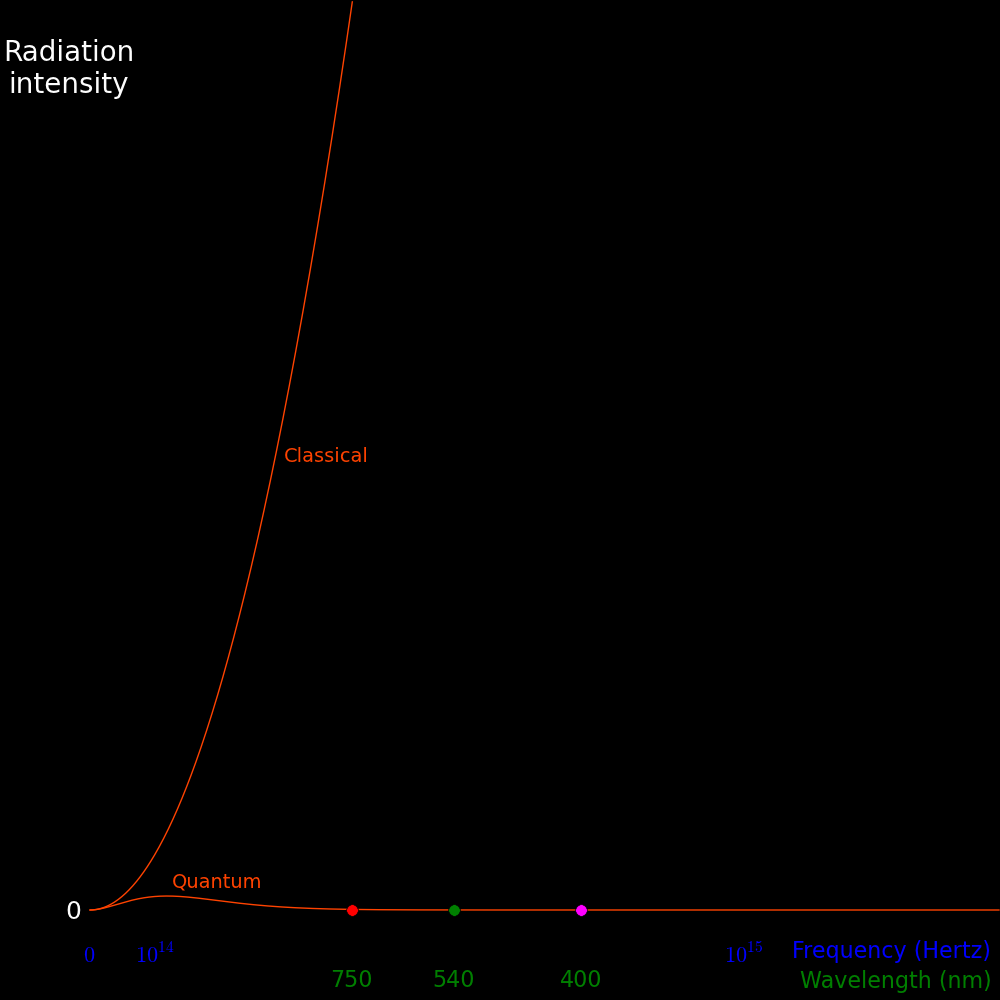
These are the classical and quantum predictions for the radiation intensity at 2000
Kelvin. The divergence of the classical prediction at high frequency is the
"Ultraviolet catastrophy". The problem is resolved by quantum mechanics.
In classical mechanics the thermal energy is the same for each mode and in
quantum mechanics the energy depends on frequency. This eliminates the
divergence at high frequency.
The behavior of the classical blackbody spectrum as a function of frequency
is analogous to the modes of the 3D resonator plotted above.
For a system in thermodynamic equilibrium each degree of freedom has a mean energy
of .5 K T, where K is Boltzmann's constant.
If the modes of a resonator are mechanically connected and if the resonator has
infinite time to evolve then each mode will have the same mean energy.
The larger the dimension, the more modes a resonator has and the more energy it can
store. In 3D the number of modes can be quite large.
Overtones are ubiquitous in vibrating systems. They are usually referred to as
"normal modes".
You can increase the pitch by pulling the string sideways. This increases
the string tension, which increases the wavespeed and hence the frequency.
If you are playing a note on a guitar using a fret, you can change the
frequency of the note by bending the string behind the fret.
The vibration of the string depends on where it is plucked. Plucking the
string close to the bridge enhances the overtones relative to the fundamental
frequency.
A bow produces a sequence of plucks at the fundamental frequency of the string.
The function of the reed is taken up by the vocal chords for singing and by the lips
for brass instruments.
A turbofan compresses the incoming airflow so that it can be combusted with fuel.
In a reed instrument, a puff of air enters the pipe, which closes the reed
because of the Bernoulli effect. A pressure pulse travels to the other and and
back and when it returns it opens the reed, allowing another puff of air to
enter the pipe and repeat the cycle.
Male vocal chords tend to be longer than female vocal chords, giving males a
lower pitch. Male vocal chords range from 1.75 to 2.5 cm and female vocal chords
range from 1.25 to 1.75 cm.
When air passes through the vocal chords the Bernoulli effect closes them.
Further air pressure reopens the vocal chords and the cycle repeats.
The airflow has a triangle-shaped waveform, which because of its sharp edges
generates abundant overtones.
For a lung volume of 2 liters, 4000 Pascals corresponds to an energy of 8 Joules.
Singers, wind, and brass musicians train to deliver a continuous stable
exhalation. String musicians train locking their ribcage in preparation for
delivering a sharp impulse.
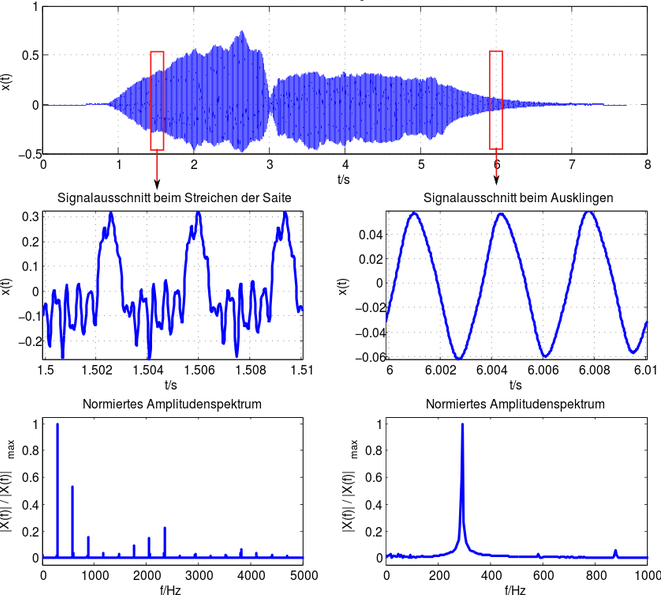
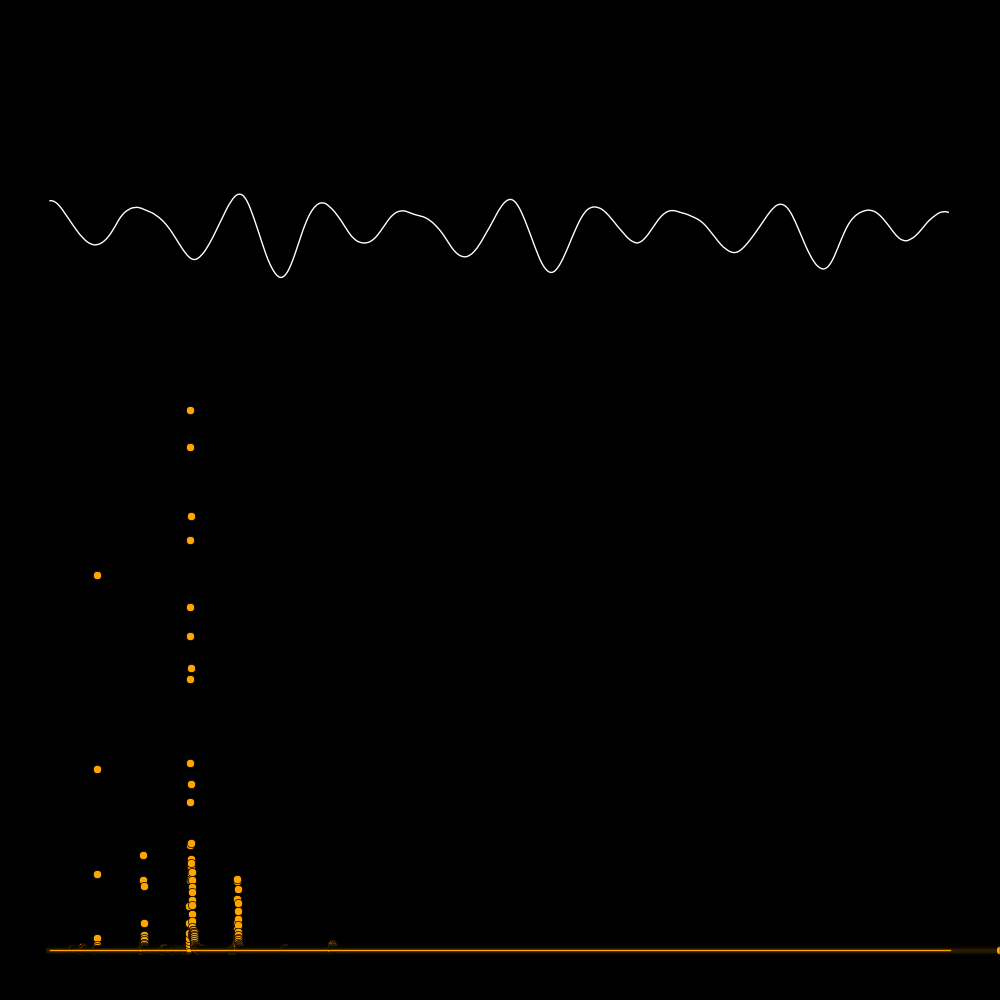
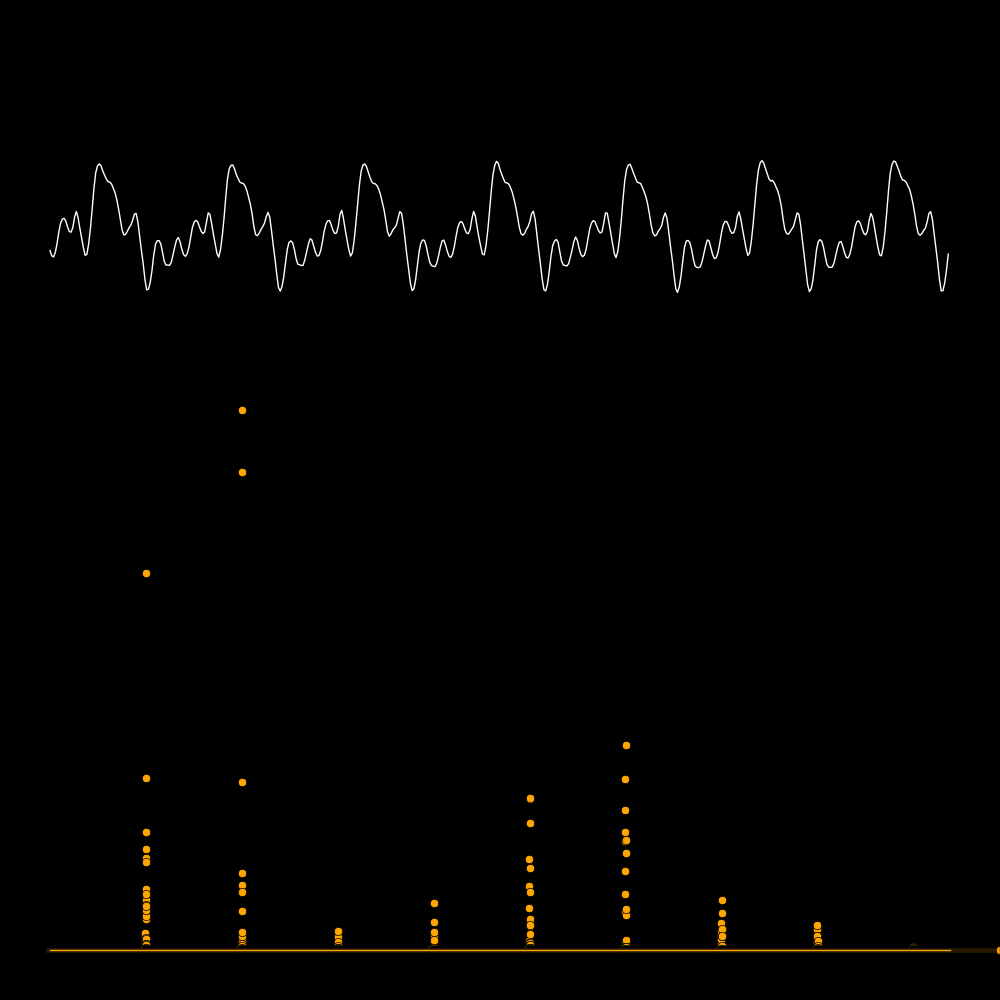
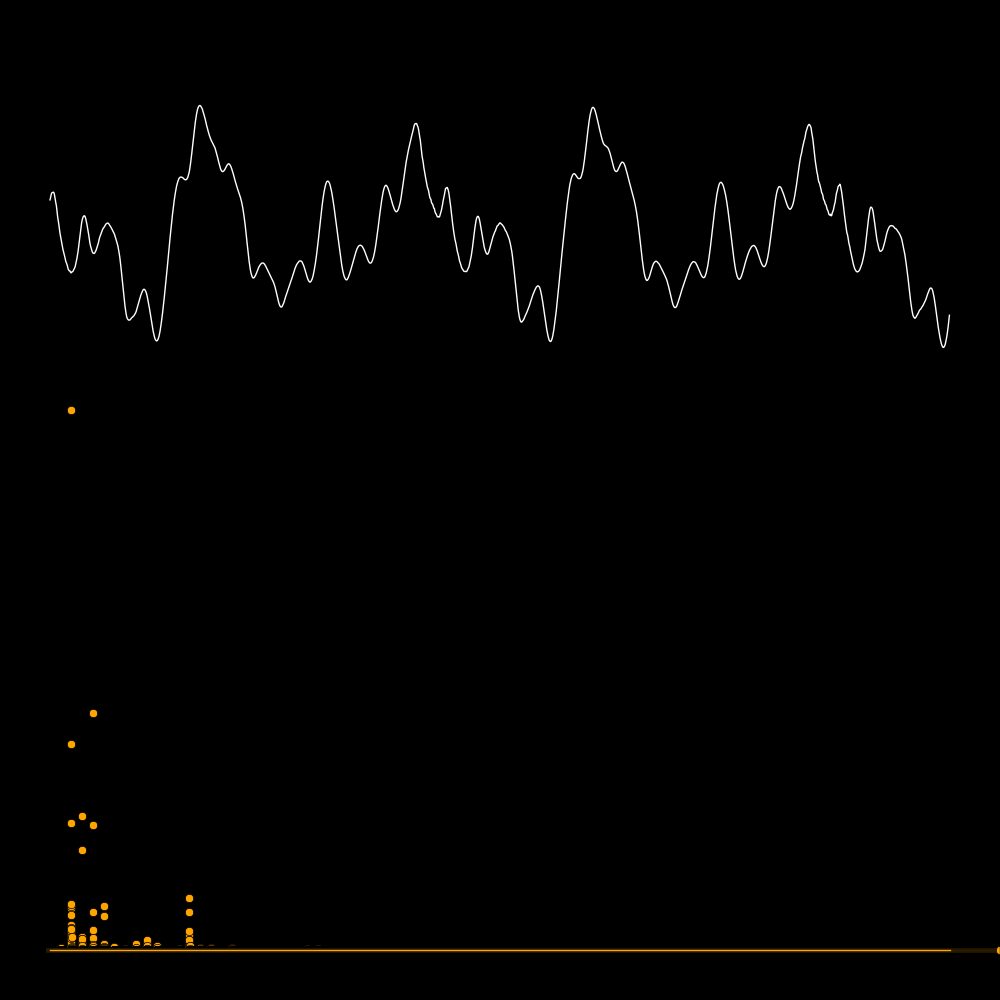
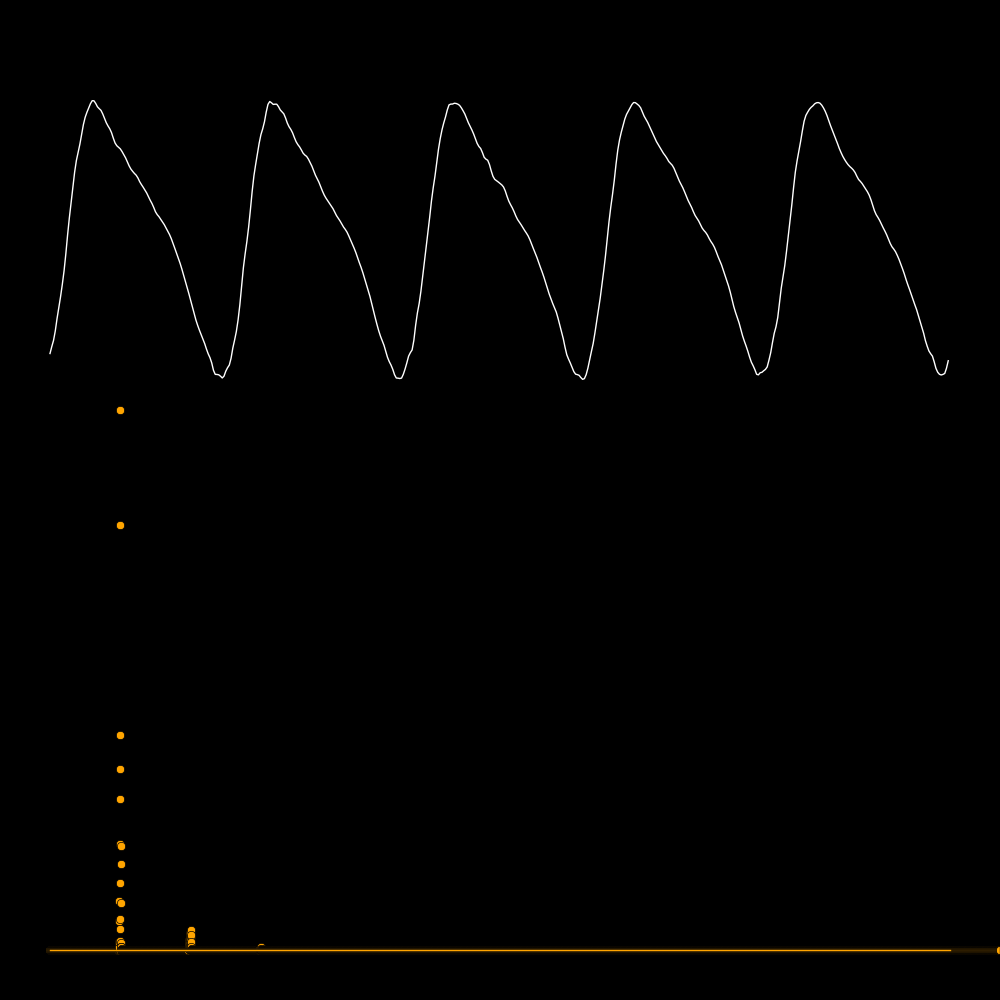
A spectrum tells you the power that is present in each overtone.
The first row is the waveform, the second row is the waveform expanded in time,
and the third row is the spectrum. The spectrum reveals the frequencies
of the overtones. In the panel on the lower left the frequencies are 300, 600, 900,
1200, etc. In the panel on the lower right there are no overtones.
A quality instrument is rich in overtones.
A waveform can be represented as an amplitude as a function of time or as an
amplitude as a function of frequency. A "Fourier transform" allows you to go
back and forth between these representations. A "spectrum" tells you
how much power is present at each frequency.
Fourier transform simulation
at phet.colorado.edu
Music analysis software such as "Audacity" can evaluate the spectrum.
Every instrument produces sound with a different character. The sound can
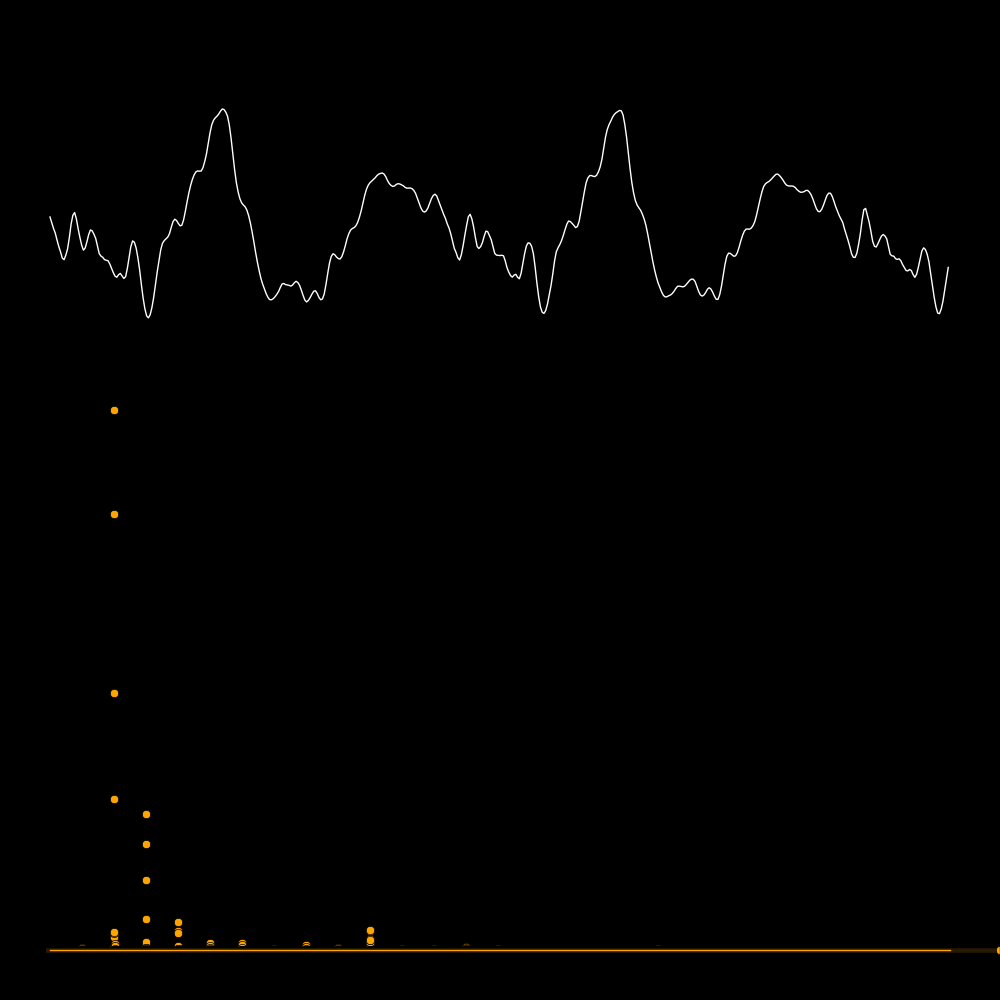
be characterized either with the waveform or with the spectrum
In the following plots the white curve is the waveform and the orange dots are
the spectrum.
Suppose a microphone samples a wave at fixed time intervals. The white curve
is the wave and the orange dots are the microphone samplings.
This figure shows sampling for Fmic/F = {1, 2, 4, 8, 16}.
In the left panel the wave and samplings are depicted and in the right panel
only the samplings are depicted.
The top row corresponds to Fmic=F, and the wave cannot be detected at this sampling
frequency.
The second row corresponds to Fmic=2F, which is the Nyquist frequency. This frequency
is high enough to detect the wave but accuracy is poor.
For each successive row the value of Fmic/F is increased by a factor of 2.
The larger the value of Fmic/F, the more accurately the wave can be detected.
Human hearing has a frequency limit of 20000 Hertz, which corresponds to a Nyquist
frequency of 40000 Hertz. If you want to sample the highest frequencies accurately
then you need a frequency of at least 80000 Hertz.
Overtones can generate high-frequency content in a recording, which is why the
sampling frequency needs to be high.
The "spectrum" gives you the energy as a function of frequency.
The largest useful frequency F in the Fourier transform is the Nyquist
frequency.
The spectrum reveals the overtones of a pitch.
In the following plots the white curve is the waveform as a function of time
and the orange dots are the spectrum as a function of frequency.
The distorted sine wave gains overtones at higher frequencies. Distortion
always adds overtones.
The smooth structure has power at low frequencies and the rugged structure
has power at higher frequencies.
If the function is smooth then the Fourier transform can be a useful representation
of the function. If the function contains sharp jumps then the Fourier transform
fails.
Suppose a shock wave passes by, which is a sharp jump in pressure.
Such a wave looks like a "step function".
If you model a step function as a Fourier series the result is poor.
This is the "Gibbs phenomenon". No matter how many Fourier modes you use the
function always overshoots and oscillates.
A graphic equalizer allows you to amplify or suppress specific frequency
bands.
A Fourier transform can function like a graphic equalizer. For example, transform
the waveform A(T) to the C(F) and S(F) coefficients, change the coefficients according
to your taste, and then transform back to the waveform A(T).
Wikipedia:
Harmonic oscillator
Q factor
Resonance
Resonance
A force can stretch or compresses a spring.
A spring oscillates at a frequency determined by K and M.
Frequency = Squareroot(K/M) / (2 π)
For large q, the oscillations have a timescale of T and the damping
has a timescale of T*q. This can be used to measure the value of q.
If you shake a spring at the same frequency as the oscillation frequency
then a large amplitude can result. Similarly, a swing can gain a large
amplitude from small impulses if the impulses are timed with the swing period.
Suppose a violin A-string is tuned to 440 Hertz and a synthesizer produces a
frequency that is close to 440 Hertz. If the synthesizer is close enough to
440 Hertz then the A-string rings, and if the synthesizer is far from
440 Hertz then the string doesn't ring.
This is a plot of the strength of the resonance as a function of the
synthesizer frequency. The synthesizer frequency corresponds to the horizontal axis
and the violin string has a frequency of 440 Hertz. The vertical axis corresponds
to the strength of the vibration of the A-string.
A resonance has a characteristic width. The synthesizer frequency has to be
within this width to excite the resonance. In the above plot the width of the
resonance is around 3 Hertz.
Wind can make a string vibrate (The von Karman vortex).
The Tacoma Narrows bridge collapse was caused by wind exciting resonances in the
bridge.
The larger the value of q, the stronger the resonance.
The following plot shows resonance curves for various values of q.
If q>>1 then
You can break a wine glass by singing at the same pitch as the glass's
resonanant frequency. The more "ringy" the glass the stronger the resonance
and the easier it is to break.
The width of the resonance decreases with q. In the following plot the peak
amplitude of the resonance curve has been set equal to 1 for each curve.
As q increases the width of the resonance decreases.
The strings on an electric guitar are less damped than the strings on an acoustic
guitar. An acoustic guitar loses energy as it generates sound while an electric
guitar is designed to minimize damping. The resonances on an electric guitar are
stronger than for an acoustic guitar.
Oscillators that are mechanically connected can transfer energy back and forth
between them.
If you place your finger lightly on the string at the point of the green dot
then you can chose which mode appears.
If you pluck close to the bridge then overtones are favored.
You can change the frequency of the fundamental mode.
If you place two fingers on the string, one firmly at the left green dot and the
other lightly at the right green dot, then you can excite the 4th mode.
The left dot can be placed wherever you wish and then the position of the right
dot is fixed by the choice of overtone.
Resonances can be used to calibrate tuning. If you play a note on a violin then
it can excite resonances on the open strings. The pitch of the note is chosen
to maximize the resonances.
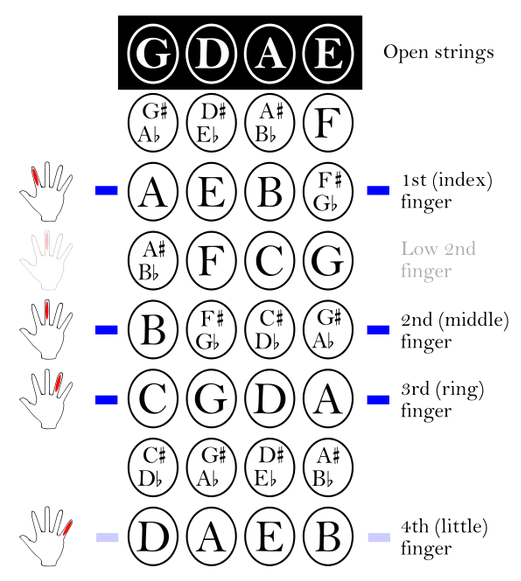
The strings on a violin, arranged from low to high frequency, are G, D, A, and E.
The notes on the strings are:
If you use your finger to play an "E" on the A-string it resonates with the
open E-string because both notes have the same frequency.
This is an example of a resonator and a driver. The open E-string is the
resonator because it has a fixed pitch and the E on the A-string is the driver
because its pitch can be changed by moving the finger. To calibrate your
tuning you can vary the position of your finger and listen for
the ring of the E-string and find the position that maximizes the ring.
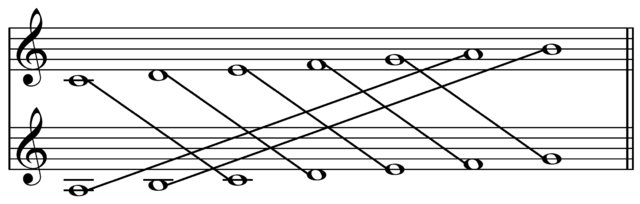
This figure lists some possibilities for resonance tuning, where
e ach set of 4 strings corresponds to one of the possibilities.
The first set corresponds to the above example and the 2nd and 3rd sets
are similar examples.
In the 4th set an A is played on the E string, which has twice the frequency of the
open A-string. The A on the E string resonates with the second mode on the open
A-string.
The 5th and 6th sets are similar examples.
In the 7th set an E is played on the D-string, and the second mode of this note
resonates with the open E string. The 8th set is a similar example.
The following table shows the notes on a violin, where notes that resonate with
open strings are colored in green.
The differential equation for a harmonic oscillator with damping is
If the string is forced by a driver with frequency f then the string vibrates
at this frequency. The amplitude for vibrations is
The width of the resonance occurs for a frequency f such that
Suppose you measure the frequency of a wave by counting the number of crests
and dividing by the time.
The equation for the uncertainty in a frequency measurement is
If two notes are played simultaneously then the pitches of the notes can be
calibrated by listening for beat frequencies.
This is also the precision limit for measuring relative frequencies using
just-intonation.
For low frequencies your ear is more precise than just-intonation.
For high requencies your ear is less precise than just-intonation.
The characteristic frequency for which the ear is equally precise as just-intonation
is F=170 Hertz.
If q is large then resonances are sharper than just-intonation. If q is small
then just-intonation is sharper than resonances.
A viola C-string has a frequency of 130 Hertz.
The lower the frequency of the note, the longer it takes to
sense its pitch.
The resonators in the ear have a characteristic quality parameter which can be
estimated from the frequency resolution of the ear.
If (T > Tres) then the ear resonators are fully activated.
When you start playing a note it takes a minimum of one wave period for the
tone to stabilize and it usualy takes longer. The lower the frequency of the
note the greater the challenge in starting the note quickly.
Summary of timescales:
Because the diameter of a whip tapers gradually, wave energy can be transmitted
from the handle to the tip. If the diameter were to change abruptly then wave
energy would be reflected at the transition, such as in the animation below.
The speed of a water wave slows down as it approaches shallow water, increasing the
wave amplitude.
A bow is tapered from the tip to the frog to prevent abrupt reflections of
wave energy. A tuba is flared at the end to smooth the transition from the
air inside the instrument to the air outside.
In a baseball pitch, the motion starts from the feet and then progresses to the
hips, the torso, the shoulder, the upper arm, the lower arm, the wrist, and then to
the fingers. This maximizes the speed that can be delivered by the fingers.
Sound energy does not transmit well between air and water because of the abrupt
change in density.
If someone is moving at 1 meter/second then the fractional change in frequency is
A harpshichord string is plucked and a piano string is hammered.
A harpsichord can't vary its volume.
The strings in a piano exert a force of 20 tons.
The Sydney Town Hall Grand Organ has pipes that are 64 feet long, which
corresponds to a frequency of 8.5 Hertz.
Amati (1505-1577) lived in Cremona, Italy, and developed the first violins, violas,
and cellos.
This violin, now at the Metropolitan Museum of Art, may have been part
of a set made for the marriage of Philip II of Spain to Elisabeth of Valois in
1559, which would make it one of the earliest known violins in existence.
Sound waves are fluctuations in air pressure. If there is silence then the air
pressure is constant in time. In the above figure a sound wave is passing by
and the listener perceives fluctuations in pressure.
Define a pressure fluctuation as follows:
The "Sound pressure level" is a logarithmic measure of the sound pressure.
Wikipedia: Sound pressure
Human hearing sensitivity depends on frequency. For example, a given sound pressure
is easier to hear at 1000 Hertz than at 10 Hertz.
Human perception of loudness is measured in "Phons", an emperical measure of
sensitivity obtained from experiments. The larger the value in Phons the louder the
sound seems.
The above figure relates the loudness in Phons to the pressure level Prms and frequency.
For example, a sound pressure of 100 decibels at a frequency of 20 Hertz has the same
loudness as a sound pressure of 40 decibels at a frequency of 1000 Hertz. Both
sounds have an apparent loudness of 40 Phons.
The lower the frequency the less sensitive our ears are. Elephants are sensitive
to extreme low frequencies. Human ears are unable to hear frequencies above
20000 Hertz.
Subwoofers are used to generate frequencies lower than 100 Hertz.
Because our ears are less sensitive to low frequencies the subwoofers are the
most critical element of a speaker system.
Wikipedia: Equal-loudness contours
The soundproofing effectiveness of a wall is proportional to the mass per area.
Example:
The lower the frequency, the harder it is to soundproof. In the example
we use the lowest frequency that a string bass or a bass guitar can
produce, which is 41 Hertz.
A soundproof wall should be able to attenuate sound by at least 40 decibells,
which corresponds to a sound transmission fraction of .01. We use this value in the example
and this yields a wall thickness of 161 kg/meter2.
The thickness of a wall depends on the density. For some common building materials, the
thickness that gives a mass/area of 161 kg/meter2 is:
Suppose a wall separates two rooms, an input room where sound is produced and an output
room where sound is received.
The formula works for (m>m0), otherwise almost all sound is transmitted through the wall.
For a wall to be effective in soundproofing it has to attenuate bass (F=F0) by at least 40 decibels (p2/p1 = .01), which corresponds to m = 161 kg/meter2.
If the subwoofer or amplifier produces distortion then overtones are produced.
Because our ears are insensitive to low frequencies, any distortion produced
becomes accentuated to our perception. Subwoofers and amplifiers tend to be the
most expensive elements in a speaker system.
The speaker system on the left has four speakers, each with a different frequency
band.
For example,
The energy in the moving air is
The power produced scales as frequency cubed and speaker size to the fifth power.
The density of water is 1000 greater than that for air, and so it is easier to produce
loud sounds underwater than in air.
For example, let
At high frequencies the maximum speaker power is determined by the quality of
the amplifier. At low frequencies the maximum speaker power is determined by
the size of the speakers.
As a wave propagates away from the speaker it diminishes in amplitude. The
right panel shows the amplitude as a function of distance for a spherical wave.
If you are in a small room then you can potentially generate more bass, if the
size of the room is less than the size of the wavelength. In this case, sound
can bounce back and forth between the walls and interfere constructively. If
the wavelength is less than the size of the room then the sound interferes
randomly, producing less amplification than constructive interference.
frequency of 40 Hertz corresponds to a wavelenght of 8.5 meters.
A rotary subwoofer uses a fan to move air, and the angle of the fan blades can
be changed to change the direction of the air. When it produces a sine wave it
alternately fans air back and forth. This design overcomes the low-frequency
limitation of diaphragm-based loudspeakers.
Trinity Church on Wall Street has a rotary subwoofer designed to simulate organ pipes
down to a frequency of 16 Hertz.
A microphone produces a voltage in the range of 1 to 100 microvolts.
A preamplifier amplifies this signal to the range of 10 volts, suitable for
recording by a computer. An "Audio interface" allows a computer to
interact with a set of microphones and speakers.
1) If a sound wave has a frequency of 40 Hertz and a speed of 340 meters/second,
what is the wavelength and wave period?
2) The strings on a violin, from low to high, are {G, D, A, E}.
If the A-string is tuned to 440 Hertz then what are the frequencies of
the other strings?
3) What is the frequency of a note that is 3 octaves above 440 Hertz?
4) A violin A-string has a length of .32 meters and a frequency of 440 Hertz.
What is the speed of the wave on the string?
5) Why doesn't a drum produce a well-defined pitch?
6) A pitch of 880 Hertz and 885 Hertz are played simultaneously. What is the beat
frequency?
Draw a sketch showing how two notes with nearly the same frequency can sum to
produce a beat frequency.
7) If a sound wave has a frequency of 880 Hertz, what is the Nyquist frequency
associated with this wave?
8) Draw a diagram of the ear illustrating each functional element (Ear bones,
cochlea, basilar membrane, etc). Describe how each element works, including
a discussion of the relevant physics.
9) Suppose a sound consists of two sine waves with the same amplitude.
One has a frequency of 1 and the other has a frequency of 3/2 (a fifth).
Draw the two sine waves and draw the waveform that is the sum of the two sines.
10) Sketch the first 3 overtones of a string.
Sketch the overtones of an oboe, assuming the oboe is an ideal open pipe.
If a string and a half-open pipe have a fundamental frequencies of 440 Hertz,
write down an expression for the frequencies of the overtones.
11) What are the notes in a D-major and D-minor scale on a treble clef?
12) Describe the history of tuning systems.
13) What is the frequency of a note that is 1/10 of a half step above 880 Hertz?
(use equal tuning).
14) Describe an experiment for measuring the width of the resonance of a string.
15) A guitar A-string has a length of .65 meters and the frets are set by equal
tuning. The frets are ordered {A, Bflat, B, C, C#, D, Eflat, E, etc}. What is
the distance between the D and E frets?
17) Draw a set of diagrams showing how two waves traveling in opposite directions can
sum to form a standing wave.
18) What is the frequency ratio of a perfect fourth, using just-intonation and
equal-temperament?
19) What is the relative major of D-minor?
20) Describe a strategy for breaking a wineglass by singing.
21) Describe a strategy for soundproofing a room.
22) Draw a diagram illustrating the loudness sensitivity of the ear as a function of
frequency.
23) Draw a diagram illustrating how noise-canceling headphones work.
24) What is the definition of a diatonic mode? (what properties must it have)
25) Sketch a typical spectrum for a stringed instrument where all overtones are
present.
26) If you increase the radius of a string by a factor of 2 what happens to its
frequency?
27) For the wind and brass instruments, use the instrument length to estimate
the frequency of the lowest possible note and compare it to the actual lowest
frequency.
28) If a violin G string has a tension of 50 Newtons and a density of 8 g/cm^3,
what is the diameter?
1) If a sound wave has a frequency of 40 Hertz and a speed of 340 meters/second,
what is the wavelength and wave period?
Wavelength = 340 / 40 = 8.5 meters
Period = 1/40 = .025 seconds
2) The strings on a violin, from low to high, are {G, D, A, E}.
If the A-string is tuned to 440 Hertz then what are the frequencies of
the other strings?
3) What is the frequency of a note that is 3 octaves above 440 Hertz?
Frequency = 440 * 2 * 2 * 2 = 3520 Hertz
4) A violin A-string has a length of .32 meters and a frequency of 440 Hertz.
What is the speed of the wave on the string?
Speed = 2 * Length * Frequency = 282 meters/second
5) Why doesn't a drum produce a well-defined pitch?
The overtone frequencies are not integer ratios of the fundamental frequency.
6) A pitch of 880 Hertz and 885 Hertz are played simultaneously. What is the beat
frequency?
Draw a sketch showing how two notes with nearly the same frequency can sum to
produce a beat frequency.
Beat frequency = 885 - 880 = 5 Hertz
7) If a sound wave has a frequency of 880 Hertz, what is the Nyquist frequency
associated with this wave?
Nyquist frequency = 880 * 2 = 1760 Hertz
8) Draw a diagram of the ear illustrating each functional element (Ear bones,
cochlea, basilar membrane, etc). Describe how each element works, including
a discussion of the relevant physics.
9) Suppose a sound consists of two sine waves with the same amplitude.
One has a frequency of 1 and the other has a frequency of 3/2 (a fifth).
Draw the two sine waves and draw the waveform that is the sum of the two sines.
10) Sketch the first 3 overtones of a string.
Sketch the overtones of an oboe, assuming the oboe is an ideal open pipe.
If a string and a half-open pipe have a fundamental frequencies of 440 Hertz,
write down an expression for the frequencies of the overtones.
11) What are the notes in a D-major and D-minor scale on a treble clef?
12) Describe the history of tuning systems.
13) What is the frequency of a note that is 1/10 of a half step above 880 Hertz?
(use equal tuning).
Frequency = 880 * 2^(1/120) = 885 Hertz
14) Describe an experiment for measuring the width of the resonance of a string.
15) A guitar A-string has a length of .65 meters and the frets are set by equal
tuning. The frets are ordered {A, Bflat, B, C, C#, D, Eflat, E, etc}. What is
the distance between the D and E frets?
16) Draw a diagram showing how the resonance curve behaves as a function of
the quality parameter.
17) Draw a set of diagrams showing how two waves traveling in opposite directions can
sum to form a standing wave.
18) What is the frequency ratio of a perfect fourth, using just-intonation and
equal-temperament?
Just-intonation = 4/3 = 1.3333
Equal-temperament = 2^(5/12) = 1.335
19) What is the relative major of D-minor?
F-major. The relative major is 3 half steps above the relative minor.
20) Describe a strategy for breaking a wineglass by singing.
Identify the glass that rings the longest. Sing pitches until you find the pitch
that makes the glass shake and then maximize the volume at that pitch.
21) Describe a strategy for soundproofing a room.
Multi-layered walls and windows with lots of mass.
Carpets and sofas and bookshelves.
In an anechoic chamber, the walls are made out of cones designed to not reflect
sound back into the room.
22) Draw a diagram illustrating the loudness sensitivity of the ear as a function of
frequency.
23) Draw a diagram illustrating how noise-canceling headphones work.
24) What is the definition of a diatonic mode? (what properties must it have)
25) Sketch a typical spectrum for a stringed instrument where all overtones are
present.
26) If you increase the radius of a string by a factor of 2 what happens to its
frequency?
WaveSpeed^2 = Tension / (Density * Pi * Radius^2)
Frequency = WaveSpeed / (2 * Length)
Doubling the radius halves the frequency.
Conduct an experiment to measure the sensitivity of human frequency perception.
For example, suppose you use a sound generator to produce a frequency of 440
Hertz and then slowly change the frequency until you notice that the frequency
has changed.
You can also use an instrument to produce the frequencies.
Suppose a violin string is tuned to 440 Hertz and a synthesizer produces a
frequency that is close to 440 Hertz.
You can use any instrument as a source of resonances.
Notes on damping and resonance
As an example, run the
resonance
simulation at phet.colorado.edu, where you can vary the synthesizer frequency
and observe the amplitude of the resonance. The resonator has a resonant
frequency of 1.0 Hertz and the width of the resonance is .1 Hertz.
Obtain a power spectrum app for your phone and experiment with speaker systems.
How accurately do the speakers reproduce overtones when played at large volume,
and how does the behaviour depend on frequency?
For a subwoofer, what do you measure for the lowest-frequency sound that it can
produce without your ear sensing distortion? Draw diagrams showing the
distortion and the overtones. Describe the speaker system.
Let Theta be the characteristic angle for which you can sense the direction of
a sound. Conduct a set of experiments to measure Theta as a function of frequency.
What are the results for pure sine waves and for signals with abundant overtones?
What is the effect of noise?
Find a set of youtube videos on some aspect of motion (playing an instrument, singing,
speaking, dancing, sports, etc.) and analyze the physics.
Build a musical instrument.
Build an anechoic chamber.
For a set of instruments, measure the loudness as a function of frequency.
Perform a piece of chamber music for the class with a small ensemble.
Write a pop-science article relevant to this class.
Find web resources, figures, and animations that are useful for this class.
Contribute to a wikipedia article relevant to this course.
If there is a pop-science article on the web that is flawed, write an article
exposing the flaws.
Build an extreme subwoofer.
Sound in the animal kingdom.
Experiment with audio compression software and study the effect of compression
options on the ear. How does the quality of the speaker system affect the result?
Do hearing experiments in the presence of minimal noise.
Optical and aural illusions.
Find youtube videos involving motion, such as playing an instrument, singing,
speaking, dance, sports, etc., and analyze the physics.
Find an App that functions as a musical instrument and explore its possibilities.
Write an App that functions as a musical instrument.
Noise pollution, both on land and in the ocean.
Develop computer-synthesized sounds.
Use a audio analysis software to analyze sound.
Describe exotic instruments or tuning systems.
Design an interesting homework or exam problem.

1523 Pietro Anon introduced "meantone tuning" to fix the thirds, using a
frequency ratio of 5/4 for major thirds. His treatise "Thoscanello de la
musica" expanded the possibilities for chords and harmony.
1555 Amati develops the 4-string violin
1584 Equal tuning developed. Equal tuning divides the octave logarithmically.
The first known examples were:
Vincenzo Galilei in 1584 (Father of Galileo Galilei)
Zhu Zaiyu in 1584
Simon Stevin in 1585
1585 Simon Stevin introduces decimal numbers to Europe.
(For example, writing 1/8 as 0.125)
1586 Simon Stevin drops objects of varying mass from a church tower to demonstrate that
they accelerate uniformly.
1604 Galileo publishes a mathematical description of acceleration.
1614 Logarithms invented by John Napier, making possible precise calculations
of equal tuning ratios. Stevin's calculations were mathematically sound but
the frequencies couldn't be calculated with precision until logarithms were
developed.
1637 Cartesian geometry published by Fermat and Descartes.
This was the crucial development that triggered an explosion of mathematics
and opened the way for the calculus.
1672 Newton builds the first reflecting telescope and presents it to the Royal Society

1684 Leibniz publishes the calculus
1687 Newton publishes the Principia Mathematica, which contained the calculus,
the laws of motion (F=MA), and a proof that planets orbit as ellipses.
1722 Bach publishes "The Well Tempered Clavier".
Until ~ 1650, most keyboards used meantone tuning. This tuning gives good
results if you confine yourself to a small number of keys and use few
accidentals, but it can't be made to work for all keys.

1733 Euler develops the calculus of variations
1762 Lagrange discovers the divergence theorem, the 2D generalization of the
fundamental theorem of calculus.
The surface flux integral equals the volume divergence integral
1788 Lagrangian mechanics published
1821 Cauchy publishes the "epsilon-delta" definition of a limit, raising the
level of rigor in mathematics.
1822 Fourier transform published
1828 Green's theorem. In 2D, the circulation integral equals the curl area integral
1833 Hamiltonian mechanics published
1834 Eikonal approximation developed by Hamilton
1850 Kelvin-Stokes theorem. 3D generalization of Green's theorem
1854 Riemann Integral published, the first rigorous definition of an integral
1854 Chebyshev polynomials published
1863 Helmholtz publishes "On the Sensations of Tone"
1870 Heine defines "uniform continuity"
1872 Heine proves that a continuous function on an open interval need not be
uniformly continuous.
1872 Weierstrass publishes the "Weierstrass function", the first example of
a function that is continuous everywhere and differentiable nowhere.
1877 Lord Rayleigh publishes "Theory of Sound"
1887 Poincare discovers the phenomenon of chaos while studying celestial mechanics
1926 WKB theory published
1935 Bourbaki textbooks published, with the aim of reformulating mathematics on
an extremely abstract and formal but self-contained basis. With the goal
of grounding all of mathematics on set theory, the authors strove for rigour
and generality.
1978 "Bender & Orszag" textbook published. Art of blending special functions
like Scotch.

R = (3/2) / (4/3) = 9/8 = 1.125
In a 12-tone equal-tempered scale the frequency ratio of a whole step is
R = 2(2/12) = 1.122
which is nearly the same as the ratio between a fourth and a fifth.
This is why the 12-tone scale works so well. If you try any number other than
12 it doesn't work. This is why the 12-tone scale is the most useful
for writing harmony.
Interval Frequency ratio Cents
0 cents 20/12 = 1 0
1 cent 21/1200= 1.0006 1
10 cents 21/120 = 1.0058 10
Half step 21/12 = 1.0595 100
Whole step 22/12 = 1.1225 200
Fifth 27/12 = 1.498 700
Octave 212/12 = 2 1200
I = Note index, where I=1 is a half step, I=2 is a whole step, and I=12 is an octave
C = Cents
= I/100
F = Frequency ratio
= 2I/12
= 2C/1200
C = 1200 ln(F) / ln(2)
If F has the form
F = 1 + Z where Z << 1
then
C = 1200 ln(1+Z) / ln(2)
~ 1200 Z / ln(2)
~ 1731 Z
For example, the frequencies for a fifth are
Equal tuning: Fe = 27/12 = 1.4983
Just tuning: Fj = 3/2 = 1.5000
These frequencies have the ratio
F = Fj / Fe
= 1.00113
Z = F - 1
= .00113
C = 2.0
The frequencies for just and equal tuning differ by 2 cents.
21/12 = 1.059
Human are capable of detecting a change in frequency of 1/10 of a half step,
which corresponds to a frequency ratio of
21/120 = 1.0056
To appreciate a 12-tone scale one must have precision that is tangibly smaller
than a half step. Humans are well within this bound.
I = Index of a note. I=0 for the tonic and I=12 for the octave
F = Frequency of a note on the A-string
= 440 * 2I/12
f = Smallest frequency greater than 440 Hertz for which "f" sounds
indistinguishable
from "F"
~ 443 Hertz
R = Characteristic frequency ratio for human sensitivity
= f / F
~ 1.0058
1-R = .0058 = 1/173
Note I F
A 0 440 Open A-string
.1 442.5 Largest frequency that sounds indistinguishable from 440 Hertz
Bb 1 466 Half step
B 2 494 Whole step
C 3 523
C# 4 554
D 5 587 Perfect fourth
Eb 6 622 Tritone
E 7 659 Perfect fifth
F 8 698
F# 9 740
G 10 784
G# 11 831
A 12 880 Octave
Note I F
A 0 880
.1 885 Largest frequency that sounds indistinguishable from 880 Hertz
Bb 1 932 Half step
B 2 988 Whole step
...



















String Baroque Modern
quartet orchestra orchestra
First violin 1 4 16
Second violin 1 4 14
Viola 1 4 12
Cello 1 4 12
Bass 2 8
Flute 2 4
Oboe 2 4
Clarinet 4
Bassoon 2 4
Trumpet 2 4
French Horn 2 4
Trombone 4
Tuba 2
Harpsichord 1
Timpani 1 1
Hertz
Violin E 660 = 440*1.5
Violin A 440
Violin D 293 = 440/1.5
Violin G 196 = 440/1.52
Viola A 440 Same as a violin A
Viola D 293
Viola G 196
Viola C 130
Cello A 220 One octave below a viola A
Cello D 147
Cello G 98
Cello C 65
String bass G 98 = 55 * 1.52
String bass D 73 = 55 * 1.5
String bass A 55 3 octaves below a violin A
String bass E 41 = 55 / 1.5
Guitar E 326
Guitar B 244
Guitar G 196
Guitar D 147
Guitar A 110 2 octaves below a violin A
Guitar E 82
When an orchestra tunes, the concertmaster plays an A and then everyone tunes
their A strings. Then the other strings are tuned in fifths starting from the A.
Strings Winds Brass Voice
D Piccolo
C Flute Soprano
Bb Oboe
A
G Violin
F# Trumpet Alto
E Guitar Clarinet
D
C Viola Tenor
Bb
A
G Baritone
F# Horn
E Trombone Bass
D
C Cello
Bb Bassoon
A
G
F
E Bass
D Tuba
Treble clef: Violin, flute, oboe, clarinet, saxophone, trumpet, French horn, guitar,
soprano voice, alto voice, tenor voice.
Alto clef: Viola
Base clef: Cello, bass, bass guitar, bassoon, trombone, tuba, timpani,
baritone voice, bass voice
String basses and bass guitars have the same string tuning.





















L = Length of an open A-string
= .65 meters
T = Wave period
F = Frequency of the A-string
= 220 Hertz
V = Speed of a wave on the A-string
= 2 L F
= 2 * .65 * 220
= 286 meters/second
I = Index of a fret
= 1 for B flat
= 2 for B
= 3 for C, etc.
f = Frequency of note I
= F * 2^(I/12)
X = Distance from the bridge to fret I
= V / (2 f)
= V / (2 F) * 2^(-I/12)
= L * 2^(-I/12)
I Note X L-X
0 A .650 .0
1 Bb .614 .036
2 B .579 .071
3 C .547 .103
4 C# .516 .134
5 D .487 .163
6 Eb .460 .190
7 E .434 .216
8 F .409 .241
9 F# .386 .264
10 G .365 .285
11 Ab .344 .306
12 A .325 .325
G = 1
D = 3/2
A = 9/4
The G-string has been normalized to have a frequency of 1. There are several
possibilities for assigning the pitch of the "E" on the D-string.
E = 5/3 = 1.6666
If the note "E" is chosen to resonate with the "A-string" then it is placed
a perfect fourth below the A.
E = (9/4) / (4/3) = 27/16 = 1.688
If the note "E" is played with equal tuning with the G-string as the tonic,
E = 2^(9/12) = 1.682
All three values for the E are different. Musicians have to develop a sensitivity
for this.

Red: Equal tuning
Green: Just tuning
Orange: Pythagorean tuning
Indian music has two separate tones for each half step, one from just tuning and
the other from Pythagorean tuning. For the tonic and the fifth these
tones are the same for both tunings. There are 22 tones in total.

A Octave
G
F
E Perfect fifth
D Perfect fourth
C
B
A Tonic
There is a half step between the B and C and another half step between the E and
F. All other intervals are whole steps.
* oo o oo o * oo o oo o * oo o oo o * oo o oo o * (Minor scale)
A BC D EF G A BC D EF G A BC D EF G A BC D EF G A
A "*" indicates the tonic and an "o" denotes a note in the scale.
Each successive "*" denotes an octave. Four octaves are depicted.
Each half step is at least 2 whole steps from another half step.
There are no gaps larger than a whole step.
There are 8 notes spanning the octave.
* o oo o o o* o oo o o o* o oo o o o* o oo o o o* (4 octaves of a major scale)
A B CD E F GA
# # #
In an A-minor scale there are no flats or sharps. In an A-major scale
the sharped notes are C#, F#, and G#.
(*) The tonic and octave are both included
(*) There are 8 notes including the tonic and octave
(*) Steps larger than a whole step are forbidden
(*) There must be at least 2 whole steps separating each half step,
including octave periodicity
The scale has 2 half steps and 5 whole steps.
The half steps are separated by 2 whole steps in one direction and 3 whole steps
in the other direction.
There is exactly 1 tritone.
There are 7 modes that satisfy the definition.
o o oo o o oo o oo o o oo o oo o o oo
There are 7 unique choices of tonic which correspond to the 7 diatonic modes.
o o oo o o oo o oo o o oo o oo o o oo
I D PL M A lI
I = Ionian
D = Dorian
P = Phrygian
L = Lydian
M = Mixolydian
A = Aeolian
l = Locrian
I = Ionian
The tritone defines a natural sequence for the modes that we'll call the
"Diatonic sequence". When the modes are arranged this way, adjacent modes differ
by exactly one pitch and distant modes can be continuously connected by the
tritone sequence.
Inverted Lydian = Locrian
Inverted Ionian = Phrygian
Inverted Mixolydian = Aeolean
If an instrument is tuned in fifths there is a symmetry between modes and strings.
Transposing up one string corresponds to transposing up one mode and transposing
down one string corresponds to transposing down one mode.
o o o oo oo o o o oo oo o o o oo oo o o o oo oo o
Notes Mode Sharpness
o o o oo o oo Lydian 3
o o oo o o oo Ionian 2 Major mode
o o oo o oo o Mixolydian 1
o oo o o oo o Dorian 0
o oo o oo o o Aeolian -1 Minor mode
oo o o oo o o Phrygian -2
oo o oo o o o Locrian -3
o o o o oo oo Lydian sharp 5 4
o o o oo oo o Lydian/Mixolydian 2
o oo o o o oo Melodic minor 1
o o oo oo o o Mixolydian/Aeolian 0
oo o o o oo o Dorian/Phrygian -1
o oo oo o o o Aeolian/Locrian -2
oo oo o o o o Locrian flat 4 -4
Sharpness = Sum over all notes of (I - 6)
If you start with a diatonic mode and move one of the tritone pitches by
a half step then you get an adjacent diatonic mode. If you change
a non-tritone pitch by a half step then you get a melodic mode.
The keys of A-minor and C-major share the same notes. A-minor is the "relative minor"
of C-major and C-major is the "relative major" of A-minor. These two keys also have
no sharps or flats.
A
D
G
C
F
B flat
E flat
A flat
C#
F#
B
E
A
A-minor (same notes as C-major)
G-major
E-minor (same notes as G-major)
D-major
B-minor (same notes as D-major)
etc.
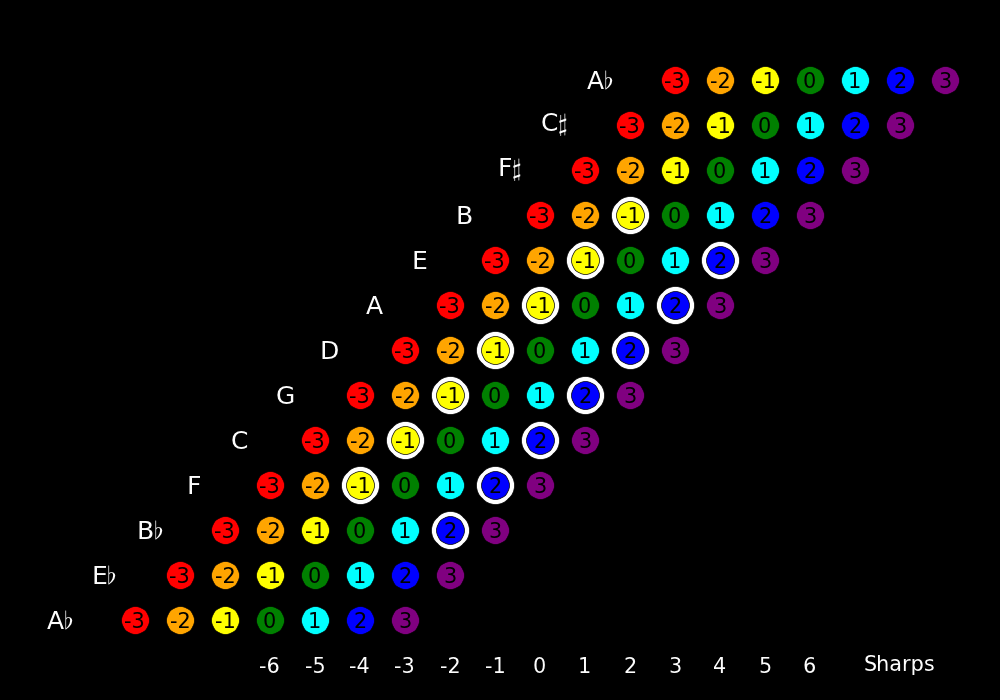
The most commonly used keys are indicated by dots with white edges.
They tend to cluster vertically around the strings of a violin because they are
the most convenient for a violin to play. This forms a sweet spot in the
circle of fifths.
G-minor
B-minor
A-minor
D-minor
C-major
E-major
D-major (occurs twice)
D-minor
G-minor
G-major
E-minor
E-major
A-minor (occurs twice)
A-major
F-major
B-minor


Two surfaces are topologically equivalent if they can be connected by a continuous
deformation. For example, a coffee mug is topologically equivalent to a torus.








Define "gap size" as being 1 for a half step, 2 for a whole step, etc.
oo oo o oo o
oo oo oo o o
oo oo o oo o
oo oo oo o o
oo o oo oo o
Each sequences has 3 doublets and 2 tritones and each is asymmetric.
ooo oo o o o
There are 7 choices of tonic and so this sequence generates 7 scales. It is
asymmetric and so its inversion also generates 7 scales.
The inversion: o o o oo ooo
The Indian raga contain all the diatonic and melodic modes except the Locrian and
Locrian-flat-4 modes, the modes with the most flats.


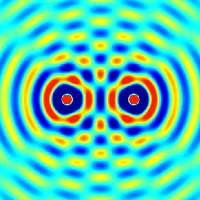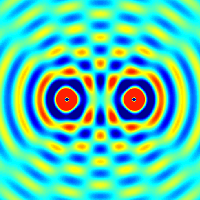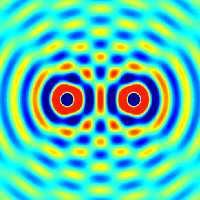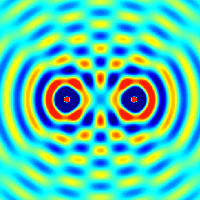
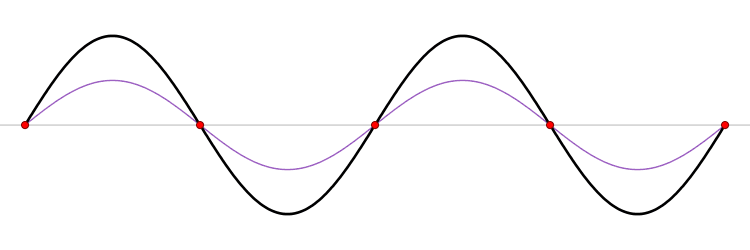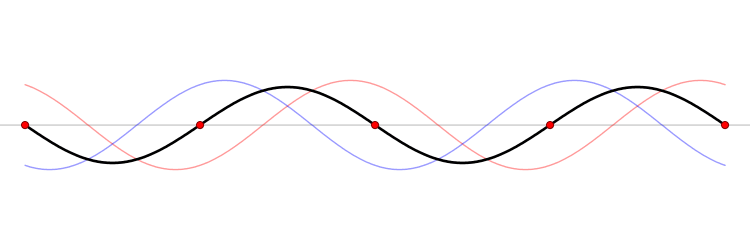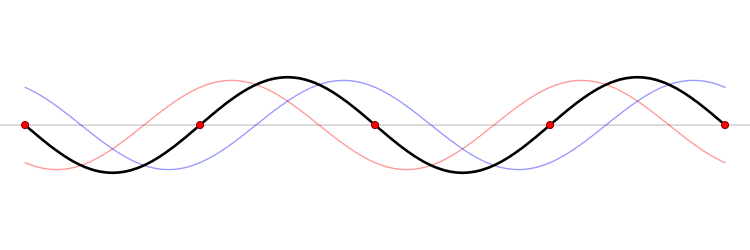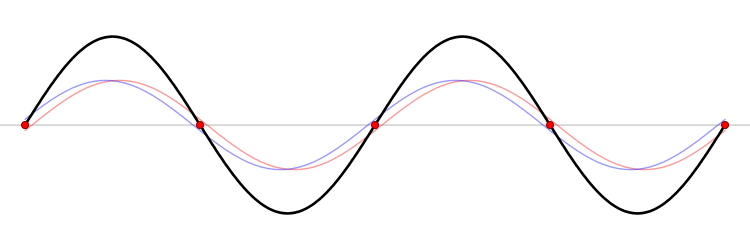

Whan a wave on a string encounters an endpoint it reflects with the waveform
preserved and the amplitude reversed.
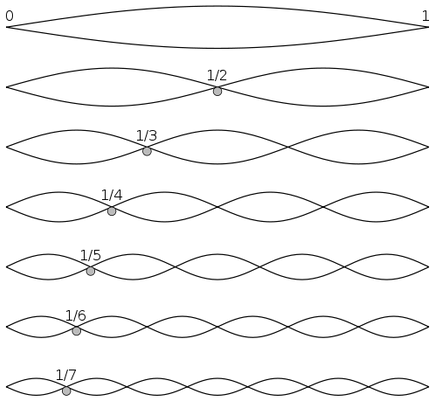

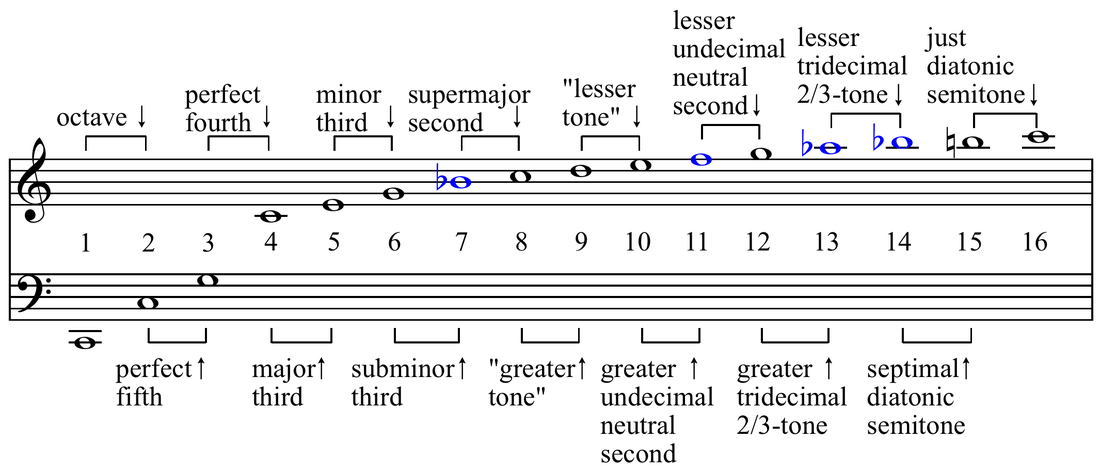
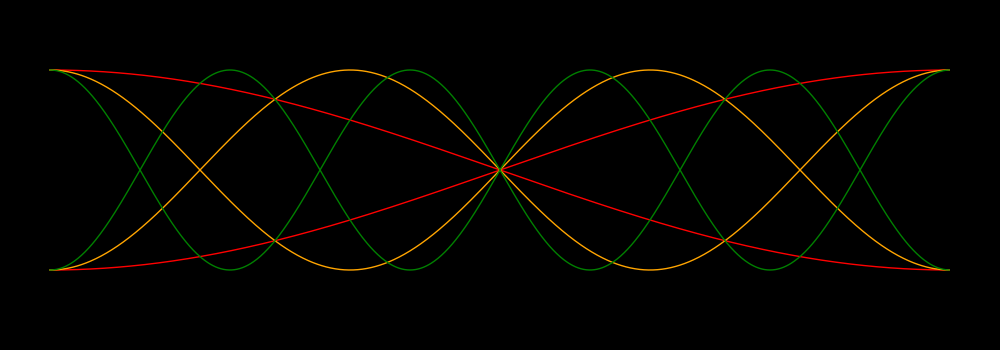
When an string is played it creates a set of standing waves.
L = Length of a string
V = Speed of a wave on the string
N = An integer in the set {1, 2, 3, 4, ...}
W = Wavelength of an overtone
= 2 L / N
F = Frequency of the overtone
= V/W
= V N / (2L)
N = 1 corresponds to the fundamental tone
N = 2 is one octave above the fundamental
N = 3 is one octave plus one fifth above the fundamental.
Audio: overtones
Overtone Frequency Note
1 440 A
2 880 A
3 1320 E
4 1760 A
5 2200 C#
6 2640 E
7 3080 G
8 3520 A
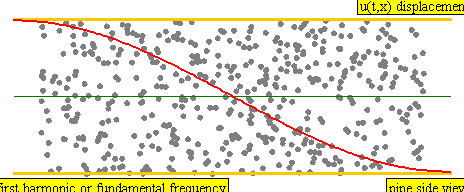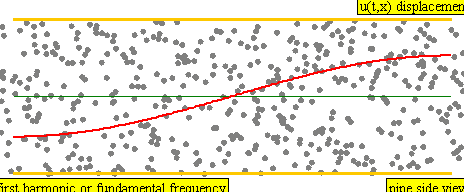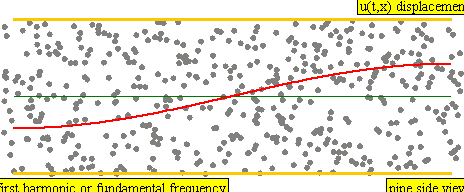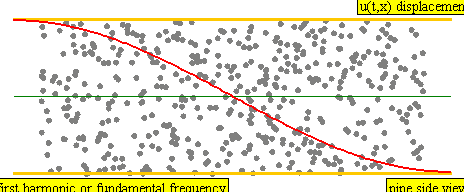
In the left frame the pipe is open at the left and closed at the right.
In the right frame the pipe is reversed, with the left end closed and the right
end open. Both are "half-open pipes".
L = Length of the pipe
~ .6 meters for an oboe
V = Speed of sound
N = An odd integer having values of {1, 3, 5, 7, ...}
W = Wavelength of the overtone
= 4 L / N
F = Frequency of the overtone
= V / W
= V N / (4L)
The overtones have
N = {1, 3, 5, 7, etc}
L = Length of the pipe
V = Speed of sound
N = An odd integer having values of {1, 3, 5, 7, ...}
W = Wavelength of the overtone
= 2 L / N
F = Frequency of the overtone
= V / W
= V N / (2L)
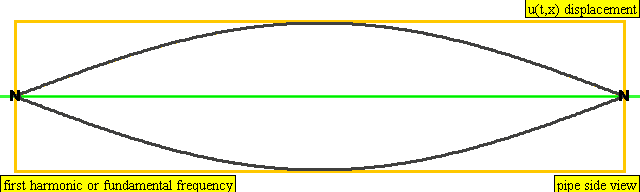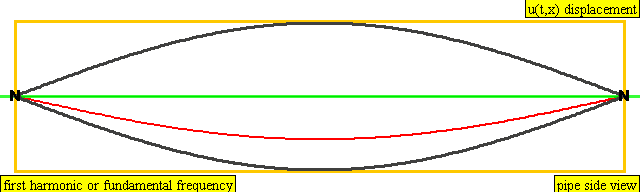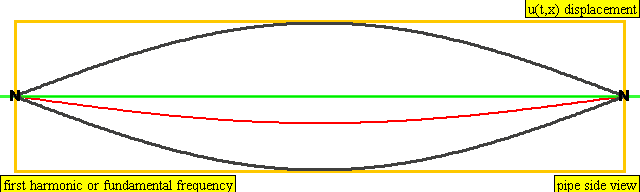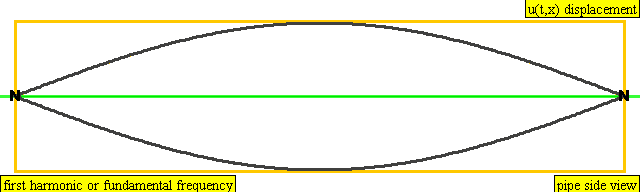
A string has the same overtones as a closed pipe.
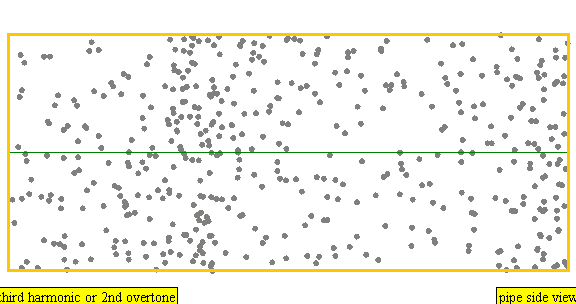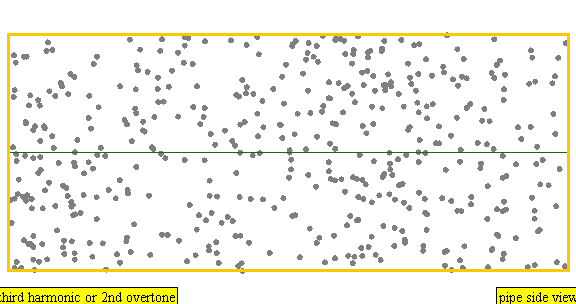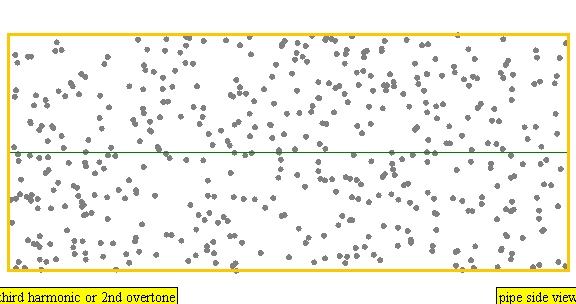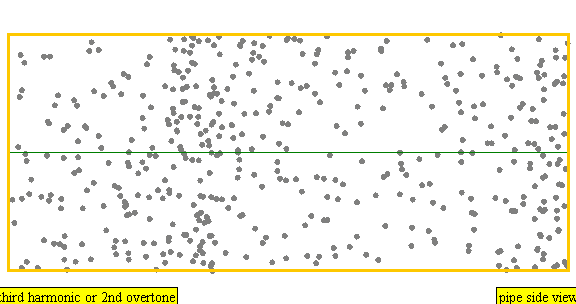
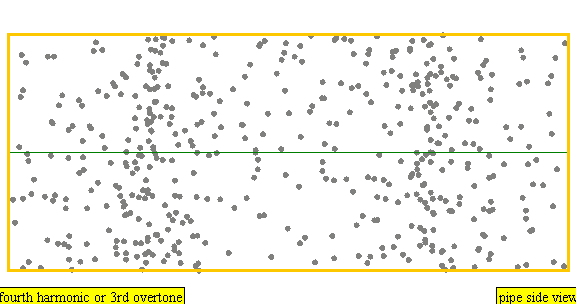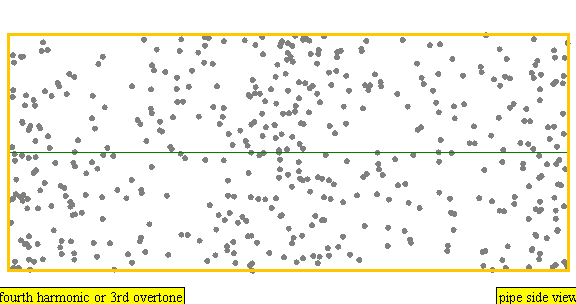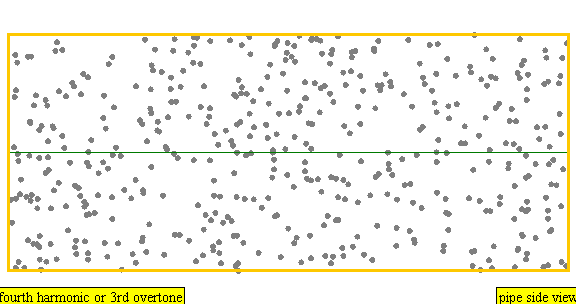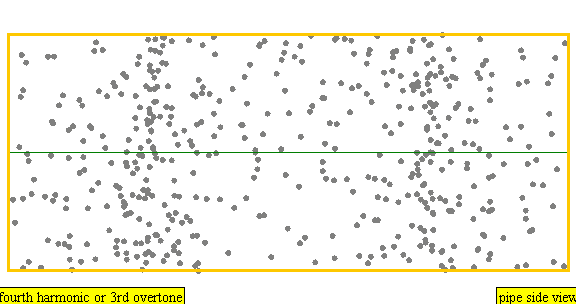
An instrument of length L has overtones with frequency
Frequency = Z * Wavespeed / (2 * Length)
Z corresponds to the white numbers in the figure above.
Violin 440, 2*440, 3*440, 4*440, ...
Oboe 440, 3*440, 5*440, 7*440, ...
Flute 440, 3*440, 5*440, 7*440, ...
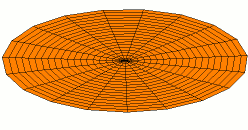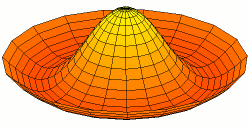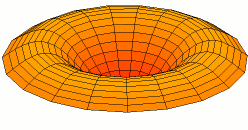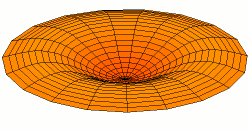
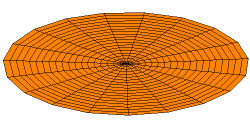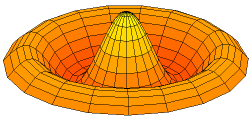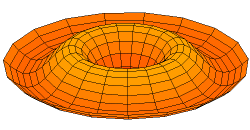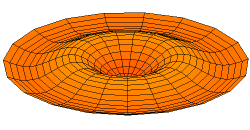
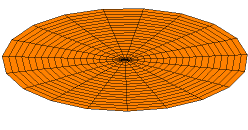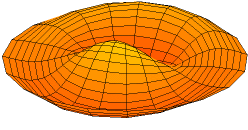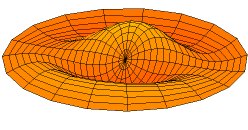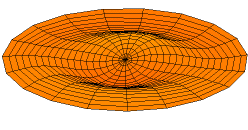
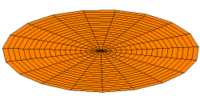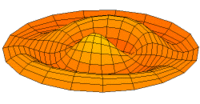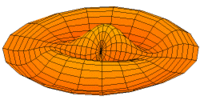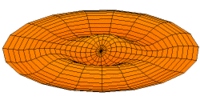
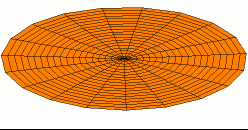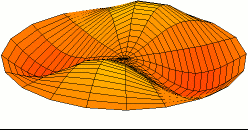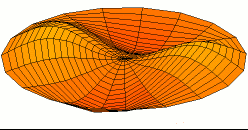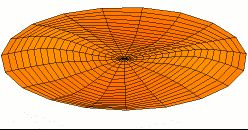


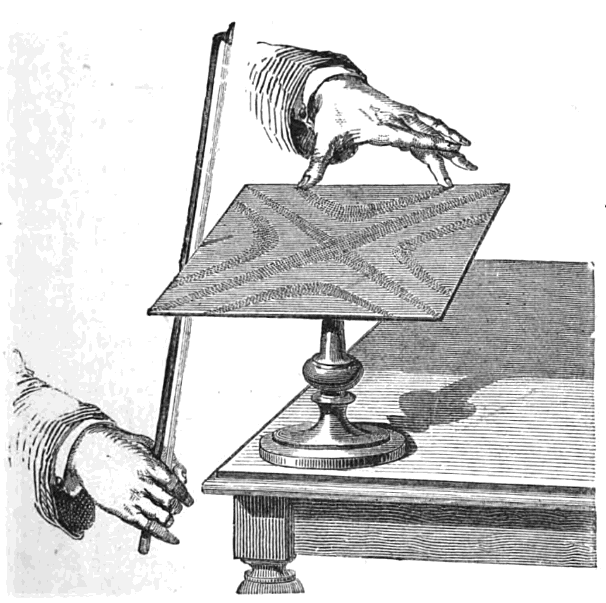
In 1787 Chladni published observations of resonances of vibrating plates.
He used a violin bow to generate a frequency tuned to a resonance of the plate
and the sand collects wherever the vibration amplitude is zero.


L = Length of string
N = An integer greater than or equal to 1
X = Position along the string
H = Height of the standing wave as a function of X
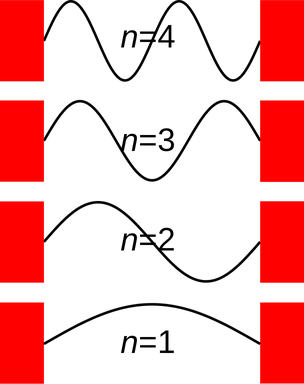
H = sin(π N X / L)
L = Side length of the cube
Nx = An integer >= 1 representing the mode number in the X direction
Ny = An integer >= 1 representing the mode number in the Y direction
Nz = An integer >= 1 representing the mode number in the Z direction
N = SquareRoot(Nx2 + Ny2 + Nz2)
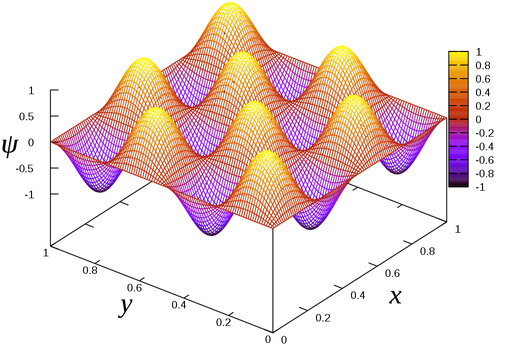
H = Height of the standing wave as a function of X, Y, and Z
V = Wave velocity
W = Wavelength of mode (Nx,Ny,Nz)
H = sin(π Nx X / L) * sin(π Ny Y / L) * sin(π Nz Z / L)
The frequency of a mode {Nx, Ny, Nz} is proportional to N.
F = N V / (2L)
For simplicity we set V/(2L) = 1 so that
F = N = SquareRoot(Nx2 + Ny2 + Nz2)
For example, the modes of a 1D string are
Nx N
1 1
2 2
3 3
4 4
... ...
The modes of a 2D square are
Nx Ny N
1 1 SquareRoot( 2) = 1.41
1 2 SquareRoot( 5) = 2.24
2 1 SquareRoot( 5) = 2.24
2 2 SquareRoot( 8) = 2.83
1 3 SquareRoot(10) = 3.16
3 1 SquareRoot(10) = 3.16
2 3 SquareRoot(13) = 3.61
3 2 SquareRoot(13) = 3.61
1 4 SquareRoot(17) = 4.12
4 1 SquareRoot(17) = 4.12
3 3 SquareRoot(18) = 4.24
2 4 SquareRoot(20) = 4.47
4 2 SquareRoot(20) = 4.47
... ... ...
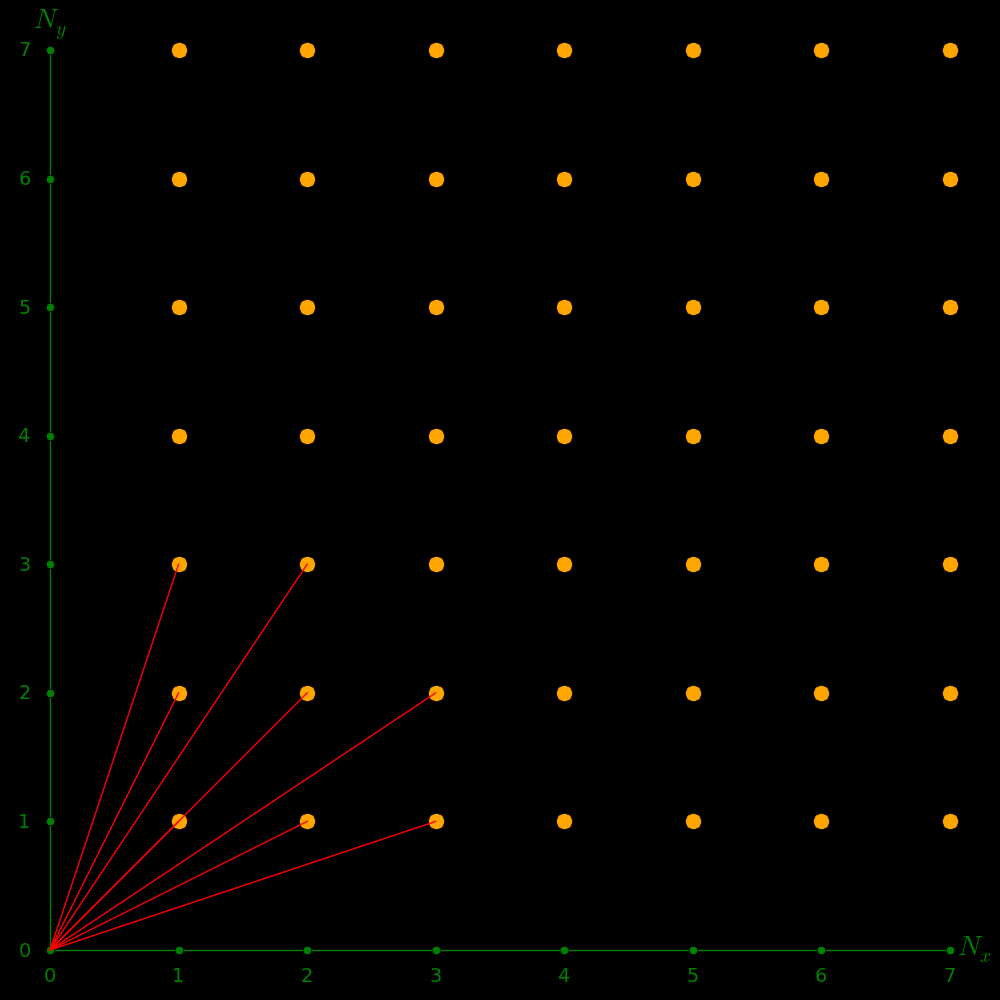
Nx Ny Nz N
1 1 1 SquareRoot( 3) = 1.41
1 1 2 SquareRoot( 6) = 2.45
1 2 1 SquareRoot( 6) = 2.45
2 1 1 SquareRoot( 6) = 2.45
1 2 2 SquareRoot( 9) = 3.00
2 1 2 SquareRoot( 9) = 3.00
2 2 1 SquareRoot( 9) = 3.00
1 1 3 SquareRoot(11) = 3.32
1 3 1 SquareRoot(11) = 3.32
3 1 1 SquareRoot(11) = 3.32
2 2 2 SquareRoot(12) = 3.46
1 2 3 SquareRoot(14) = 3.74
1 3 2 SquareRoot(14) = 3.74
2 1 3 SquareRoot(14) = 3.74
2 3 1 SquareRoot(14) = 3.74
3 1 2 SquareRoot(14) = 3.74
3 2 1 SquareRoot(14) = 3.74
... ... ... ...
Dimension Number of mode with N < M
1 M
2 (1/4) π M2
3 (1/8) (4π/3) M3
In 2D the number 1/4 represents a quadrant of the plane an in 3D the number 1/8
represents an octant of a volume.
Z = Membrane tension in Newtons/meter = 2000 Newtons/meter for a typical typani
M = Membrane density in kg/meter2 = .26 kg/meter2 for a typical tympani
D = Membrane diameter = .6 meters for a typical tympani
F = Fundamental mode frequency = 112 Hertz for a typical tympani
= .766 SquareRoot(Z/(MD))
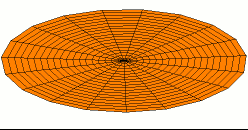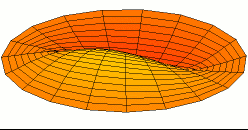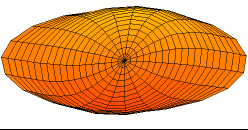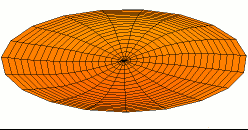
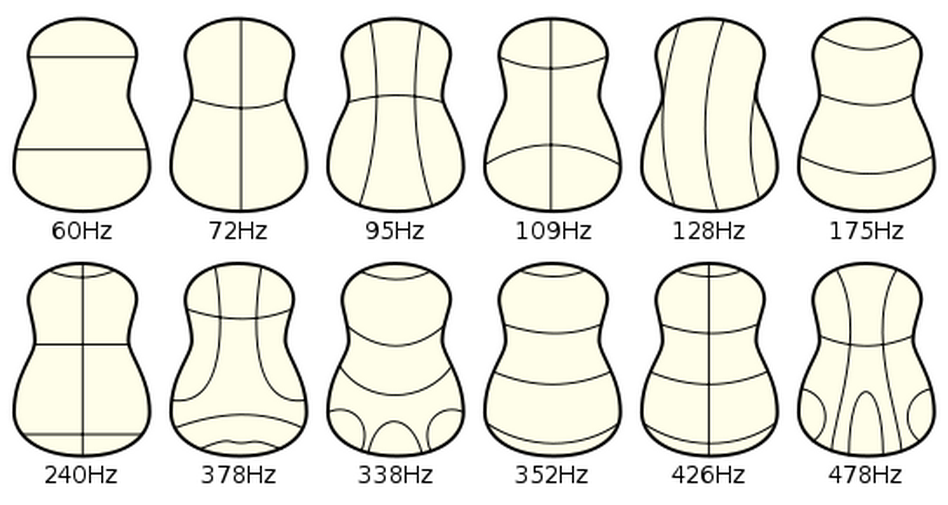
Drum modes in order of increasing frequency are
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
>>> from scipy.special import jn_zeros # Compute the zeros of the Bessel function
>>> jn_zeros(0,4)/jn_zeros(0,1) # Compute the first 4 monopole modes
>>> jn_zeros(1,4)/jn_zeros(0,1) # Compute the first 4 dipole modes
>>> jn_zeros(2,4)/jn_zeros(0,1) # Compute the first 4 quadrupole modes




The interior of a football is a spherical resonator.



Tension = Tension of a string
D = Mass per meter of the string
V = Speed of a wave on the string
= (Tension/D)½
L = Length of the string
T = Wave period of a string (seconds)
= 2 L / V
F = Frequency of a string
= 1/T
= V / (2L)


As a sound waves travels back and forth along an oboe it forces the reed to
vibrate with the same frequency.
In the figure, as the flow constricts it speeds up and drops in pressure.
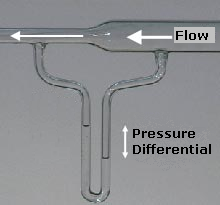
P = Pressure
V = Fluid velocity
H = Height
g = Gravity = 9.8 meters/second2
D = Fluid density
The bernoulli principle was published in 1738. For a steady flow, the value of "B"
is constant along the flow.
B = P + .5 D V2 + D g H
If the flow speeds up the pressure goes down and vice versa.
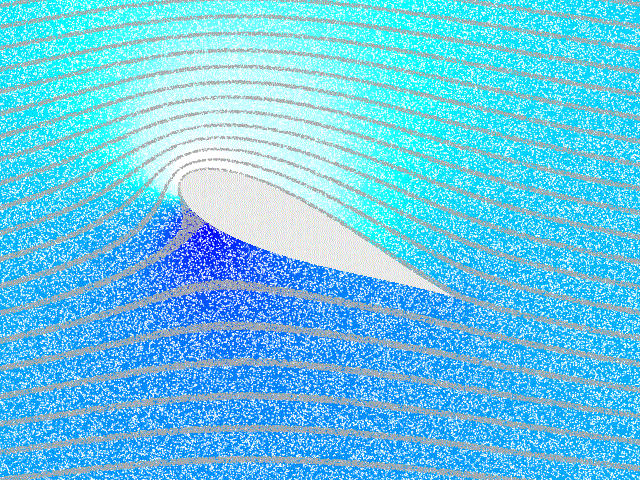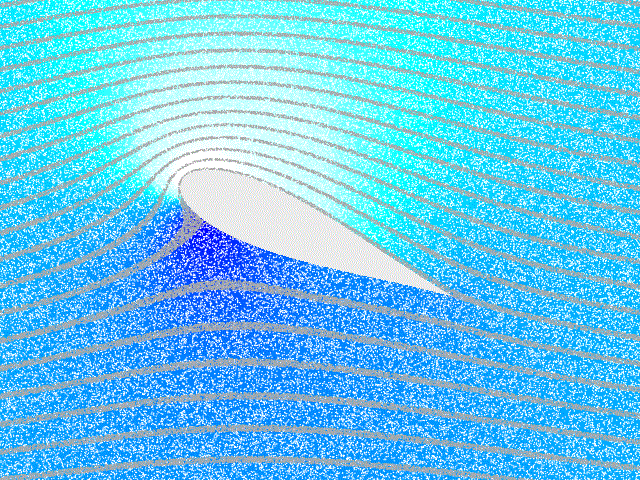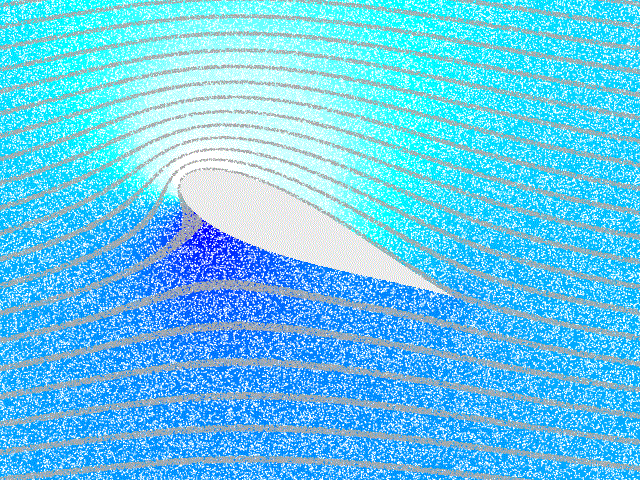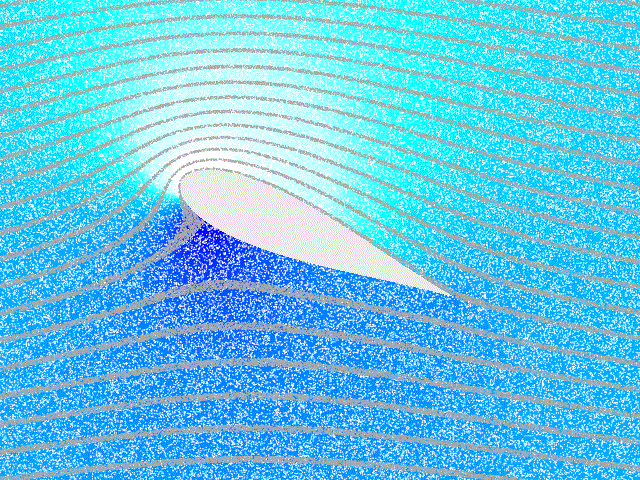

A wing slows the air underneath it, inreasing the pressure and generating lift.
In the right panel, air on the top of the wing is at increased speed and
reduced pressure, causing condensation of water vapor.
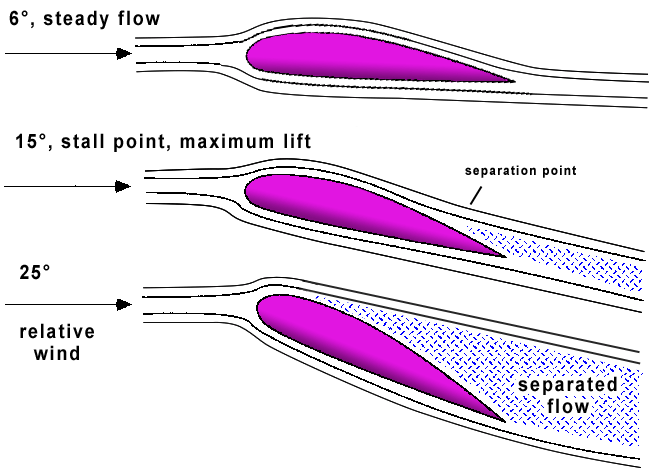
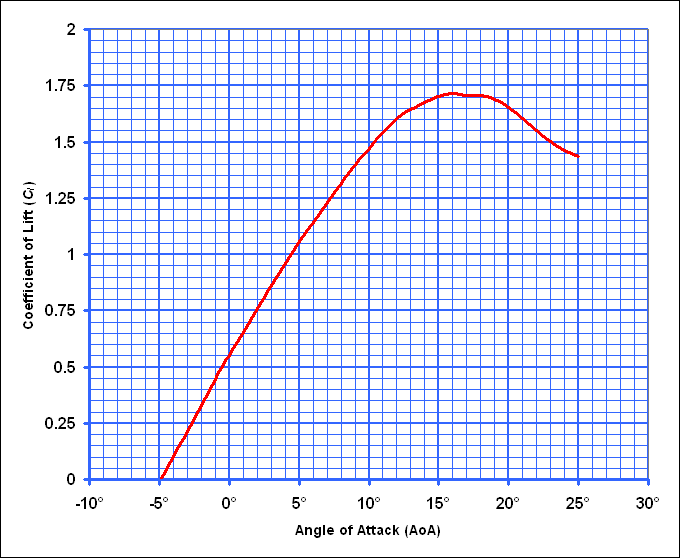

Lift incrases with wing angle, unless the angle is large enough for the airflowto stall.
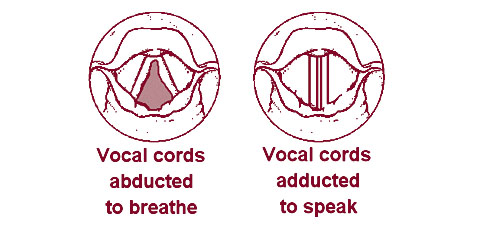
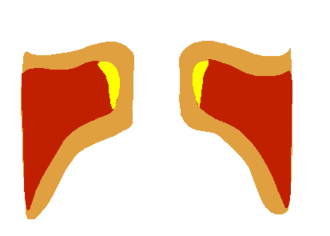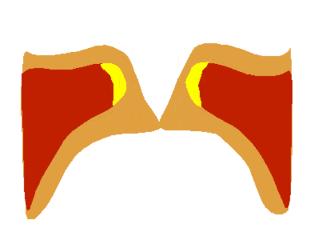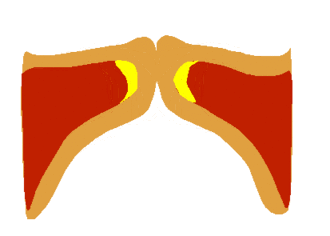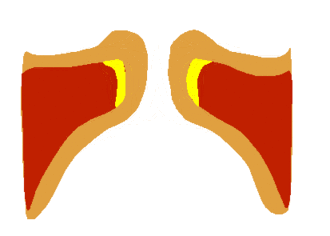
The vocal tract is around 17 cm long. For a half-open pipe this corresponds to
a resonant frequency of
Resonant frequency = WaveSpeed / (4 * Length)
= 340 / (4*.17)
= 500 Hertz
One has little control over the length of the vocal pipe but one can change the
shape, which is how vowels are formed.
Each of the two vocal chords functions like a string under tension. Changes in
muscle tension change the frequency of the vibration.
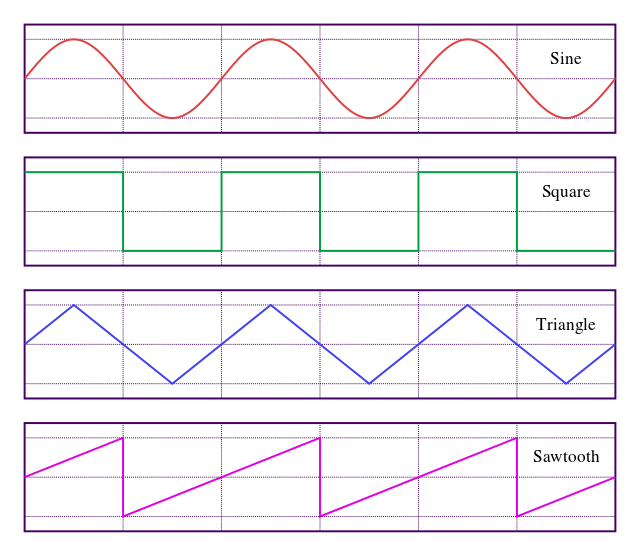
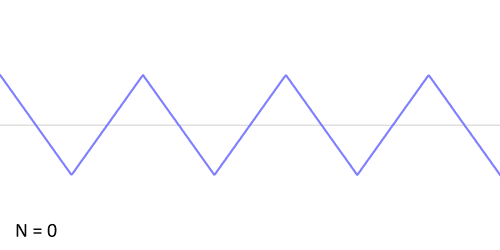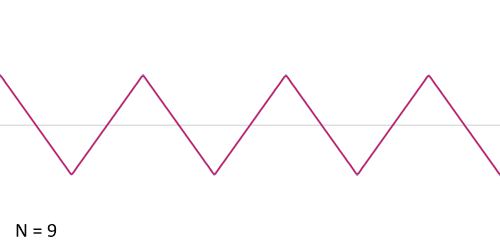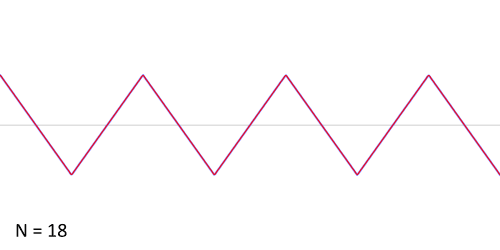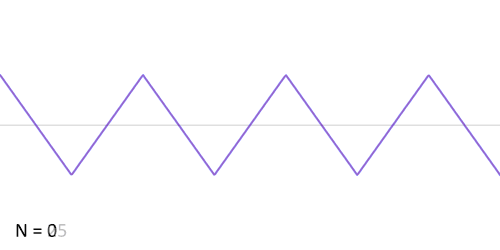
Audio file: Creating a triangle wave by
adding harmonics.
Lung pressure (Pascals)
Passive exhalation 100
Singing 1000
Fortissimo singing 4000
Atmospheric pressure is 101000 Pascals.
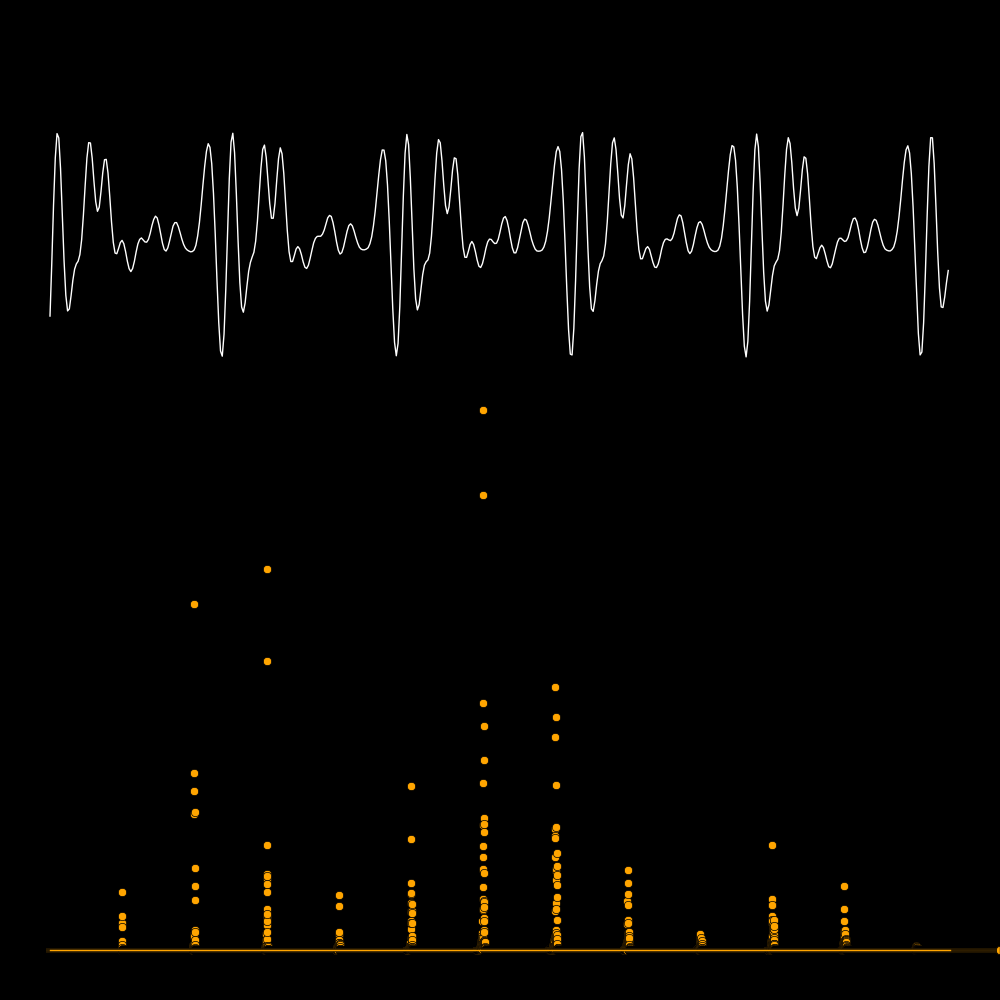
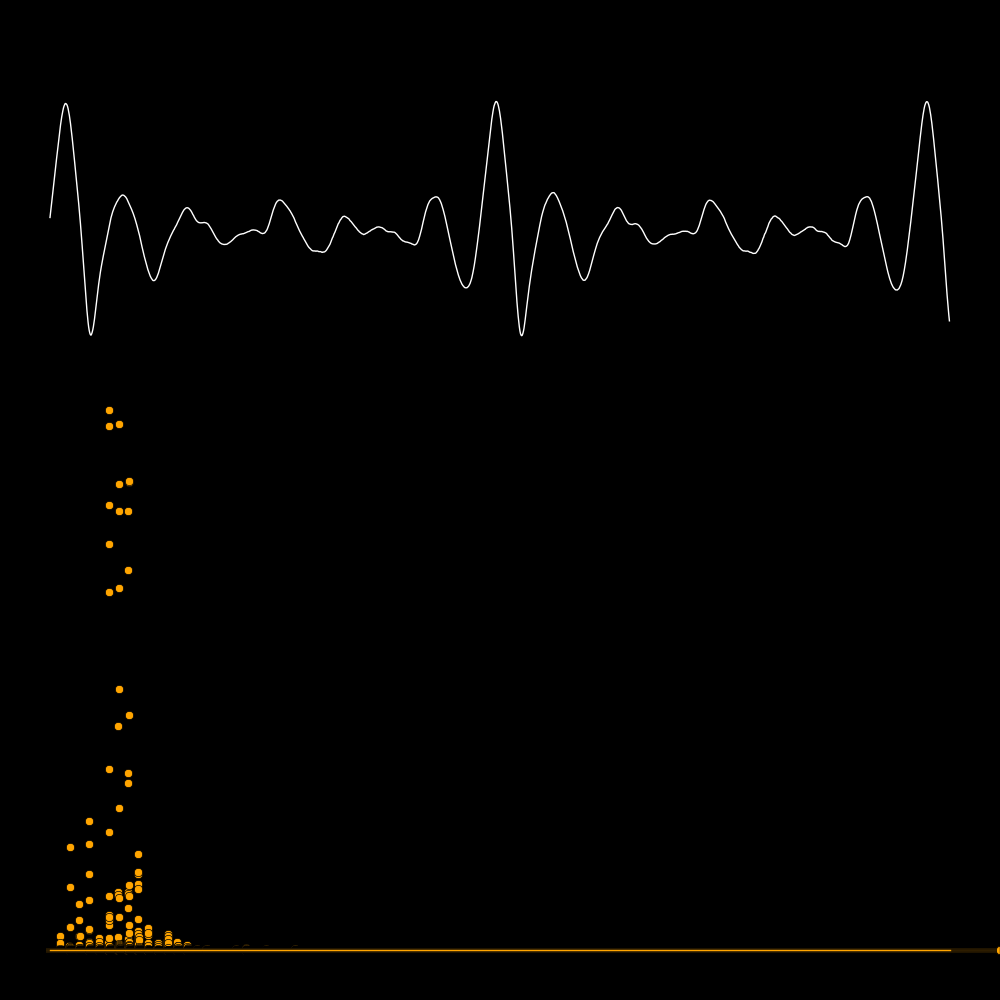
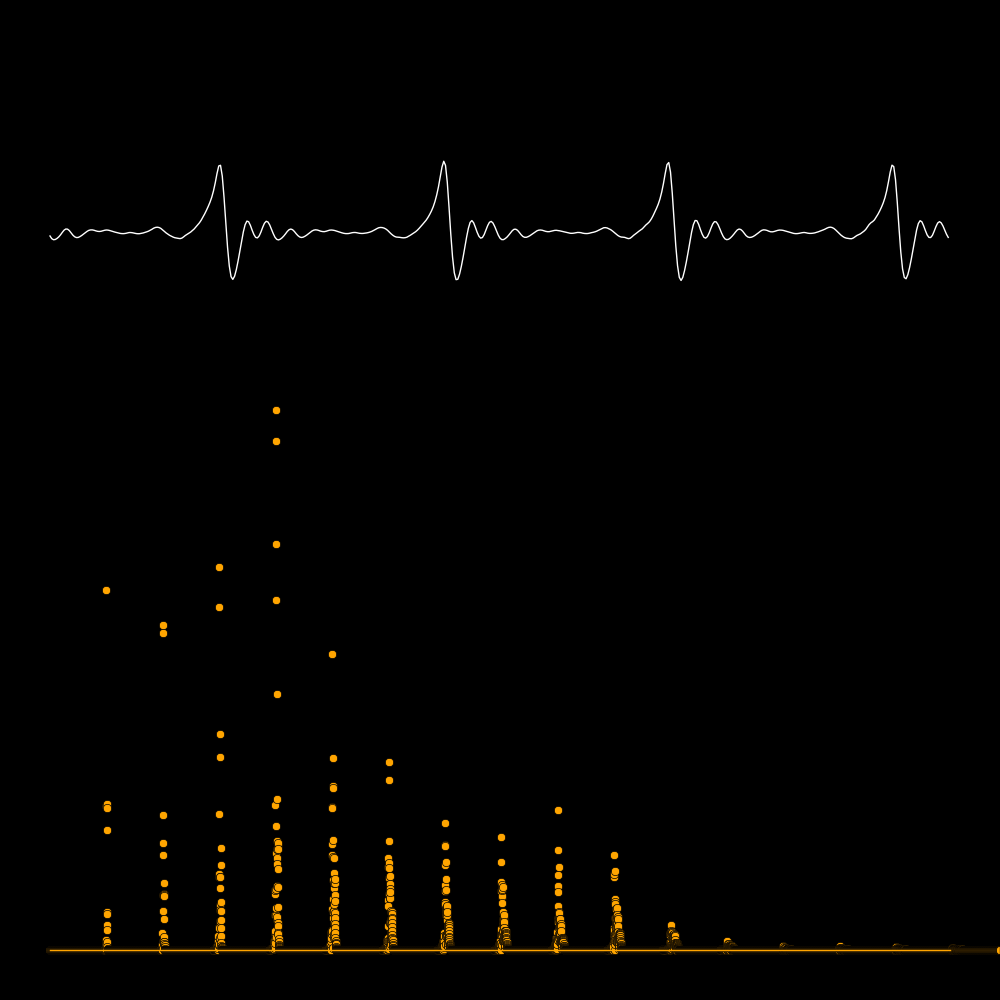
F = Wave frequency
Fmic = Sampling frequency of the microphone
Fny = Nyquist frequency
= Minimum frequency to detect a wave of frequency F
= 2 F
In the above figure the sampling frequency is equal to the Nyquist frequency,
or Fmic = 2 F. This is the minimum sampling frequency required to detect the
wave.

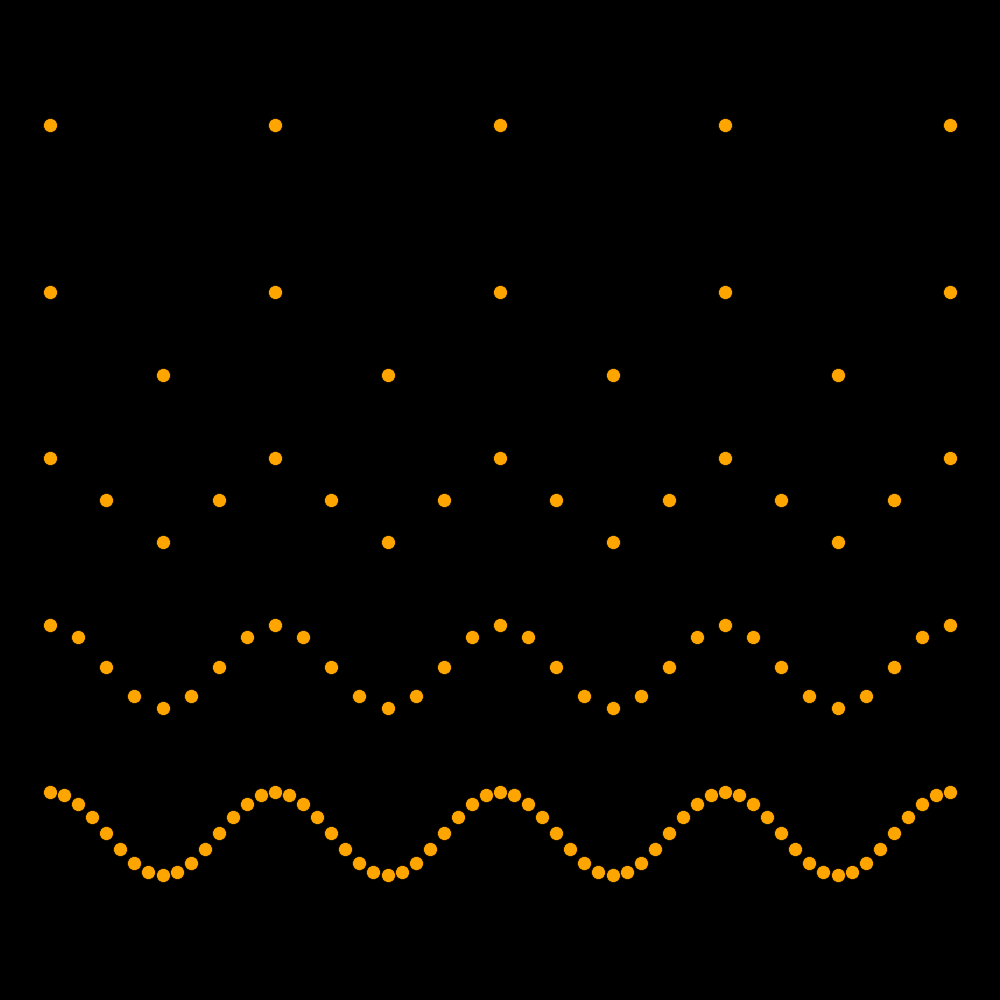
The Fourier transform takes A(T) as input and gives you the coefficients
C(F) and S(F).
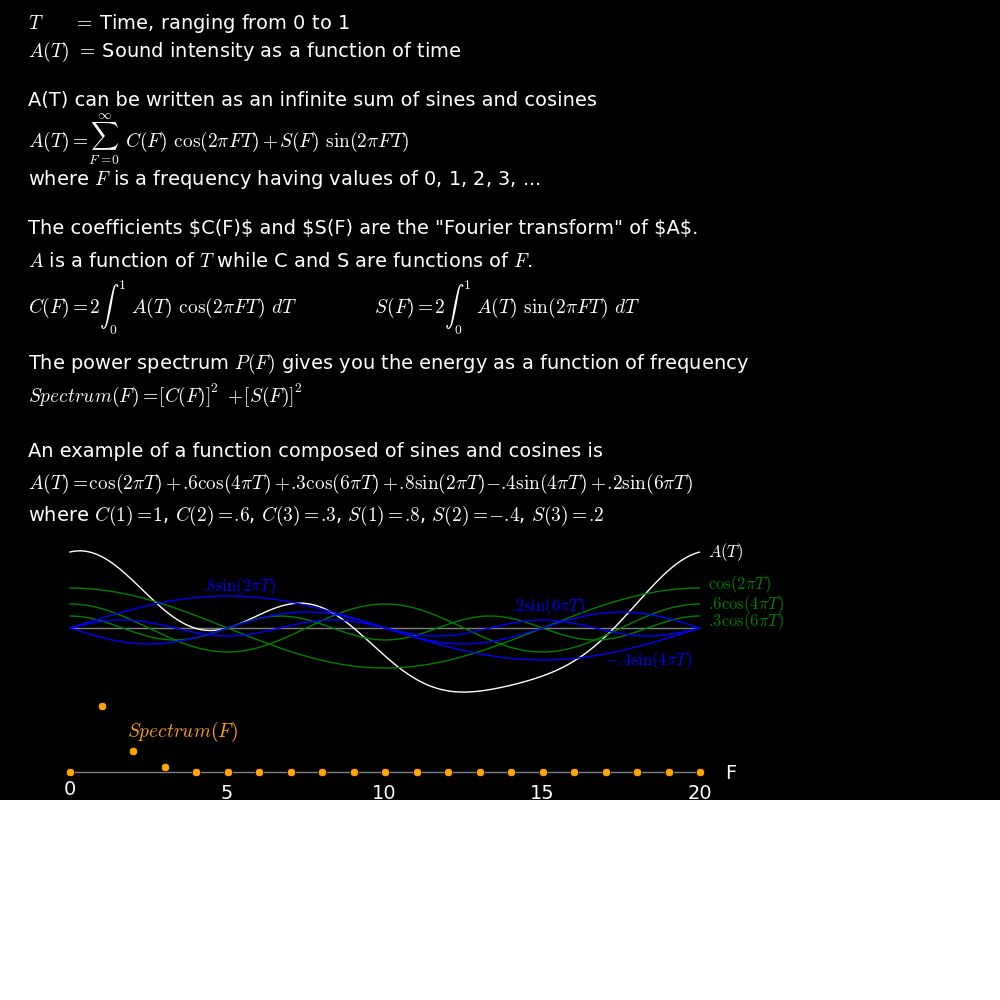
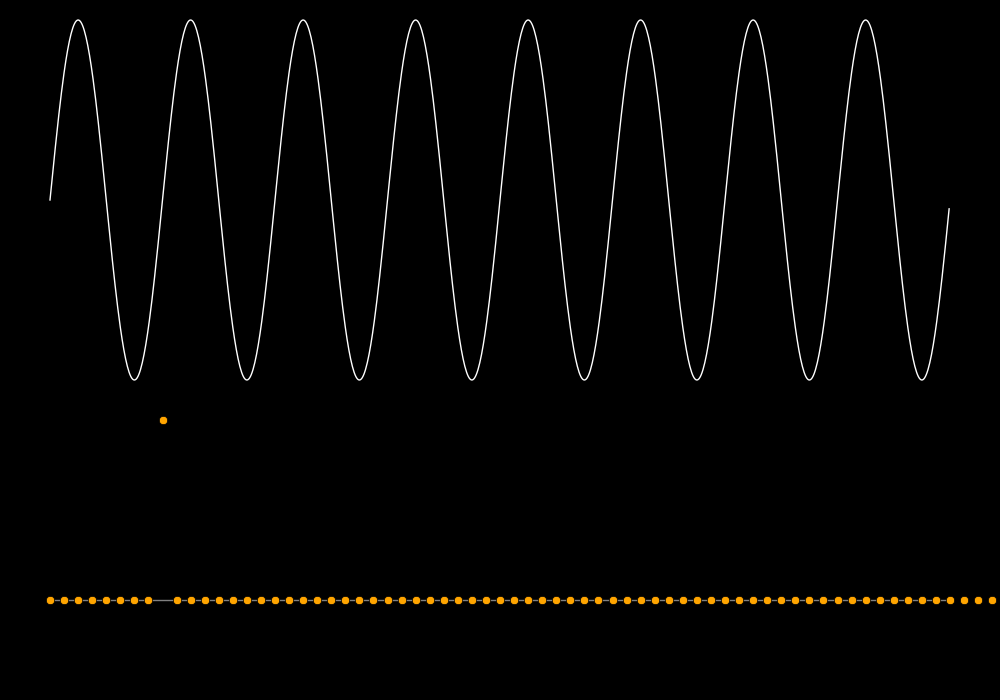
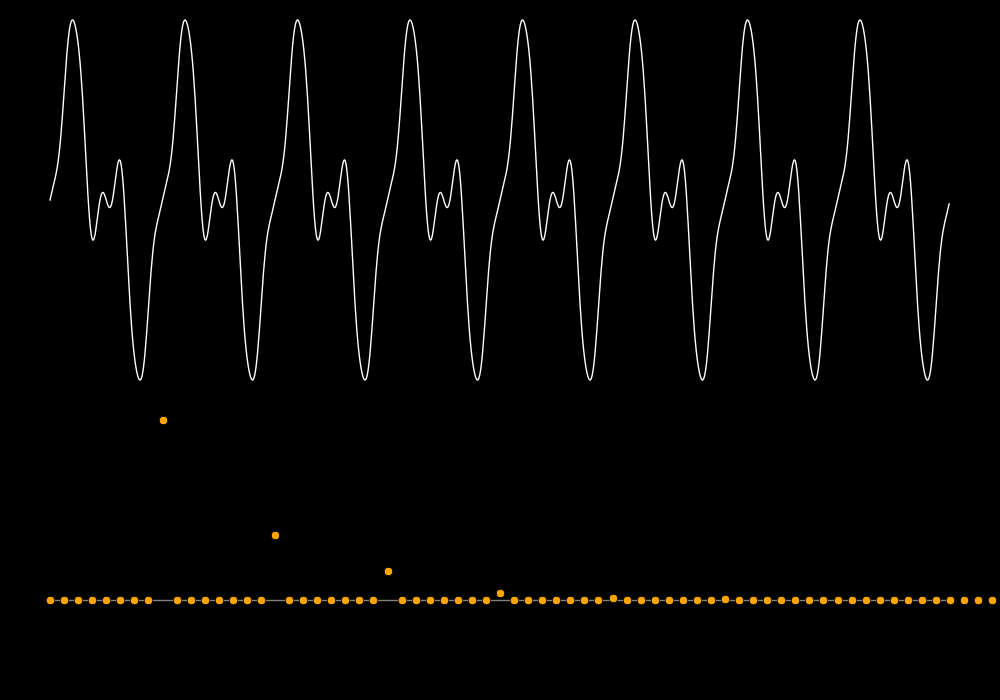
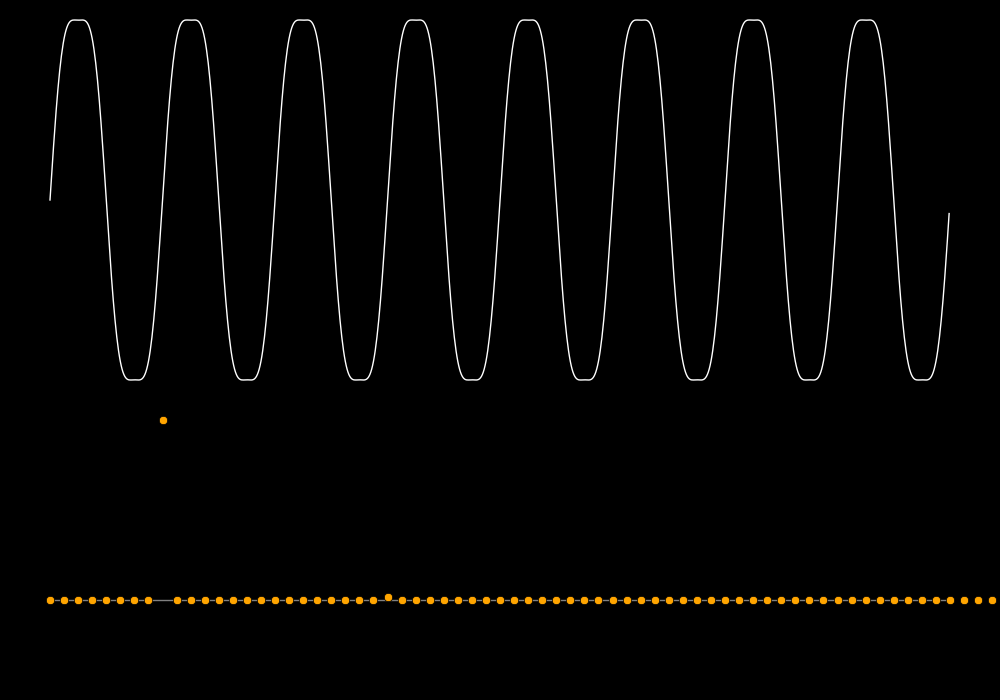
The sine wave has all its power at one frequency. A musical pitch is rich in
overtones.
The spectrum tells you how much energy is present at each frequency.
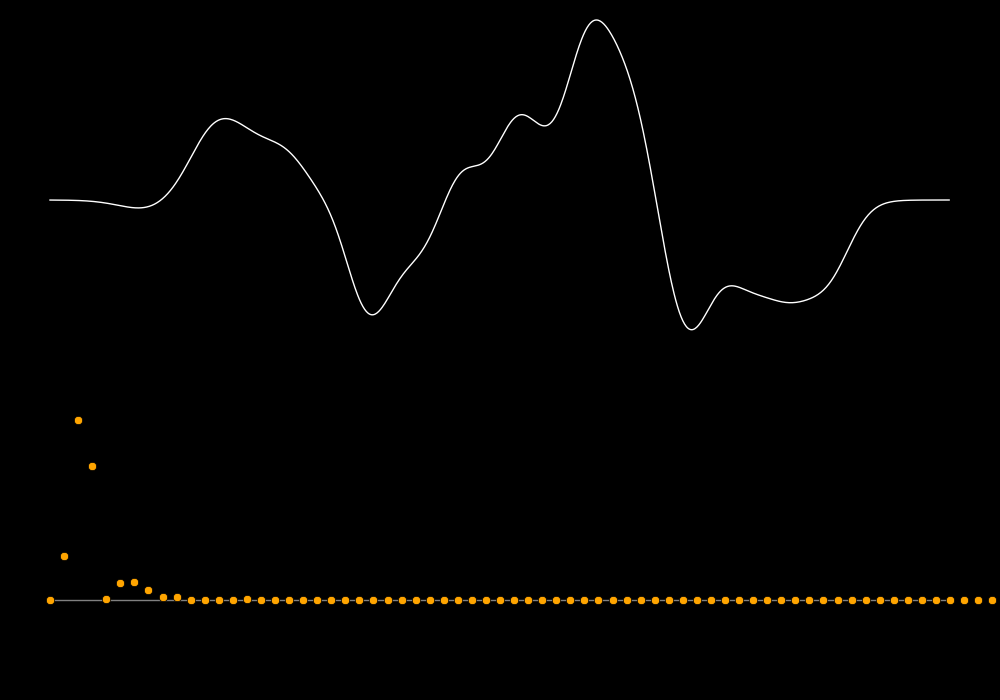
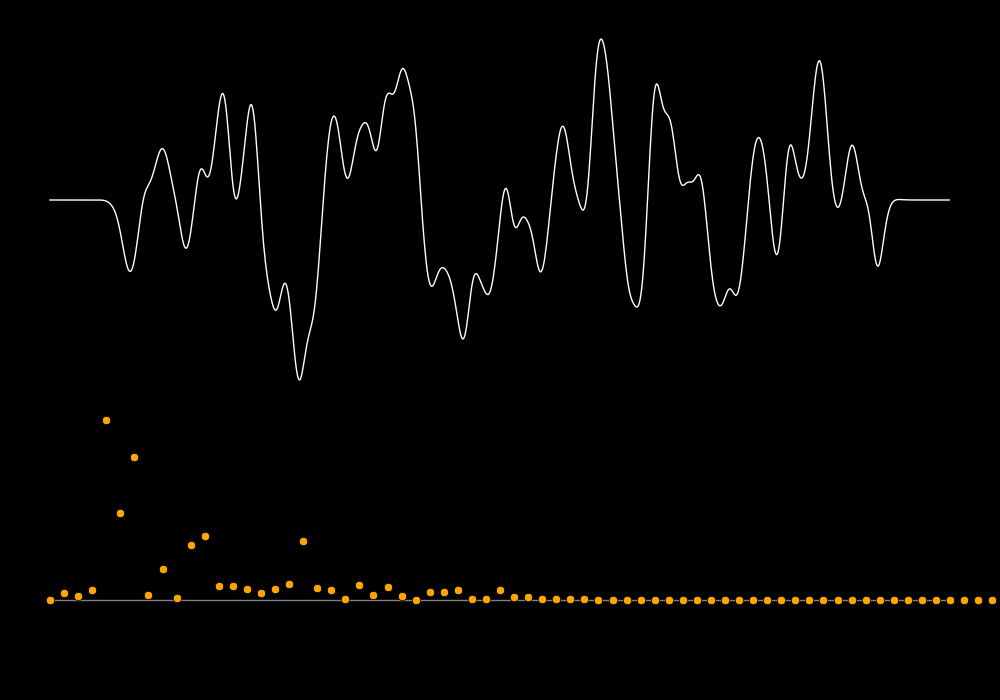
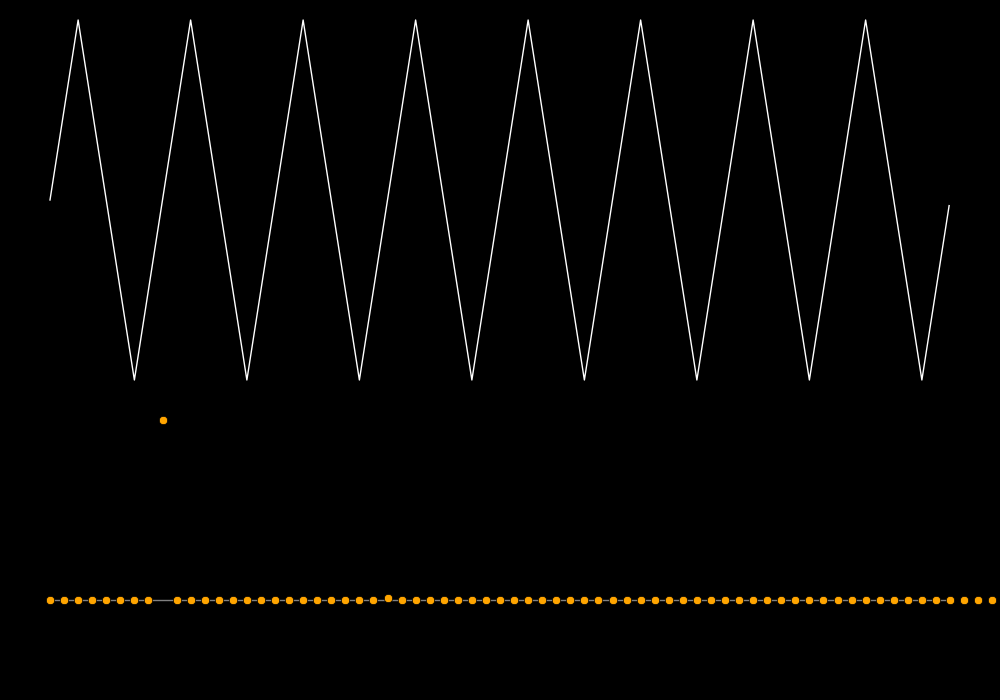
The spectrum tends to work well for smoothly-varying functions and
it tends to work poorly for jagged functions. For jagged structure the overtones
don't give you much information.
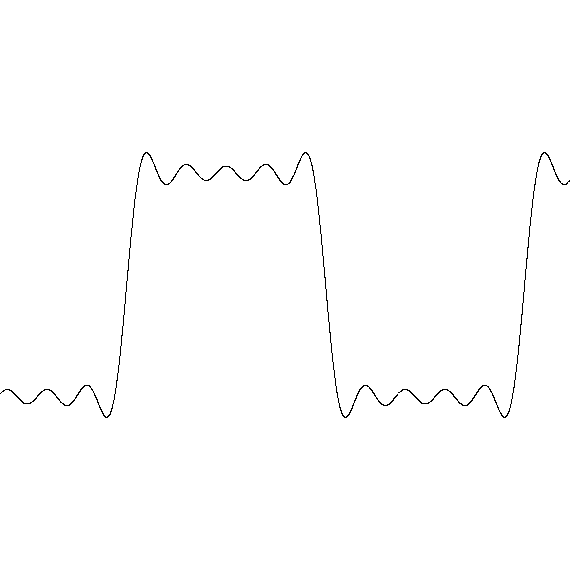
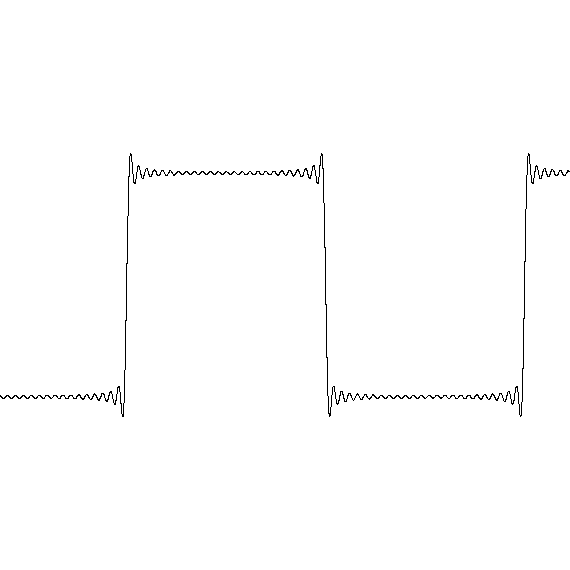
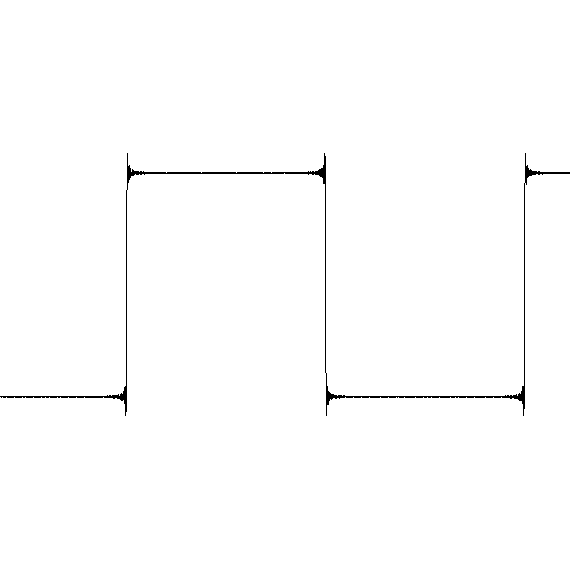
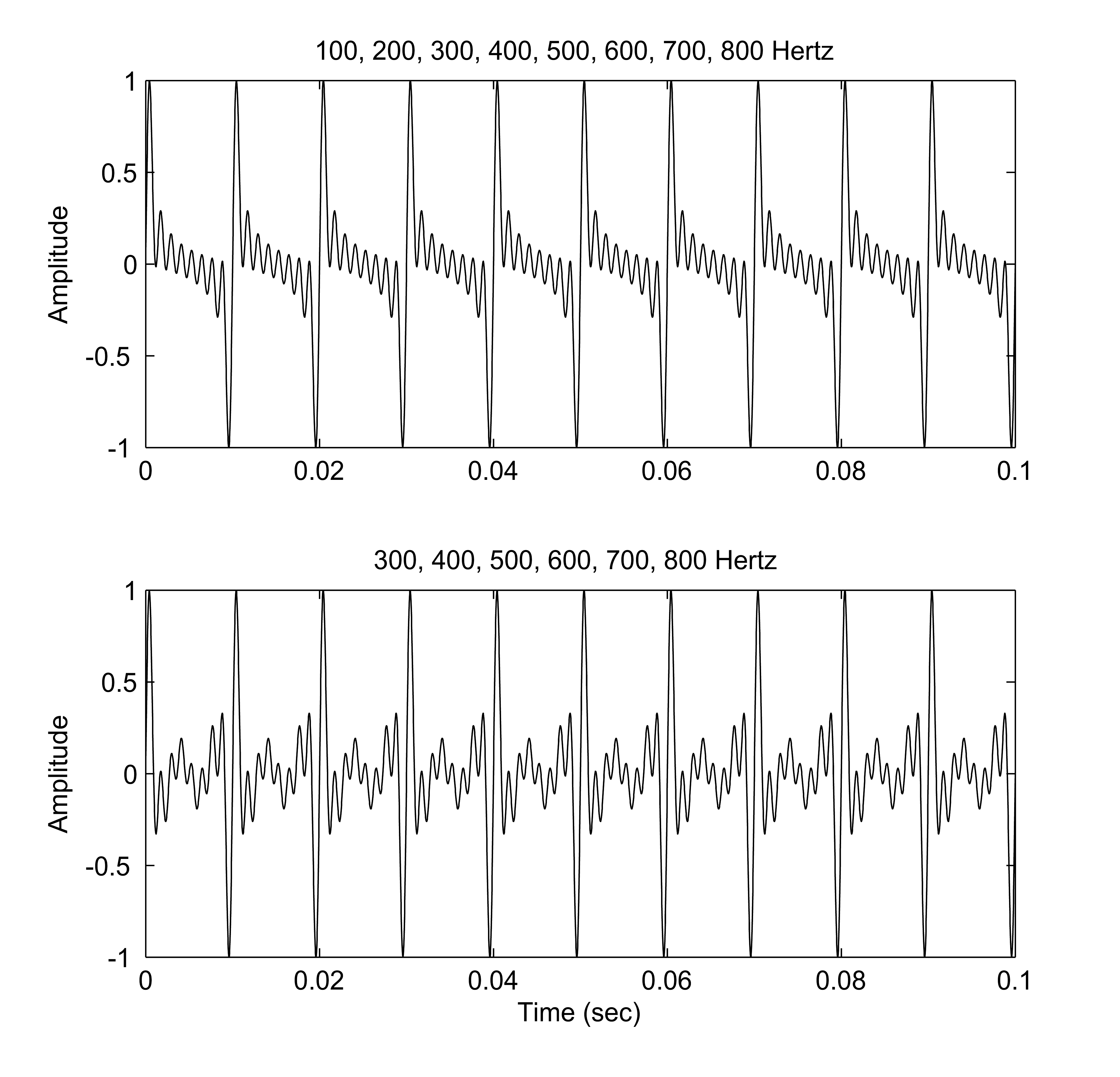
The top panel shows a sound with a frequency of 100 Hertz and with all
overtones present. In the bottom panel the 100 Hertz and 200 Hertz components
have been subtracted from the sound, but the 100 Hertz periodicity is still
evident in the waveform. Our ears can sense the fundamental frequency iven if
the fundamental overtone is absent.

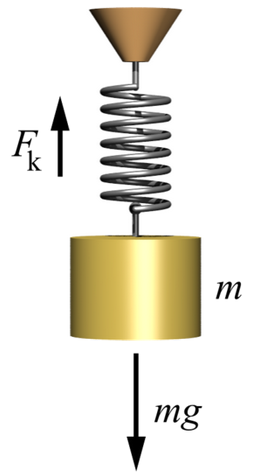
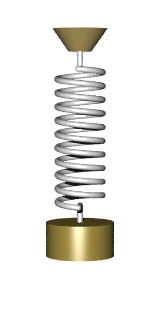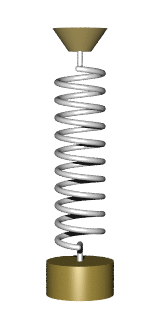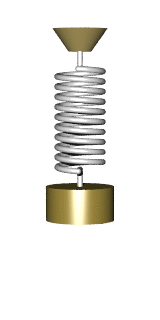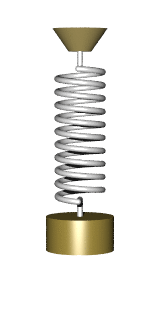
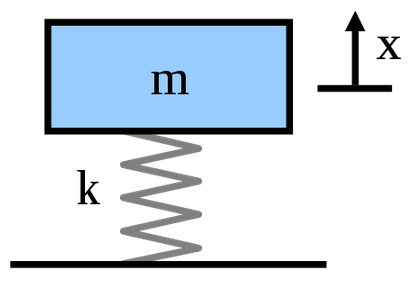
T = Time
X = Displacement of the spring when a force is applied
K = Spring constant
M = Mass of the object attached to the spring
Force = Force on the spring
= - K X (Hooke's law)
Solving the differential equation:
Force = M * Acceleration
- K X = M * X''
This equation has the solution
X = sin(2 π F T)
where
F = SquareRoot(K/M) / (2 π)
Wikipedia: Hooke's law
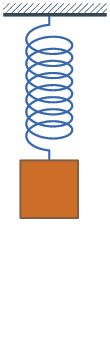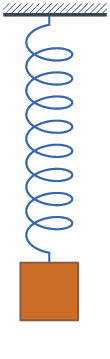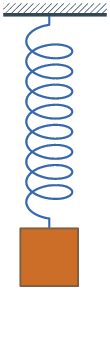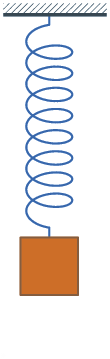

After a string is plucked the amplitude of the oscillations decreases with time.
The larger the damping the faster the amplitude decays.
T = Time for one oscillation of the string
Tdamp= Characteristic timescale for vibrations to damp
q = "Quality" parameter of the string
= Characteristic number of oscillations required for the string to damp
= Tdamp / T
In the above figure,
q = Tdamp / T = 4
The smaller the damping the larger the value of q.
For most instruments, q > 100.
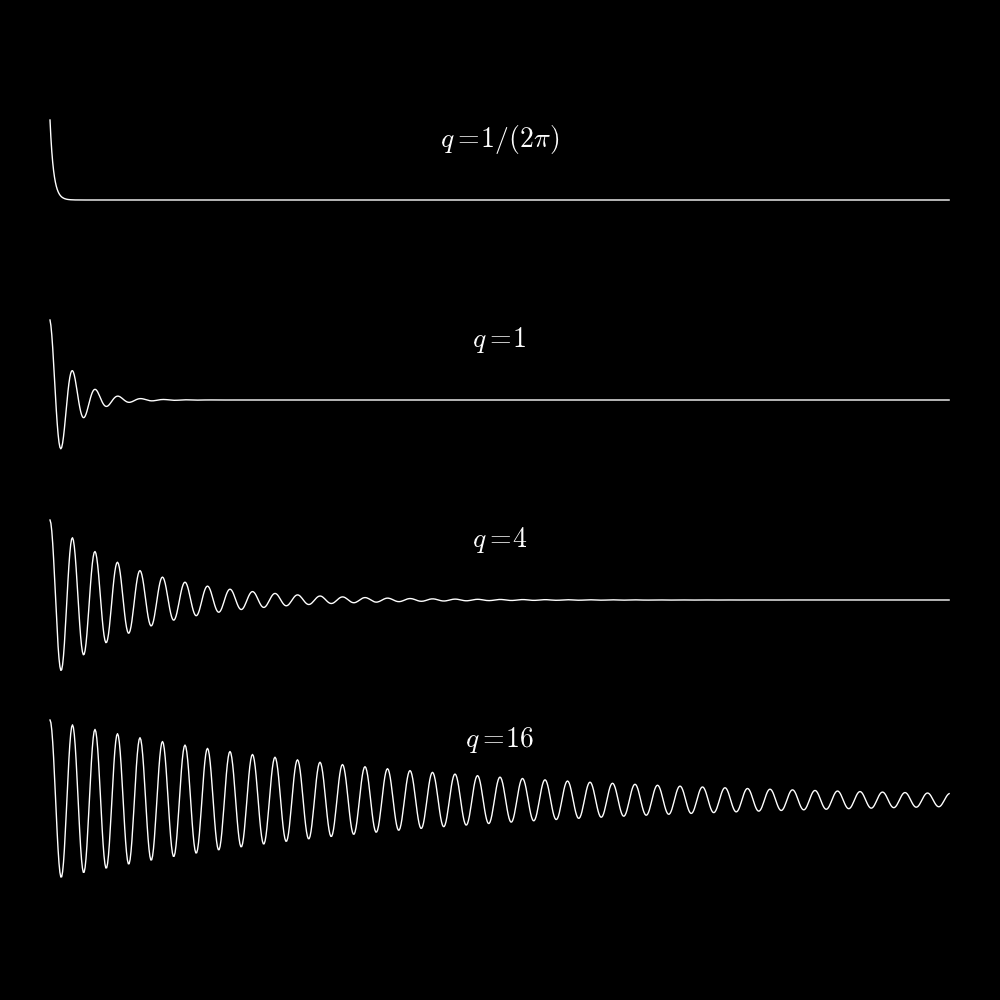
The above figure uses the equation for a damped vibrating string.
t = Time
X(t) = Position of the string as a function of time
T = Time for the string to undergo one oscillation if there is no damping
q = Quality parameter, defined below
Typically q>>1
F = Frequency of the string if there is no damping
= 1/T
Fd = Frequency of string oscillations if there is damping
= F Z
Z = [1 - 1/(4 π2 q2)]½
~ 1 if q>>1
A damped vibrating string follows a function of the form: (derived in the appendix)
X = exp(-t/(Tq)) * cos(Zt/T)
The consine part generates the oscillations and the exponential part reflects
the decay of the amplitude as a function of time.
q = (Timescale for damping) / (Time of one oscillation)
For example, you can record the waveform of a vibrating string and measure the
oscillation period and the decay rate.
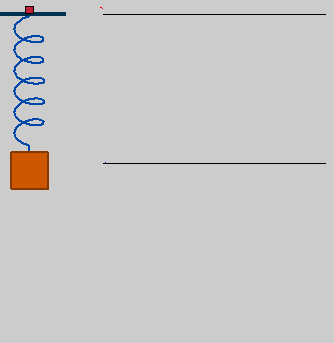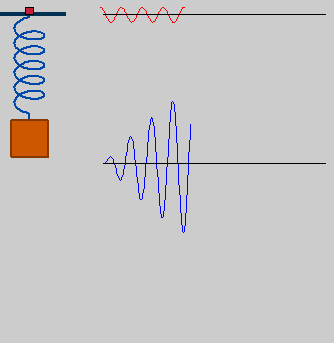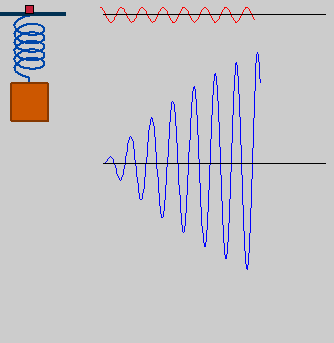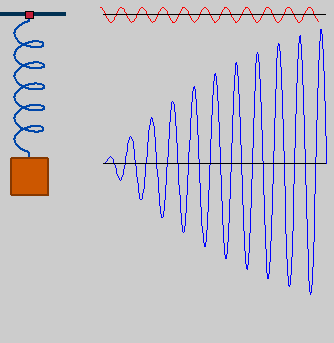

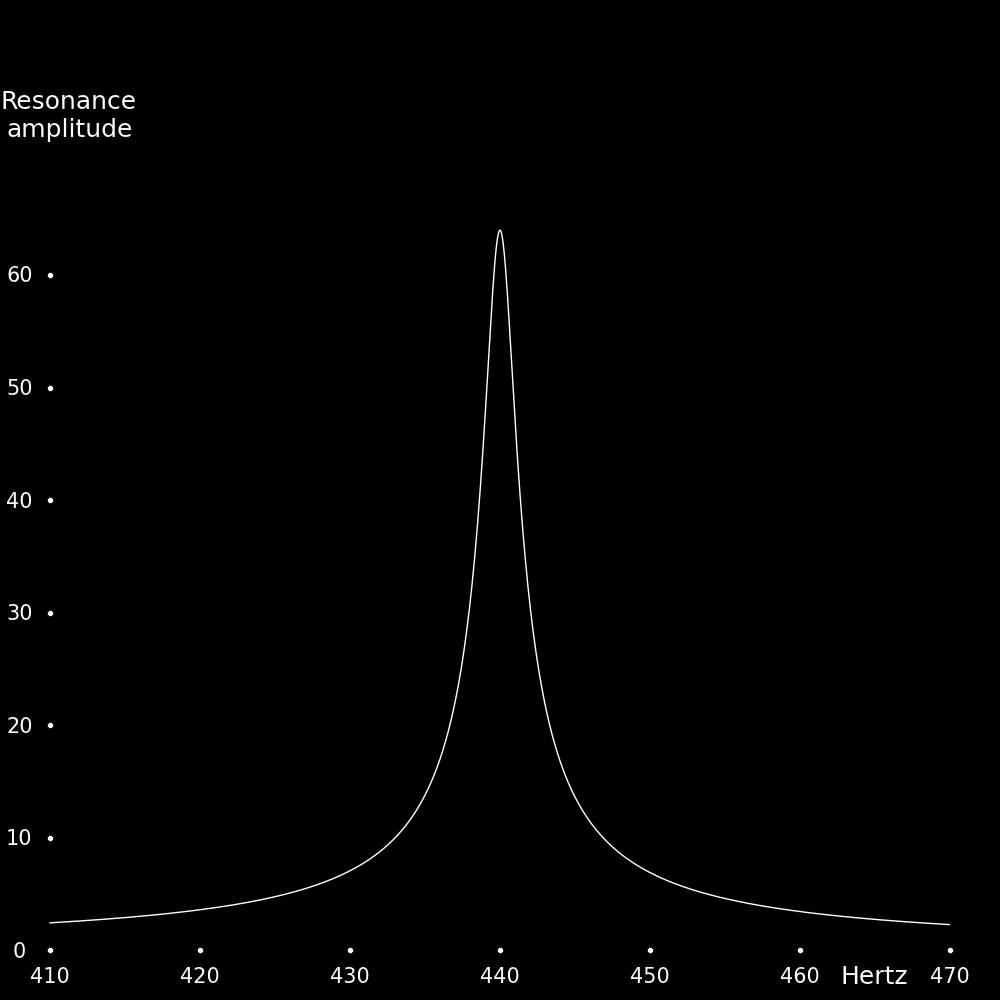
F = Frequency of the resonator
f = Frequency of the synthesizer
Fw = Characteristic frequency width for resonance
If |f-F| < Fw then the resonator vibrates
If |f-F| > Fw then the resonator doesn't vibrate
Resonance
simulation at phet.colorado.edu
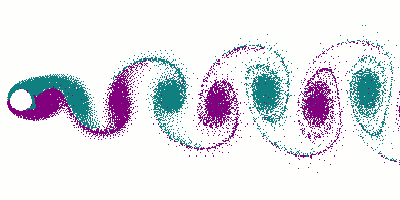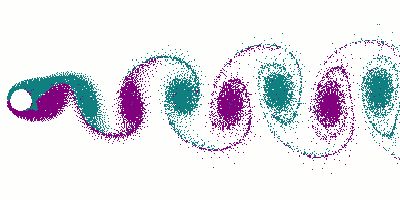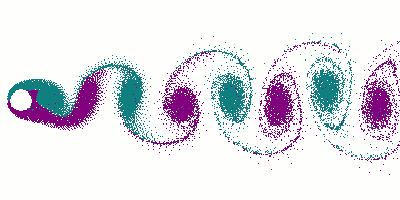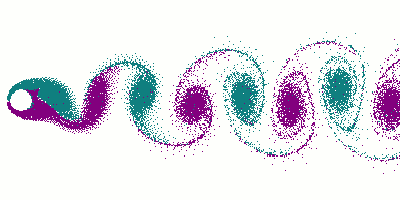

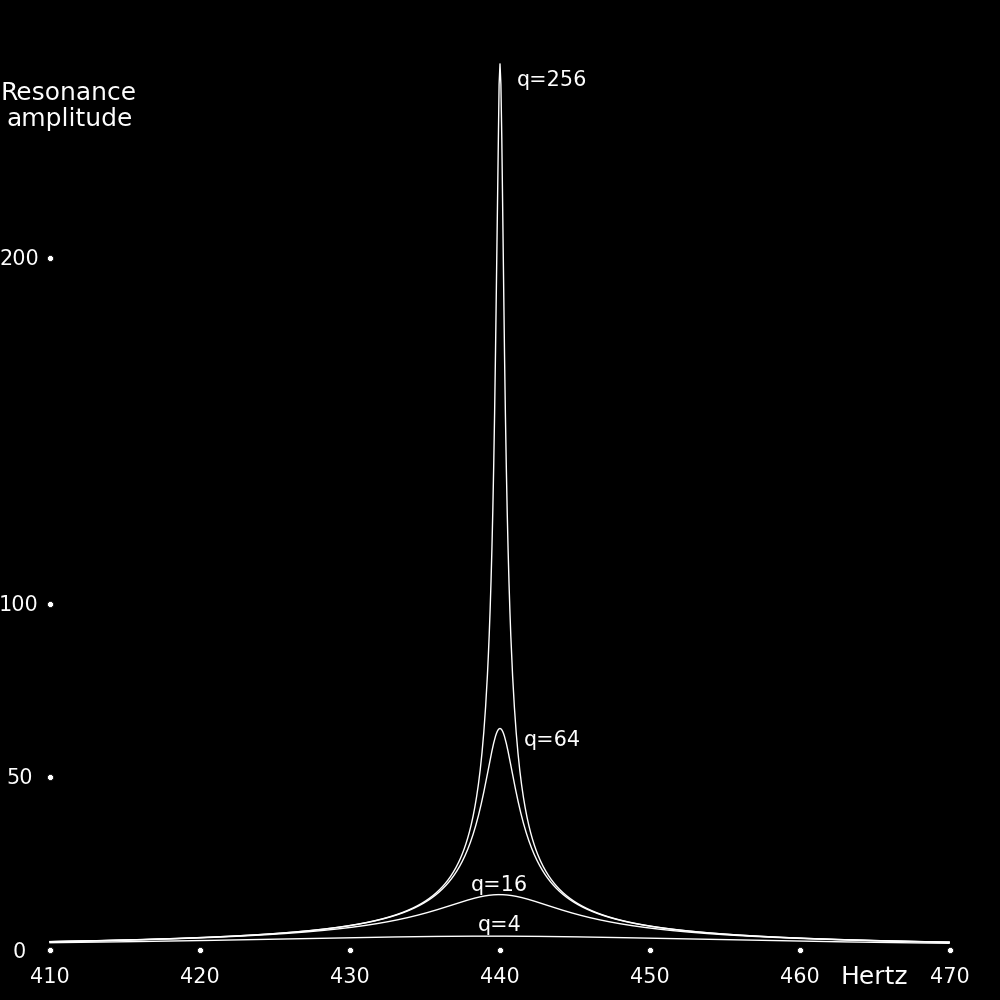
Amplitude of the resonance = Constant * q
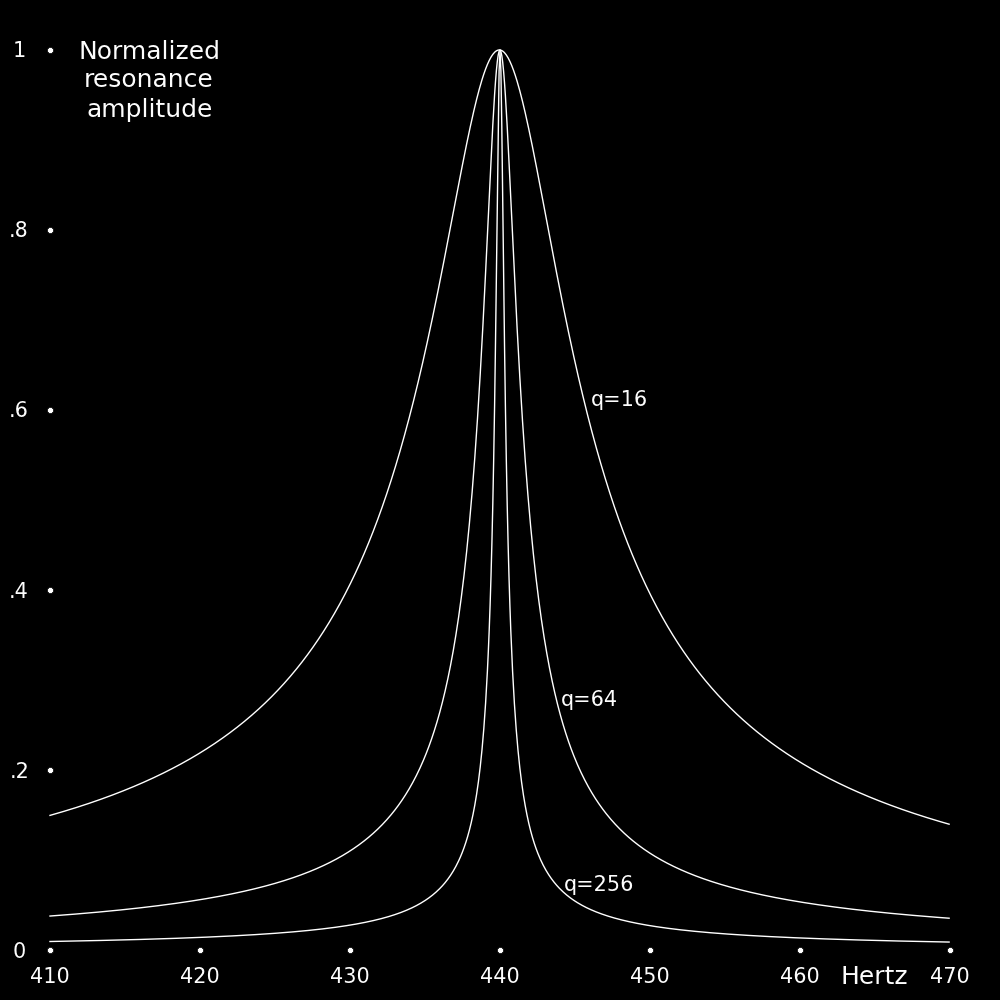
T = Time for one oscillation of the string
Tdamp = Characteristic timescale for vibrations to damp
q = Characteristic number of oscillations required for the string to damp
= Td / T
F = Frequency of the resonator
= 1/T
f = Frequency of the synthesizer
Fw = Characteristic frequency width for resonance (derived in appendix)
= F / (2 π q)
If |f-F| < Fw then the resonator vibrates
If |f-F| > Fw then the resonator doesn't vibrate
If q>>1 then
Width of the resonance = F / (2 π q)
Overtones can also excite a resonance. For example, if you play an "A" on the
G-string of a violin then the A-string vibrates. The open A-string is one
octave above the "A" on the G-string and this is one of the overtones of the
G-string.
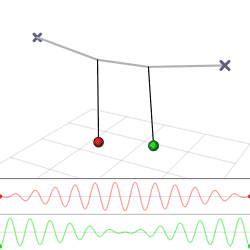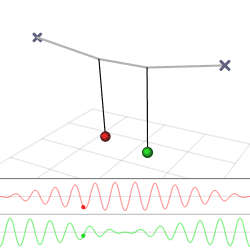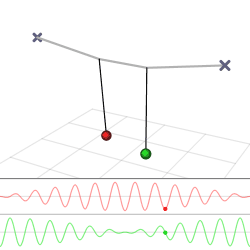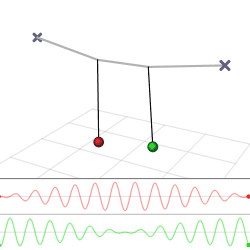
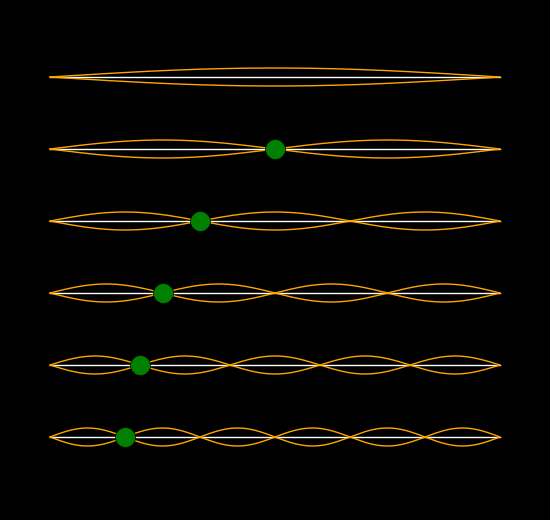
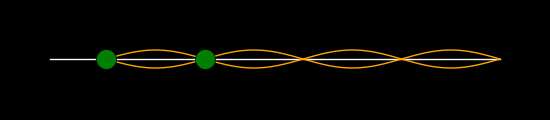

The note at the left of a string correspond to an open string.
In this figure the finger is places at the "E" on the A-string, which is marked
by the green dot. The figure shows the fundamental modes that are excited on
the E and A strings.
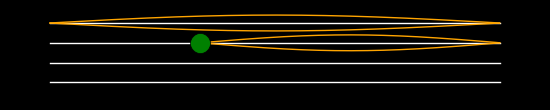
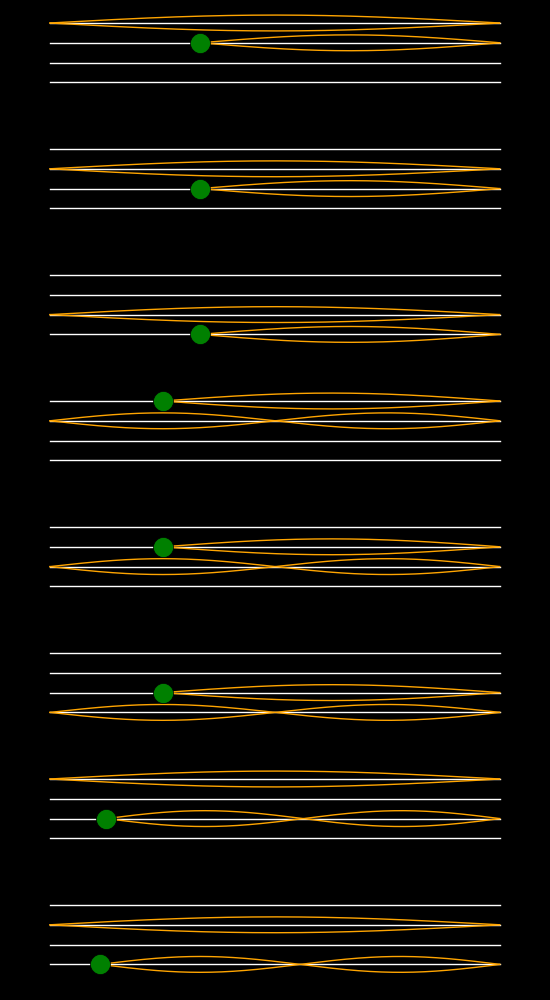
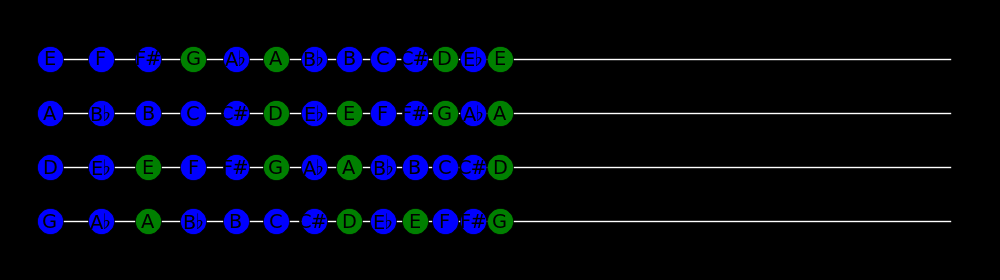
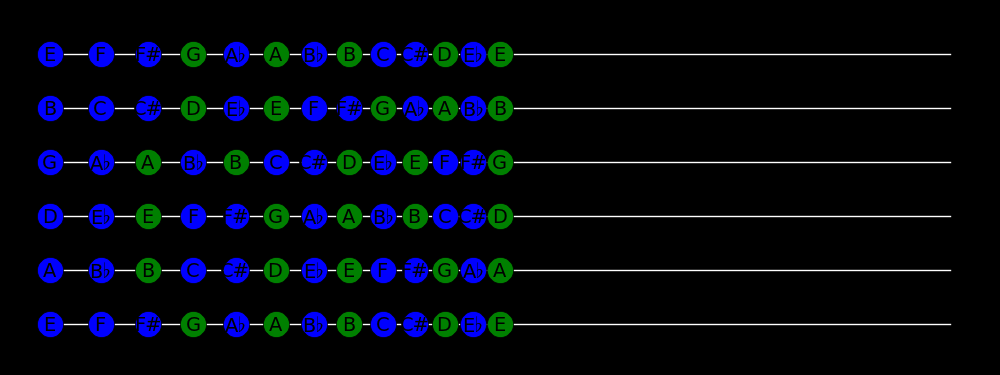
T = Time
X(T) = Vibration of a string as a function of time
X' = Time derivative of X
X'' = Second time derivative of X
F = Frequency of the string
q = Characteristic number of oscillations for damping to quell the vibration
The differential equation for a harmonic oscillator is
X'' = - 4 π2 F X
which is solved by
X = cos(2 π F T)
X oscillates with a frequency of F.
X'' = - 4 π2 F X - (2 F / Q) X'
which is solved by
X = exp(- F t / q) cos(2 π F Z t)
where
Z = [1 - 1/(4 π2 q2)]½
A = Amplitude for vibrations when the string is forced with frequency f
F = Resonant frequency of a string
Fw = Characteristic width of the resonance
A-2 = F4 / q2 + π2 (f2 - F2)2
The amplitude reaches its peak when F=f. In this case,
A = q / F2
The amplitude of a resonance is proportional to q.
F4 / q2 = π2 (f2 - F2)2
Let f = F + Fw, where |Fw| << F
f2 - F2 = F2 + 2 F Fw + Fw2 - F2
~ 2 F Fw
Hence
F4 / q2 ~ 4 π2 F2 Fw2
Fw ~ F / (2 π q)
The width of the resonance Fw is proportional to F and inversely proportional to q.

T = Time over which the measurement is made
N = Number of crests occurring in a time T
F = N/T
dF = Uncertainty in the frequency measurement
= 1/T
Suppose the number of crests can only be measured with an uncertainty of +-1.
The uncertainty in the frequency is dF = 1/T. The more time you have to observe
a wave the more precisely you can measure the frequency.
dF T >= 1
h = Planck's constant
= 6.62e-34 Joule seconds
Q = Particle momentum
W = Particle wavelength
= h / Q
F = Particle wave frequency
E = Particle energy
= h F
dE = Uncertainty in the particle energy
dF = Uncertainty in the particle frequency
dT = Time interval
Uncertainty principle for particle energy:
dE dT >= h / (4π)
Using dE = h dF,
dF dT >= 1 / (4π)
T = Duration of a note
Fbeat = Frequency resolution for just-intonation
= 1/T
F = Frequency of a note
T = Duration of a note in seconds
q = Quality parameter for the resonator
= Characteristic number of times a resonator oscillates before losing
its energy to damping
Fhear = Frequency width for human perception
= .006 F
= F / 170
Fres = Frequence width for a resonance at a frequency of F
= F / (2 π q)
Fbeat = Frequency width for detecting beat frequencies
= 1 / T
Fjust = Frequency resolution for just-intonation
= Fbeat
= 1 / T
Func = Frequency precision from the uncertainty principle
= Frequency precision for a computer tuner
= 1 / T
The larger the value of F, the more difficult it is to play just-intonation.
X = Length of a violin string
= .32 meters
x = Length of the active part of the string between the finger and the bridge.
F = Frequency of the open string
= 660 Hertz for an E string
f = Frequency of the note being played by the finger
I = Index of the note being played.
= 0 for an open string
= 1 for a half step
= 12 for an octave
D = Distance between the peg end of the string and the finger
= X - x
f x = F X = Constant
f = F 2I/12
x = X 2-I/12
D = X (1 - 2-I/12)
If I=1, D = 18 mm
If I=.1, D = 1.8 mm
If F=660 and f=661,
x/X = 660/661
D = .48 mm
There is little margin for error on an E-string.
If F=130 and f=131,
x/X = 130/131
D = 2.9 mm
F = Frequency of a note
T = Duration of a note
Fhear = Frequency resolution for human hearing
= F/170
Func = Frequency resolution from the uncertainty principle
= 1/T
Thear = Duration of a note for which Fhear=Func
= 170/F
Frequency resolution is limited by either by Fhear or by Func, whichever is
larger.
If (T < Thear) then the precision is limited by the uncertainty principle.
If (T > Thear) then the precision is limited by the ear.
For a given frequency F, the values for Thear and Tres are (Tres is defined below)
F Tres Thear
55 .49 3.1
110 .25 1.6
220 .12 .77
440 .061 .39
880 .031 .19
1760 .015 .10
For low-frequency notes it takes a long time for the pitch to develop.
F = Frequency of a note
T = Duration of a note
q = Quality parameter for the resonators in the ear
Fhear = Frequency resolution of the ear
= F / 170
Thear = Characteristic timescale for the ear to sense pitch
= 1 / Fhear
= 170 / F
Fres = Frequency resolution of a resonator
= F / (2 π q)
Tres = Time for a resonator to activate
= q * (Duration of one cycle of the resonator)
= q / F
If we set Fhear=Fres then
F / 170 = F / (2 π q)
q = 170 / (2 π)
= 27
The activation time for the resonators in the ear is
Tres = q / F
= 27 / F
Thear / Tres = 2 π
If (T < Tres) then the ear resonators are not fully activated and the note sounds
less loud than if it had been played longer.
F = Note frequency
Tstart = Minimum start time of a note
= 1/F
Stabilizing the start of a note
Tstart = Minimum start time of a note
= 1/F
Tres = Time for the resonators in the ear to activate
= 27/F
Thear = Duration of a note for which Fhear=Func
= 170/F
Between Tstart and Tres the organ of Corti is amplifying the resonances.
After Tres the organ of Corti is narrowing the resonances to refine the
frequency measurement.

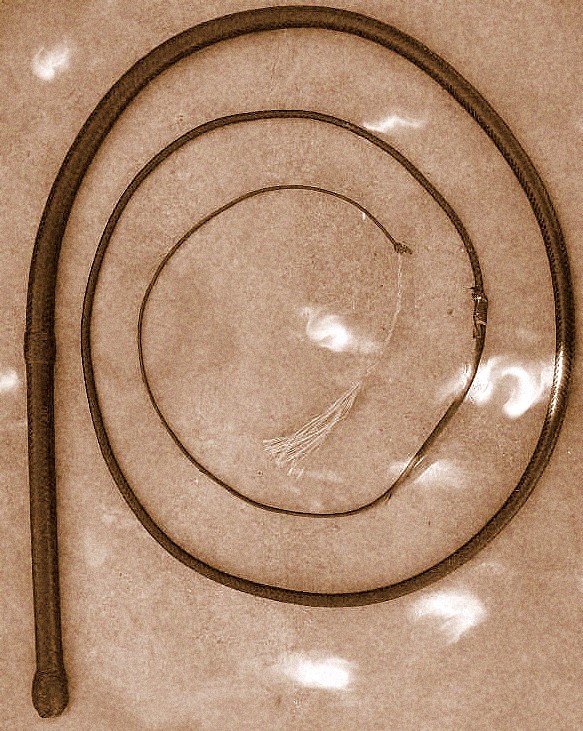
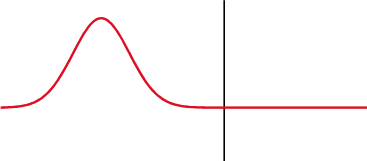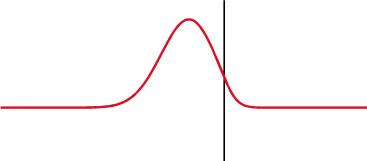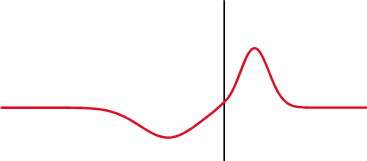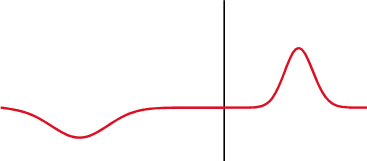




Slow motion baseball pitch

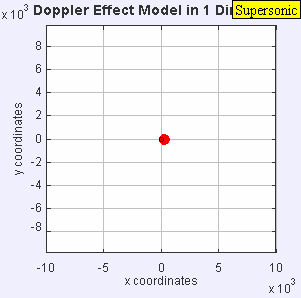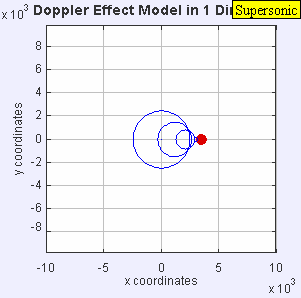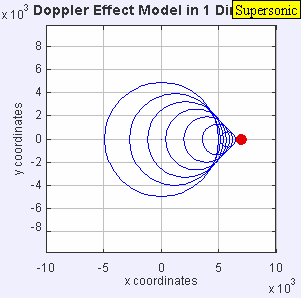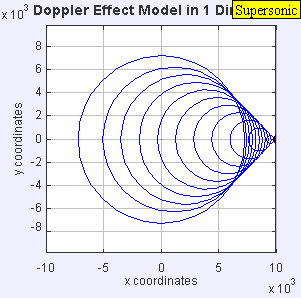
F = Frequency emitted by the sourcer
f = Frequency perceived by the listener
Vs = Velocity of the source
Vr = Velocity of the receiver
V = Speed of sound
= 340 meters/second
f = F (V + Vr) / (V + Vs)
A shock is the Doppler effect taken to the extreme, where the perceived frequency
becomes infinite and all waves arrive at the same time.
f ~ F (1 + 1/340)
This is half the frequency width of human hearing. The Doppler effect is not
noticeable in an orchestra.















-2500 An ensemble of lyres was played in the ancient city of Ur, including
lyres, harps, flutes, and reed instruments.
1000 Bowed instruments first developed, such as the Lyre
1200 The guitar comes into use in Europe
1555 Amati develops the four-string violin
1700 Cristofori develops the first piano, an instrument where the string is
struck by a hammer. Early pianos had 5 octaves
1785 Tourte develops the modern bow
1810 Broadwood develops a 6-octave piano
1820 Broadwood develops a 7-octave piano
1821 Erard develops the double-escapement mechanism for the piano, a
device that permitted repeating a note even if the key had not yet risen
to its maximum vertical position. This facilitated rapid playing
of repeated notes.
1835 Tuba invented
1847 Boehm advances the design of the flute, including a switch from wood to metal
1931 Beauchamp builds the first electric guitar
500 - 1400 Medieval
1400 - 1600 Renaissance
1600 - 1760 Baroque Monteverdi, Vivaldi, Bach, Handel
1720 - 1770 Galant Gluck
1730 - 1820 Classical Mozart
1780 - 1910 Romantic Beethoven, Brahms, Wagner
1890 - Now Modern Prokofiev, Shostakovich











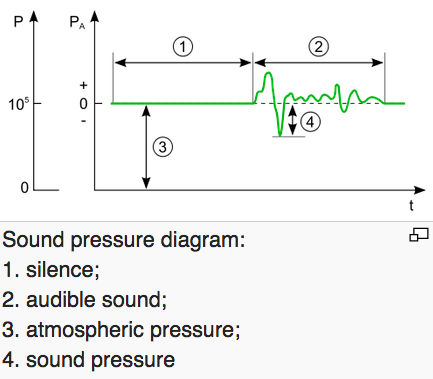
For air at sea level,
Density = 1.2 kg/meters^2
Pressure = 101300 Pascals (Newtons/meter^2)
= 14.7 pounds/inch^2
Temperature = 288 Kelvin (Mean value)
= 15 Celsius
Patm = Atmospheric pressure
Ptotal = Total pressure
Pfluct = Pressure fluctuation
= Ptotal - Patm
Prms = Characteristic amplitude of pressure fluctuations
Prms is defined as the "root-mean-squared" amplitude of pressure fluctuations.
Prms = ( Time average of Pfluct^2 )^{1/2}
For example, if a sound wave is a sine wave with an amplitude of "A" then the
pressure Pttotal as a function of time is
F = Wave frequency
T = Time
Ptotal = Patm + A * sin(2 Pi F T)
Prmsp = A / Squareroot(2)
Prms has the same magnitude as "A".
P = Air Pressure
Prms = RMS fluctuations in the pressure
D = Air Density
Drms = RMS fluctuations in the density
Vrms = RMS fluctuations in the velocity
Vsound= Speed of sound
Gamma = Adiabatic number
= 7/5 for air
E = Energy per volume in sound waves
For sound waves,
Vrms / Vsound = Drms / D = Prms / P / Gamma
E = .5 D Vrms^2
= .5 D Prms^2 Vsound^2 / P^2 / Gamma^2
The energy density of sound is proportional to Prms^2.
Patm = Atmospheric pressure
= 101300 Pascals
Prms = Characteristic amplitude of pressure fluctuations (Pascals)
Pref = Reference pressure
= Lower limit of human sensitivity
= The faintest sound we can hear
= .00002 Pascals
Dec = Sound pressure level expressed in decibels
= 10 * LogBase10(Prms^2/Pref^2)
Pref represents the limit of human sensitivity. The faintest sound that humans
can hear has
Prms = Pref
Dec = 0
Table of sound pressures.
Prms Decibels
101300 194 Supersonic shock
10000 174 Rifle at a distance of 1 meter
1000 154 Jet engine
100 134 Threshold of pain
10 114 Vuvuzela at a distance of 1 meter
1 94 Hearing loss occurs from long-term exposure at this level
.1 74 Loud conversation
.01 54 Normal conversation
.001 34
.0001 14 Rustling leaves
.00002 0 Threshold of human hearing
103 Violin
92 Cello
112 Piccolo
111 Flute
94 Oboe
103 Clarinet
106 French horn
114 Trombone
106 Timpani
Our ears perceive loudness logarithmically. The loudness we perceive is proportional
to the intensity in decibels. For example, a sound of 80 decibels appears louder than
a sound of 70 decibels by the same margin that a sound of 70 decibels sounds louder
than a sound of 60 decibels.
Data for instrument loudness
Power
(Watts)
Saturn V rocket 100000000
Turbojet aircraft 100000
Turboprop aircraft 100
Machine gun 10
Large pipe organ 10
Orchestra 1
Noisy conversation .00001
Quiet conversation .000000001
Whisper .0000000001
Human breath .00000000001
Wikipedia: Sound power
Power = Sound power at the source in Watts
R = Distance to the source
Vsound = Speed of sound
Flux = Sound energy flux at a distance R from the source
= Power / (4 Pi R^2)
E = Sound energy density
= Flux / Vsound
= Power / (4 Pi R^2) / Vsound
= .5 D Prms^2 Vsound^2 / P^2 / Gamma^2 (From above)
Prms^2 = 2 Power P^2 Gamma^2 / (4 Pi R^2) / Vsound^3 / D
The sound intensity in decibels as a function of "Power" and "R" is
Dec = Sound pressure level expressed in decibels
= 10 * LogBase10(Prms^2/Pref^2)
= Constant - 2*logBase10(R)

Frequency Wavelength
(Hertz) (meters)
20 15 Lower limit of human frequency sensitivity
41 8.3 Lowest-frequency string on a string bass or bass guitar
65 2.52 Lowest-frequency string on a cello
131 2.52 Lowest-frequency string on a viola
440 .75 The A-string on a violin
660 .75 The E-string on a violin (highest-frequency string)
20000 .016 Upper limit of human hearing

Wall mass per area = m = 161 kg/meter2
Sound frequency = F = 41 Hertz
Soundproofing constant = C = 66 Hertz kg/meter
Sound transmission fraction = Q = C m-1 F-1 = .01 Calculation in the appendix
The lower the value of Q, the more soundproof the wall. If
Q < 1 The formula is valid
Q = 1 Minimum wall mass/area to attenuate sound
Q > 1 The wall does not attenuate sound.
Composition Density Thickness
g/cm3 cm
Bamboo .85 19
Water 1.0 16.1
Stone 2.7 6.0
Concrete 2.7 6.0
Steel 7.9 2.0
Air pressure = P =101300 Pascals
Air density = D = 1.22 kg/meter3
Air adiabatic index = γ = 7/5
Sound speed = V = (Pγ/ρ)½ = 340 meters/second
Wall thickness = X = .01 meters = 1 cm
Wall density = ρ = 1000 kg/meter3 = 1 grams/cm3
Wall mass/area = m = X ρ = 10 kg/meter2 = 1 grams/cm2
Sound frequency = F = 41 Hertz
Sound input pressure = p1 = .1 Pascals Pressure in the room where the sound is produced
Wall velocity = v =.000039 meters/second
Wall momentum/area = q = m v = p1F-1(2π)-1 = .00039
Sound output pressure = p2 = P v V-1 γ
= p1 m-1 F-1 (2π)-1 P V-1 γ
= p1 m-1 F-1 (2π)-1 P½ D½ γ½
= p1 m-1 F-1 * 66.2
= p1 m-1 (F/41)-1 * 1.61
= p1 (m/m0)-1 (F/41)-1
Wall critical mass/area = m0 = F0 (2π)-1 P½ D½ γ-½ = 1.61 kg/meter2


1861 Reis develops the first speaker capable of reproducing human speech
1876 Bell advances the technology of microphones and speakers, making possible
the first practical telephone.
1877 Edison invents the phonograph, the first device capable of recording sound
and reproducing sound
1888 First known example of a recording of a musical performance
1982 Development of digital music storage (the compact disc)
1890 Berliner develops the disk phonograph. Previous phonographs were cylindrical
1915 Jensen and Pridham build the first moving-coil (dynamic) loudspeaker
x = Displacement of the loudspeaker membrane
v = Velocity of the loudspeaker membrane
A = Loudspeaker vibration amplitude
(The loudspeaker membranes oscillates back and forth between +A and -A)
F = Frequency of the loudspeaker vibration.
t = Time
The position of the membrane as a function of time is
x = A sin(2 Pi F t)
v = 2 Pi A F cos(2 Pi F t)
The velocity of the membrane has magnitude 2 Pi A F.
Vrms = Velocity fluctuation
Prms = Pressure fluctuation
Drms = Density fluctuation
V = Speed of sound
= 340 meters/second
P = Atmospheric pressure
= 101000 Pascals
Gamma = 7/5 for air
Vrms / Vsound = Drms / Dsound
Prms / P = Gamma Vrms / Vsound
= Gamma Drms / D
For example, a loud sound has a pressure fluction on order of 1 Pascal.
Prms/P ~ Vrms/V ~ Drms/D
Prms ~ 1 Pascal
Vrms ~ .003 meters/second
Drms ~ 10^(-5) kg/meter^3
If the sound has a frequency of F=100 Hertz then the speaker amplitude is
A = Vrms / (2 Pi F)
~ .000005 meters
X = Size of a speaker
x = Displacement of the speaker diaphragm while producing sound
F = Frequency of the oscillation
T = Time for one oscillation
= 1/F
V = Characteristic velocity of the diaphragm while producing sound
= x/T
E = Energy produced by the speaker during one oscillation
P = Power produced by the speaker
= E/T
D = Density of air
Z = Dimensionless number characterizing the amplitude of speaker motion
= x/X
When the speaker moves the volume of air affected is of order X^3.
E = D V^2 X^3
The power produced by the speaker is
Power = E/T
= D V^2 X^3 / T
= D x^2 X^3 / T^3
= D (x/X)^2 X^5 F^3
x/X is a dimensionless number that is similar for speakers of different sizes.
Generally it is less than 0.1.
D = Density of air
= 1.2 kg/m^3
x/X = .1
X = .1 meters
F = 100 Hertz
P ~ .1 Watts
If F were increased to 1000 Hertz then this speaker could generate 100 Watts.
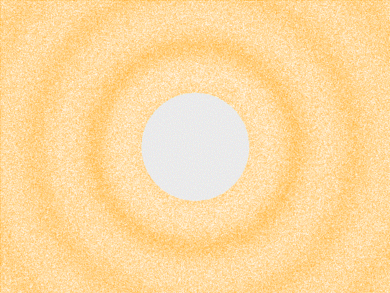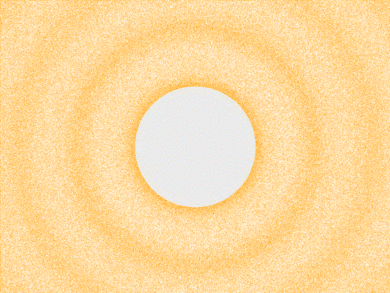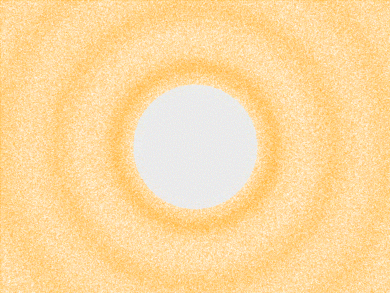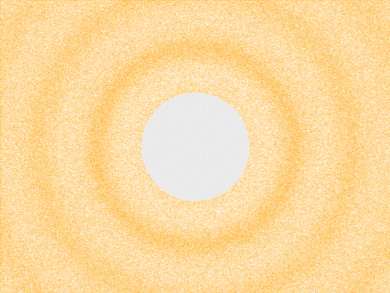
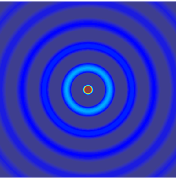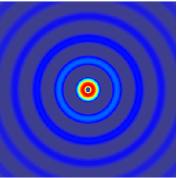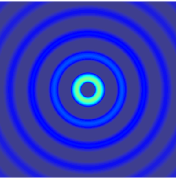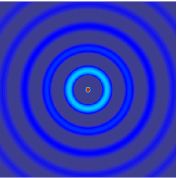
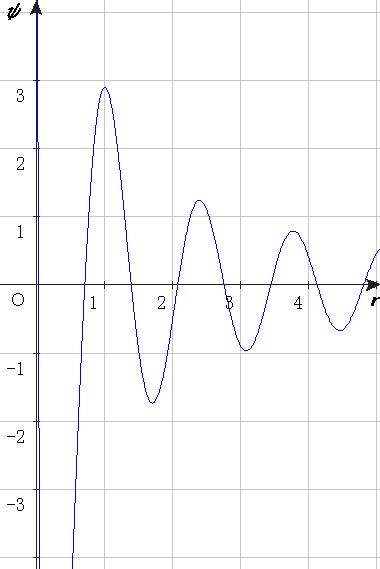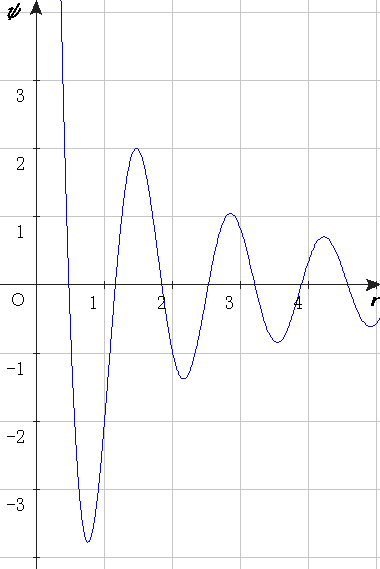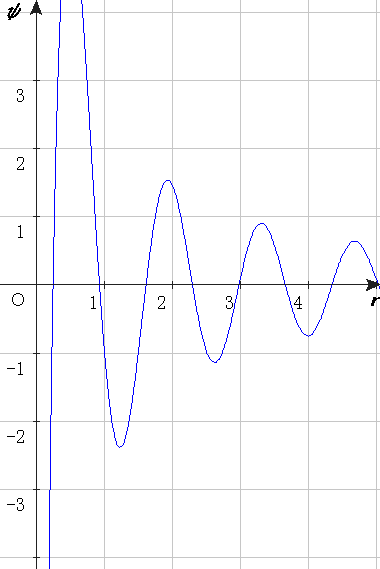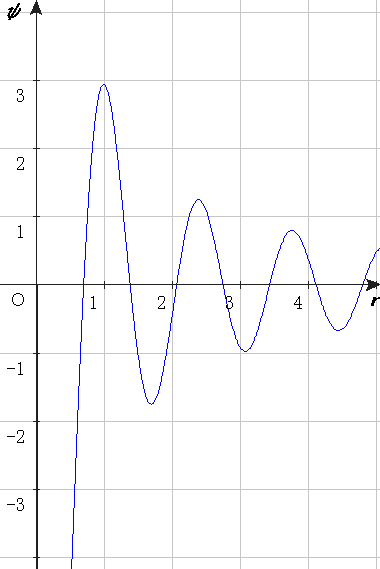
16) Draw a diagram showing how the resonance curve behaves as a function of
the quality parameter.
E = 440 * (3/2) = 660 Hertz
A = 440 = 440
D = 440 / (3/2) = 293
G = 440 / (3/2)^2 = 196
String overtone frequency = N * 440 where N = {1,2,3,4,5,...}
Oboe overtone frequency = N * 440 where N = {1,3,5,...}
D-major: D, E, F#, G, A, B, C#, D
D-minor: D, E, F , G, A, Bb, C, D
Fa = Frequency of the open A-string
= 110 Hertz
Fd = Frequency of the D
= Fa * 2^(5/12)
= 146.8 Hertz
Fe = Frequency of the E
= Fa * 2^(7/12)
= 164.8 Hertz
T = Wave period
La = Length of the open A-string
= .65 meters
V = Speed of a wave on the A-string
= 2 La / T
= 2 La F
= 2 * .65 * 110
= 143 meters/second
Ld = Distance from the D fret to the bridge
= V / (2 Fd)
= La F / Fd
= La 2^(-5/12)
= .487 meters
Le = Distance from the E fret to the bridge
= V / (2 Fe)
= La F / Fd
= La 2^(-7/12)
= .434 meters
Distance between the B and C frets = Le - Ld = .487 - .434 = .053 meters
F = Original frequency
= 440 Hertz
Fwidth = Characteristic width for frequency perception at a frequency of F
R = Charactistic frequency ratio for frequency perception
= Fwidth / F
Suppose you start with a frequency of "F" and slowly change it to a different
frequency "f".
If |f-F| < Fwidth then "f" sounds the same as "F"
If |f-F| > Fwidth then "f" sounds different from "F"
Conduct an experiment to measure the value of R for a range of frequencies F,
and describe the experiment. This isn't intended to be a high-precision measurement.
Any estimation will do.
F = Frequency of the violin string
f = Frequency of the synthesizer
Fwidth = Characteristic frequency width for resonance
R = Characteristic frequency ratio for resonance
= Fwidth / F
If |f-F| < Fwidth then the string vibrates
If |f-F| > Fwidth then the string doesn't vibrate
Conduct an experiment to measure the value of R for a range of frequencies F,
and describe the experiment. This isn't intended to be a high-precision
measurement. Any estimation will do.
© Jason Maron, all rights reserved.